1.位错的应变能与线张力

与理想无缺陷晶格中的原子相比，位错附近的原子偏离了理想晶格中的平衡位置，这会导致位错区域的点阵产生畸变、晶体能量上升，增加的能量称为应变能或畸变能。晶体的总应变能Et可表示为

式中，Ec为位错芯处原子严重错排引起的畸变能；Ee为位错芯外的原子微小位移引起的弹性能。由于位错在运动或与其他缺陷产生作用时，只有Ee发生变化而影响晶体的力学行为，并且弹性力学只能计算Ee，因此位错应变能常常重点关注弹性能这一项。

设一圆柱形晶体存在单一位错，沿其轴向有长度为l的位错，其弹性能Ee可通过积分得出：

其中C′为常数，通常刃位错的C′比螺位错的要大20%～50%；R为圆柱形晶体的半径；r0为位错芯的“半径”，也就是我们在4.3.3节介绍的位错宽度的1/2；b为Burgers矢量的模；G为剪切模量（且假设晶体是弹性各向同性）。由式（4-83）可知，当r0→0时，Ee→∞。实际材料中，Ee→∞是不可能的。故在位错芯内，材料的畸变不能用线弹性理论来描述，即Hooke定律不适用（Hooke定律可简写为σ=Eε和τ=Gγ，其中σ为轴向应力，E为弹性模量，ε为轴向应变，τ为剪切应力，G为剪切模量，γ为切应变）。式（4-82）中，位错芯内的畸变能Ec，其估计值为Ee的10%～30%。由此，可通过人为调整或选取位错芯的“半径”r0，把估算出的Ec叠加到Ee中来计算总应变能Et。离子或金属晶体的r0可在（1/4～2）b间选取。

根据式（4-83），我们可了解Ee正比于位错的长度l。因此，为达到能量最低状态，晶体中的位错总是力图缩短其长度，如弯曲的位错趋向于变成直线。这种力图使弯曲位错恢复成直线的力称为恢复力F。为描述位错线的缩短趋势，人们引入了线张力的概念。线张力T是指位错线增加单位长度时弹性能的增量。由此，把式（4-83）对长度l求导后得：

位错数量较多时，单个位错的弹性应变场，其长程部分会消失，则Ee对圆柱形晶体的半径R的选择不太敏感。而且，位错芯的“半径”r0在（1/4～2）b间选取。因此，人们常把R、r0看成是常数。这样，位错的线张力可写成：

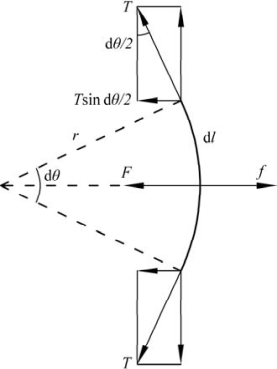
图4.32　位错的线张力T与驱动力f示意图（恢复力F为线张力在平行于驱动力方向的合力）

其中C=为常数。

位错线的恢复力F是由线张力产生的。现在，我们根据线张力来计算Frank-Read位错源所需的剪切应力。假设有一长度为dl的位错线，其曲率半径为r，圆心角为dθ，如图4.32所示。使位错线产生运动的力为驱动力。单位长度的位错线驱动力可表示为f′=τb，则长度为dl的位错线上的驱动力为f=f′dl=τbdl。驱动力与位错线dl相垂直。

而线张力T与位错线是相切的。因此，我们把线张力T分解成与驱动力f平行和垂直的力。与f垂直的线张力相互抵消。与f平行的线张力就是力图使位错线变短、变直的恢复力F，其大小为F=2Tsin（dθ/2）。当dθ很小时，sin（dθ/2）≈dθ/2，则F≈Tdθ。将弧长与弧度的关系dl/r=dθ代入F≈Tdθ中，得到F≈Tdl/r。当恢复力F与驱动力f达到平衡时（即F=f），位错线形状不再改变（这就是我们在位错增殖中提到的“位错线上的受力达到平衡”）。将上述F、f的表达式代入F=f得Tdl/r=τbdl，即τ=T/（br）。再将线张力的表达式（4-85）代入τ=T/（br）中，得到下式：

晶体位错线上的实际剪切应力τ≤τmax时，位错线处于稳定状态；τ＞τmax时，位错线开始扩展，即Frank-Read位错源开始起动。

简单小结一下本节的内容。

（1）位错的应变能与b2成正比（b为Burgers矢量的大小或模）。因此，具有最小Burgers矢量的位错使晶体应变能最低。故滑移总是优先沿晶体中原子的密排面和密排方向产生。

（2）螺位错的弹性能要低于刃位错。

（3）为降低位错引起的应变能，位错线在线张力的作用下有尽量变短、变直的趋势。

由式（4-86），我们可获得位错线移动所需临界剪切应力。由Schmid定律（4.3.1节）也可获得晶体发生宏观塑性变形所需的临界分切应力τc。这两个临界分切应力从不同角度描述了晶体要发生滑移所需的应力。由Frank-Read位错增殖机制我们知道，Frank-Read位错源产生的许多位错环引起大量滑移。这些滑移在宏观上表现为塑性变形。然而，无论是位错线移动的剪切应力，还是由Schmid定律得出的应力，人们在推导它们时都是把晶体当成是连续介质来处理的。

对于连续介质，我们可用弹性理论进行处理。但是，如前所述，我们不能用线弹性理论来处理位错的中心部分。因此，对于位错的中心部分，我们不能把它当成是连续介质，而是要用离散的原子点阵模型来处理。与化工、机械等学科不同，材料科学与工程学科更注重在原子、晶体点阵结构层次处理材料。下面介绍位错离散模型的一些结论。

2.位错的起动力

1940年代，Rudolf Ernst Peierls（1907—1995年）和Reginald Nunes Nabarro（1916—2006年）把晶体分为滑移面上、下两部分。这两部分紧邻滑移面处的相互作用不能用Hooke定律来处理。其余部分可看作是连续弹性体，可用Hooke定律对其处理，所以Peierls和Nabarro的点阵模型是部分离散模型。虽然滑移面上、下原子错位，但仍有相互作用。因此，这些原子会力图相互接近、向相互对齐的方向移动。由此，Peierls和Nabarro建立模型计算了应变能。

在Peierls和Nabarro的模型中，位错应变能包括三个部分：Et=EA+EB+EAB，其中EA、EB分别为滑移面上、下两部分晶体的弹性能，EAB为位错芯处的错排能。位错芯外的EA、EB可用连续介质的弹性理论求出，方法同上一小节，得

式中，ν为泊松比；1/［4π（1-ν）］即式（4-84）中的刃位错的常数C′。对螺位错而言C′为1/（4π）。式（4-87）中，采用位错半宽ζ代替了式（4-84）中数值不确定的位错芯“半径”r0。位错芯区域定义为（-ζ，ζ），在此区域内，原子键合的畸变程度大，线弹性理论失效。2ζ为位错宽度，其值为2ζ=d/（1-ν），其中d为滑移面上、下原子间距，即滑移面面间距。

然而，我们更关心的是位错芯的错排能，因位错的起动与其关系密切。Peierls和Nabarro得出的错排能为

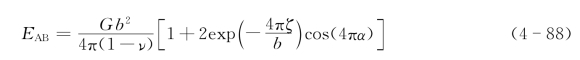
其中α为位错的位置系数，表示位错中心的相对位置（0≤α≤1）。因为位错芯的原子畸变严重，其间距与Burgers矢量不完全相等，所以用αb表示从位错中心到与Burgers矢量等同位置的距离。式（4-88）中的第二项虽然小，但含有位错位置的周期函数cos（4πα）。该函数反映了错配能与位错中心所处的位置关系。而且由于晶体结构的影响，位错能量是位错线位置的周期函数。故位错线在运动时要周期性地经历能峰与能谷。这就需要施加一定的作用力，位错线才能越过这些能峰或势垒。这种作用力可用错排能对位置求导得到：

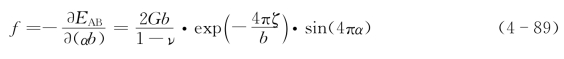
当sin（4πα）=1时，作用力f达到极大值：

于是单位长度的位错产生滑移所需临界剪切应力为：

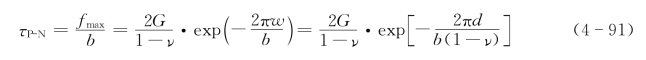
其中w=2ζ即位错宽度，并将2ζ=d/（1-ν）取代w后，得到上式最后一项。τP-N也叫Peierls-Nabarro力（即P-N力）或位错起动力，该力表明了晶格因周期性而对位错产生了阻力，故P-N力也称为晶格阻力。位错要起动，首先要克服晶格阻力。

根据以上分析及式（4-91），可得出以下一些主要结论。

（1）位错的起动力τPN与晶体开始宏观塑性变形相对应。因此τP-N本质上是晶体开始滑移的临界分切应力τc。但由于它们是从不同角度获得的，数值上会有些差异。

（2）位错宽度w不同，起动力τPN也不同。w小，位错宽度窄，则位错的起动力大。一般金属的位错较宽，共价晶体和共价成分较强的晶体中的位错较窄。因此，金属位错的起动力τP-N小，塑性好，共价晶体塑性差。在金属晶体中，bcc金属的位错宽度一般比fcc金属的位错宽度小，τP-N大，故bcc晶体易产生滑移。

（3）滑移面的晶面间距d大，起动力τP-N小，易滑移。因晶体结构中密排面的面间距d大，Burgers矢量b小，所以b/d为最小时，τP-N达到最小，滑移容易优先在该滑移系统发生。

（4）剪切模量G还受温度的影响。温度越高，G减小，故起动力τP-N也减小，滑移容易发生。所以离子晶体、共价晶体在高温下也有一定的塑性。由此，我们还可知道晶体的强度与温度有关。这可能是bcc金属具有确定的塑性-脆性转变温度的一个原因。

不仅位错能使晶体局部发生畸变、产生应力场，晶体中的点缺陷同样也会使晶格产生畸变和应力场，而且晶体中总是存在点缺陷。所以位错在起动时或在运动中都会遇到点缺陷。当这两种缺陷的应力场相遇时就会产生弹性交互作用。

3.位错与溶质原子的作用

（1）位错与溶质原子的交互作用能

假设点缺陷可看作是由一个半径为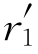的小球填入晶体中半径为r1的球形空洞形成的。这就相当于将一个溶质原子挤入晶体中的间隙位或某一晶格位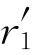，表示点缺陷半径，r1表示点阵间隙的半径或原子半径。以此方式引入一个点缺陷后，晶体局部体积发生变化，用ΔV表示这种变化ΔV≈4πδ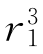，其中δ为错配度，δ=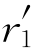（-r1）/r1。球形空洞类似于晶体表面，刃位错垂直于空洞球面。这样，只要正应力在x，y，z轴上的分量在做功。这些正应力的平均值即是在点缺陷处产生静水压力p。当点缺陷处的晶体体积发生变化时，静水压力p所做的功就为点缺陷与位错的交互作用能ΔE=pΔV。为计算静水压力p，需要把根据弹性力学得出的刃位错位错芯外的应力场表达式代入p中。然后经整理并转换成极坐标，得到位错与溶质原子的交互作用能：

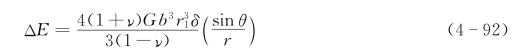
式中，ν为泊松比；G为剪切模量；b为Burgers矢量的大小；θ，r为极坐标中的坐标参数。如果考虑到溶质原子不是刚性球，则交互作用能变为ΔE′：

无论溶质原子是不是刚性球，要使其处于稳定位置，它与位错的交互作用能都应为负。

当体积变化ΔV≈4πδ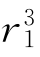＞0时，错配度δ=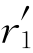（-r1）/r1＞0，即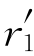＞r1。要使交互作用能ΔE＜0，只有sinθ＜0，即π＜θ＜2π。这表明比基体原子大的置换式或间隙式溶质原子应处于刃位错张应力膨胀部分，即正刃位错的滑移面下半部分。

当体积变化ΔV≈4πδ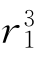＜0时，错配度δ=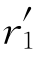-r1）/r1＜0，即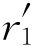＜r1。要使交互作用能ΔE＜0，只有sinθ＞0，即0＜θ＜π。这表明比基体原子小的置换式或间隙式溶质原子应处于刃位错压应力收缩部分，即正刃位错的滑移面上半部分。(www.daowen.com)

（2）柯垂尔气团

根据以上分析，我们可知点缺陷会择优分布于刃位错的某些部位，以使交互作用能达到最低、系统稳定。正因如此，位错附近的点缺陷浓度与晶体中的其他地方有所不同。根据Boltzmann分布律，在交互作用能为ΔE的地方，点缺陷的浓度c可表示为

由式（4-92）或式（4-93）得，在ΔE＜0的范围内，r越小，ΔE的代数值越小，-ΔE越大且是正值，则点缺陷的浓度c增大，故靠近位错的地方（r小），溶质原子多，点缺陷浓度大。

云集于位错附近的这些原子形成溶质原子云或溶质原子气团。比如，α-Fe中常固溶有C、N间隙原子。在温度、时间比较充分的条件下，C、N原子向位错附近的膨胀区聚集，形成C、N原子云，这称为Cottrell气团（Cottrell atmospheres）。当温度下降时，位错附近点缺陷的浓度c很大［见式（4-94）］。在位错中心的全部点阵位置或间隙位置可能被溶质原子所饱和。溶质原子聚集在位错线上形成饱和柯垂尔气团。2000年，牛津大学的J.Wilde等用原子探针直接观察到了钢中环绕位错线的碳原子“气团”。

根据点缺陷与位错的交互作用能、点缺陷在位错的择优分布及Cottrell气团的形成，我们可知：点缺陷的应力场与位错的应力场在一定条件下产生的作用可以使系统的能量处于较低状态。如果我们要使点缺陷与位错分离，必然要对其做功。比如，具有Cottrell气团的位错要运动而离开溶质原子，则会使系统能量升高。这就相当于溶质原子对位错有阻力。因此Cottrell气团有“钉扎”位错、阻滞位错运动的能力。位错不易运动在宏观上显示为晶体的塑性变形难、强度增加。这方面最典型的例子就是bcc金属的明显屈服点现象。

图4.33示意了fcc、hcp和bcc金属的应力σ-应变ε曲线。图4.33（a）为fcc和hcp金属，也是常见的σ-ε曲线。Ⅰ为符合Hooke的弹性变形区；Ⅱ为过渡区，晶体的硬化速率不断下降；Ⅲ为线性硬化区，应变硬化速率恒定；Ⅳ为抛物线硬化区。图4.33（b）为bcc晶体（如退火低碳钢）的σ-ε曲线，它明显与fcc和hcp的不同。bcc晶体σ-ε曲线的显著特点是有明显的屈服点（即在该处有明显塑形变形）。当应力低于图4.33（b）中b点对应的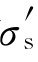时，试样产生弹性变形；当应力达到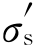时，试样变形所需应力迅速减小到下屈服点σs。此时，应力不再增加，仅有微小波动。但应变却在应力几乎不变的情况下继续增加，材料暂时失去抵抗变形的能力，并一直持续到c点。这种具有明显屈服点的塑性流动现象即是上文提到的明显屈服点现象。这种现象与材料的纯度、温度等有关系。比如，极纯的α-Fe在拉伸时并无明显屈服现象。但含有微量C、N杂质的α-Fe却有明显屈服现象出现，而且，温度升高，该现象要消失。这种明显屈服点现象是Alan Howard Cottrell（1919-2012年）在1940年代末期对低碳钢试样做拉伸时发现的。如何解释这种现象呢？Cottrell受Orowan和Nabarro位错理论的影响提出了Cottrell气团学说并对此做了解释。

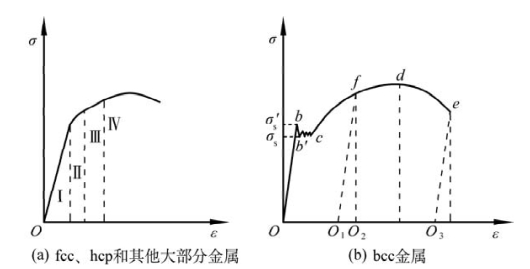
图4.33　典型金属的应力应变曲线（引自潘金生，2011）

体心立方（bcc）金属中的C、N间隙原子在位错附近形成Cottrell气团，将位错“钉扎”住。当σ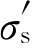＜时，位错不能起动，因此不能产生塑性变形，而只产生弹性变形；当σ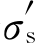＞时，位错与气团中的间隙原子脱离而成为自由位错，位错可运动并产生塑性变形。而自由位错因没有点缺陷应力场的牵制，在较低应力下就可运动，所以变形所需应力迅速减小到下屈服点σs。

然而，当低碳钢在下屈服点产生变形后，卸载停止实验，并把试样在室温下停放一段时间。Cottrell发现，再次拉伸时，低碳钢试样的屈服点随卸载停放时间的增加而提高，即低碳钢发生了强化或应变时效（strain age）。Cottrell当初发现这种现象后，还不能很好地解释。后来，他提出的Cottrell气团学说不仅能很好地解释前述的明显屈服现象，还能解释应变时效。

低碳钢试样在第一次拉伸时，位错脱离间隙原子（即脱钉）而产生塑性变形。卸载后，间隙原子要通过扩散才能重新与位错结合成气团。若停留较短时间，则间隙原子来不及扩散到位错线周围，Cottrell气团未充分形成。这时的位错没有受到很大的气团阻力，在较小应力作用下就可运动。因此，试样可在低应力（σs）下产生屈服。反之，若停留时间较长，则间隙原子有充裕的时间重新扩散到位错线周围（因为它们的结合有利于系统能量的降低），形成Cottrell气团。气团重新将位错“钉扎”住，阻滞位错运动。此时，位错只有在更高应力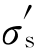（）下才能运动，也就是样品的强度、硬度提高了，得到了强化即应变时效。Cottrell曾预言：C原子重新进入气团的量与t2/3成正比（t为应变时效的时间）。这个预言得到了证实。如果试样停留时所处的环境温度较高，则间隙原子易扩散。Cottrell气团形成的时间短，即较高温度下，停留较短时间也会出现应变时效。

通过对Cottrell气团的分析，我们可知，要形成稳定的Cottrell气团和由此引起的明显屈服与应变时效现象，对温度有一定要求。温度太低，间隙原子扩散慢，Cottrell气团较难形成；温度太高，间隙原子能量高，又容易脱离Cottrell气团。在这两种情况中，Cottrell气团对位错都起不到“钉扎”作用，所以温度要适宜。

以上主要是bcc金属晶体中的明显屈服现象。那fcc晶体又如何呢？在“位错起动力”小节，我们已经知道，fcc晶体中的位错起动力τP-N小于bcc晶体的τP-N。而且开始时，可动位错的密度较大，间隙原子对位错的“钉扎”作用弱。因此，fcc晶体通常无明显的屈服现象。但由于其他原因，一些金属和合金（含fcc金属的合金）也会出现明显的屈服现象。

在本小节对Cottrell气团的介绍中，我们主要针对刃位错与间隙原子的作用。实际上，螺位错与间隙原子也存在相互作用。但间隙原子与螺位错间的作用要比它与刃位错间的作用弱得多。对此，我们不做进一步介绍。

位错不仅与点缺陷有相互作用，位错间同样存在相互作用。因每个位错周围都存在一定的应力场，所以每个位错的应力场与邻近位错的应力场也会相互影响、相互作用。

4.位错间的相互作用

在众多相互作用的位错中，平行位错间的相互作用最简单，且各处相同。两平行螺位错的相互作用力可表示为

式中，b1，b2为Burgers矢量的数值大小；r为两螺位错的间距；G为剪切模量。两同号螺位错相互作用时，Fr＞0，即它们相互排斥；两异号螺位错相互作用时，Fr＜0，它们相互吸引。若两个螺位错都可自由移动，则它们要么相互排斥至无穷远，要么相互吸引合并而消失。图4.30（d）中的m、n段为异号螺位错，所以它们相遇后相互抵消，使位错线断裂成封闭位错环和环内折线。

对于两个平行刃位错e1，e2（图4.34）。假设它们的位错线平行于z轴，Burgers矢量b1，b2都平行于x轴，而且e1、e2的滑移面都平行于xOz面。令位错e1在坐标原点O，则导致e2沿x轴方向的滑移力Fx和沿y轴的攀移力Fy分别为

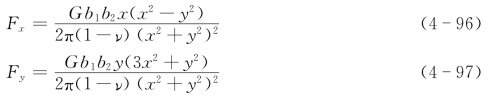
若刃位错e1，e2同号，如图4.34（a）所示，则：

（1）图中的θ在［0，π/4）、（3π/4，5π/4）及（7π/4，2π］的区域内，|x|＞|y|，（x2-y2）＞0。根据式（4-96），在［0，π/4）和（7π/4，2π］区域内，x＞0，故x（x2-y2）＞0，所以Fx＞0；在（3π/4，5π/4）的区域内，x＜0，故x（x2-y2）＜0，所以Fx＜0。此处Fx的正负是指Fx指向x的正方向或负方向，这与位错正负的意义有所不同。图4.34（a）中，位错e2在［0，π/4）和（7π/4，2π］区域内，它的受力方向指向x轴正方向；在（3π/4，5π/4）区域的e2，其受力方向值指向x轴负方向。也就是说，与坐标原点e1同号的位错e2在这两个区域，它们要相互排斥而远离。

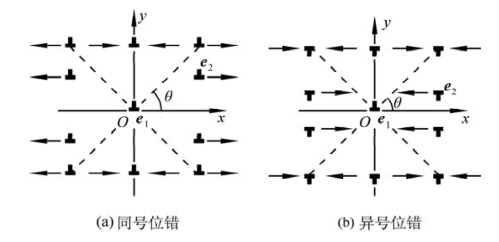
图4.34　两平行刃位错在x轴方向上的相互作用（图中水平箭头表示受力方向，虚线为x、y轴夹角平分线）（引自蔡珣，2010）

（2）图4.34（a）中的θ在（π/4，3π/4）、（5π/4，7π/4）的区域内，|x|＜|y|。当x＞0时，（x2-y2）＜0，据式（4-97），Fx＜0，所以位错e2的受力方向指向x轴的负方向；x＜0时，同样有（x2-y2）＜0，所以Fx＞0，位错e2的受力方向指向x轴的正方向。因此，在这两个区域且与坐标原点e1同号的位错e2相互吸引。

（3）当x=0时，e2位错在y轴上，Fx=0，位错处于平衡状态。也就是说，与原点处的e1同号的位错e2一旦偏离y轴，就会受到e1的吸引又回到y轴。因此在|x|＜|y|区域中的位错有向y轴移动的趋势。当这些位错在y轴上竖直排列起来时就形成了位错墙。位错墙可构成面缺陷的一种——小角度晶界。

（4）当|x|=|y|时，即e2位错在图中的虚线上。此时的e2位错处于亚稳态。它一旦偏离该平衡位置，要么被同号的e1排斥，要么被e1吸引到y轴上达到稳定态。

（5）当y=0时，即e2位错在x轴上，此时e1、e2总是相互排斥的。它们相距越近，排斥力越大，所以处于同一滑移面上的同号位错总是相互排斥的。

（6）攀移力Fy与y同号。y＞0时，攀移力指向y轴正方向；y＜0时，攀移力指向y轴负方向。也就是两同号位错在y轴上相互排斥。

以上（1）～（6）点讨论了同号刃位错间的作用力。对于异号位错，它们的受力与同号位错恰好相反，如图4.34（b）所示。请读者自行分析。

纯螺位错与纯刃位错的Burgers矢量相互垂直，它们的点积为b1·b2=0。故它们彼此不发生相互作用。对于混合位错，要分解成刃型和螺型分量，再分别考虑它们之间的作用力。

在晶体的表面，晶体的周期性中断、表面原子受力不均衡、原子位置要做调整。因此，表面也存在应力场。当位错运动到表面附近时，它们之间也存在一定的相互作用。

5.位错与自由表面的相互作用

在位错的应变能一节，我们给出了位错弹性能的表达式（4-83）。设位错芯的“半径”r0不变，而圆柱形晶体的半径R减小（这相当于位错离晶体表面的距离在缩小，或者说位错在向晶体表面移动）。这时，由式（4-83）位错的弹性能Ee减小。因此，晶体表面以下的位错，尤其是近表面位错，有向表面移动的趋势以降低系统应变能。这好像有一种力将位错拉向表面一样。为此，人们提出一种虚构的力——镜像力来描述自由表面对位错的作用。

镜像力使近表面位错力图移到表面，而且这些位错与自由表面有正交的倾向。又因Burgers矢量的连续性，位错线如果不是以位错环的形式存在，则要起止于单晶体表面。在腐蚀剂的作用下，这些在表面露头的位错容易被腐蚀而形成蚀坑。在位错密度一节，我们已经介绍过，测定蚀坑数可获得位错密度。此外，因表面的位错密度大，表面的硬度也较大，这会赋予晶体表面较强的耐磨性。

为什么位错密度大，硬度也较大？在位错的运动一节，我们明白了推动位错所需外力不是很大。故晶体的实际切变强度要远小于理论切变强度。如果这样的话，位错越多，那晶体不就越容易发生塑性变形吗？当然，现在我们可以用Cottrell气团、位错间的作用力对其做解释。除了这些解释以外，当很多位错拥挤在一起时，又会有哪些现象发生呢？

6.位错的塞积

根据位错的交滑移增殖机制，我们了解了位错在运动过程中可能会遇到障碍物。这些障碍物可能是沉淀相、晶粒边界、第二相粒子及固定位错等。

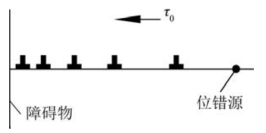
图4.35　位错塞积示意图（τ0为外力在滑移方向的分切应力）

以Frank-Read源为例，在外力作用下，位错环不断产生。这些由同一位错源产生的位错在同一滑移面上运动，并向周围扩散开。最先遇到障碍物的位错称为领先位错。领先位错遇到障碍物的阻碍而停下来。后面的位错因位错间的斥力（它们在同一滑移面上，要么合并消失，要么产生斥力，如图4.34所示），也受到阻碍而停止运动，这称为位错的塞积（dislocation blocking），如图4.35所示。塞积在一起的位错称为位错塞积群。

塞积群中的每一个位错不仅受到外力场的作用，还受到位错应力场的作用。根据这两种力的平衡，可求出每个位错的位置：

式中，xi为从障碍物开始计算的第i个位错距障碍物的距离；k为常数（螺位错k=1，刃位错k=1-ν）；n为塞积群中的位错数目；τ0为外力在滑移方向的分切应力；G、b分别是剪切模量和Burgers矢量的数值大小。把式（4-98）变换一下，得

由式（4-99）可知，距离障碍物越近（即xi越小），则位错的数目n越大。越靠近障碍物，位错间距越小，所以塞积群中，位错的分布是不均匀的。

另一方面，障碍物对塞积群的作用，常被认为是近程作用。离障碍物越远，应力迅速下降，所以障碍物对领先位错的作用可被认为是对塞积群的作用。塞积群中，每个位错的受力可表示为τ0b，n个位错的受力一共为nτ0b。而障碍物对领先位错的作用力τ与τ0的方向相反，大小为τb。当受力达到平衡时，nτ0b=τb。化简后为

式（4-100）表明，在塞积群中，障碍物在领先位错前端产生很大的应力，其数值为外加剪切应力τ0的n倍。当塞积群中的位错数目n增加，领先位错前端的应力τ不断增大。当τ增大到一定程度时，塞积群中的螺位错通过交滑移越过障碍。τ继续增加，甚至可把障碍物摧毁。如果障碍物为晶粒边界，当τ达到一定数值时，可诱发相邻晶粒中的位错源开动。这会导致位错运动从一个晶粒传播到另一个晶粒。

小结一下位错塞积的主要影响：①使Frank-Read源开动所需应力大大增加。按式（4-100），应力要增加n倍。这是材料产生加工硬化的原因之一。②若塞积的位错为刃位错，则当位错数目足够大时会出现微裂纹。③若障碍物为晶界，则位错塞积可能会使邻近晶粒中的位错开动，产生塑性变形。④若障碍物为沉淀颗粒，螺型位错可发生交滑移；刃位错可在较高温度下发生攀移。交滑移和攀移可使位错的塞积应力下降，晶体发生软化。