滑移是指在剪应力（shear stress）作用下，晶体相邻的两部分沿着一定的晶面和晶向产生相对滑动。产生相对滑动的相邻两部分间的交界面称为滑移面（glide plane）。滑移的结果是在晶体表面形成许多小台阶，称为滑移带。台阶之间的线条称为滑移线，亦即滑移面与未滑移区或晶体表面的交线，如图4.11所示。

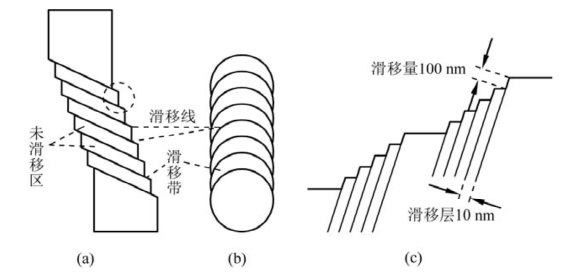
图4.11　单晶金属圆棒试样拉伸后的自由滑移变形示意图

［（a）宏观模型；（b）为（a）的俯视图；（c）为（a）中圆圈区域的放大示意图。为使图清晰，我们使（b）（c）与（a）的比例有所不同。图4.11（a）中的倾斜平行线为滑移带，在电子显微镜下它由一系列平行线组成，即图4.11（c）中构成滑移层的细平行实线。这些细平行实线实际上是滑移面在二维图上的投影，也即图4.11（c）中的细平行实线表示滑移面。根据（潘金生，2011）和（蔡珣，2010）画出］

滑移是在剪切应力的作用下产生的。那在某个面上产生滑移，最小需要施加多大的剪切应力呢？剪切应力是指作用在单位滑移面面积上的力，且该力的方向与滑移面的法线方向正交，即力的方向与滑移面平行。如果剪切应力均匀地分布在滑移面（或剪切面）上，则名义剪切应力τ可表示为τ=F/A，其中F为作用在滑移面上的作用力，A为滑移面面积。每个滑移面有最大能承受的剪切应力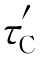。当实际产生的剪切应力达到甚至超过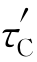时，滑移就产生了。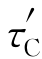称为临界剪切应力（critical shear stress），不同的滑移面、滑移方向，其临界剪切应力不同。下面对此做一推导。

图4.12　圆柱形单晶滑移面上剪应力的确定（n为滑移面法线矢量，b为滑移方向的矢量）（引自关振铎，2011）

设一横截面面积为A0的圆柱形单晶受轴向拉力F0的作用，如图4.12所示。φ为某个滑移面的法线与外力F0方向的夹角；λ为滑移方向（glide direction）与外力F0方向的夹角。根据名义剪切应力的定义，要分别求出作用在滑移面上的作用力F和滑移面面积A。由图4.12可知，滑移面面积A=A0/cosφ，平行于滑移面的力F=F0cosλ，故在此滑移面上的名义剪切应力为

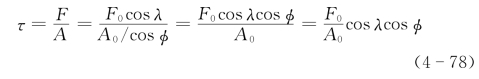
式中，F0/A0为作用在圆柱形单晶轴向的拉应力，常用σ表示。故上式可写作：(www.daowen.com)

τ是轴向应力σ在滑移方向上的剪切应力分量，故也叫分切应力（resolved shear stress）。

物理学家Erich Schmid（1896—1983年）发现同种材料但不同取向的单晶试棒在拉伸时，它们开始滑移的分切应力都相同。1935年，他和冶金学家Walter Moritz Boas（1904—1982年）一起在他们出版的一本书中论述了这方面的问题。人们把式（4-79）称为Schmid定律（Schmid's Law）。

滑移现象表明：塑性变形在晶体中呈不均匀分布（与λ、φ有关）。滑移只在部分晶面产生。在一个晶面，滑移是逐步进行的。滑移总是沿原子密度大的晶面和晶向发生。原子密度大的晶面其晶面间距大，点阵阻力小，容易在这些面上发生滑移。在原子堆积密度大的方向，原子间距最短，只要移动较小距离，就能找到平衡位置，因此也容易在这些方向产生滑移。滑移面和滑移方向一起称为滑移系统。fcc结构的Cu，其｛111｝面和＜110＞方向为常见的滑移系统。滑移系统多，可能的滑移取向也多，滑移容易发生，晶体易变形，即塑性好。金属的滑移系统比较多，如bcc结构的Fe，其滑移系统有48种之多。而无机非金属的滑移系统很少，所以金属的塑性往往要优于无机非金属的。但随着温度的升高，滑移系统可能增多，比如Al2O3在高温下有滑移现象产生。金属铝在高温下还可能出现｛001｝和＜110＞组成的滑移系统。

下面对Schmid定律做一些讨论。

（1）首先发生滑移的系统，其分切应力τ大于该滑移系统的临界分切应力τC。

由Schmid定律τ=σcosλcosφ，我们可获得某个滑移系统的τc。在受拉力初期，可把外力F0和单晶截面积A0看作不变，则拉应力σ不变。那么分切应力τ就与方向有关，即与cosλcosφ值有关。在确定的滑移面上，φ值是固定的。平行于滑移面的分切应力有很多方向，只有λ与φ在同一个平面内时，λ最小，cosλ值才达到最大。也即λ+φ=90°时，该方向的分切应力最大。当该分切应力达到甚至超过该滑移系统的临界值τC时，滑移现象产生。

（2）多滑移。

若一个晶体具有两个或两个以上的滑移系统，它们的cosλcosφ值相同，则必有多个滑移系统同时开动，产生双滑移、多滑移甚至交滑移。晶体在滑移变形时，晶面还会发生转动，这会导致另一些滑移面上的分切应力逐渐增加，甚至超过其临界值，所以随着滑移的进行，滑移系统可能会增加。

根据完整晶体模型，可计算出单晶体产生塑性形变所需的临界分切应力τC，其值约为G/30，其中G为晶体的切变模量（或剪切模量）。但是，实验测得实际晶体的屈服强度要比G/30低3～4个数量级。为何相差这么大？为解释这种差异，许多人都提出了各自的解释。