固溶体中存在多种点缺陷：置换原子、间隙原子、空位。通过对其影响因素的评估，我们可以初步判断一个系统是否能形成固溶体，以及固溶体的组成范围和结构。若系统完全处于热力学平衡态，则固溶体的形成可以参考相图来分析（请参阅本书第8章）。但由此得出的结论是否正确，以及实际固溶体中究竟是哪种点缺陷，还无法从热力学上做出准确判断，更多是由实验来确定的。

无论哪种类型的固溶体，都会引起材料结构和性能的变化，故我们可以通过X射线衍射（XRD）、电子衍射等方法来测定固溶体晶胞参数、点阵类型及组分。我们还可用热分析等方法来了解固溶体性质的变化。这方面的内容请结合后续课程《材料现代分析方法》进一步学习。我们在此重点介绍常用的密度对比法。

1.金属基固溶体

首先用XRD等方法测出固溶体的点阵常数和主晶相的晶体结构类型。根据结构类型和点阵常数，我们可以得出纯主晶相一个晶胞中的原子数Z和晶胞体积V，如3.5.1节介绍的Cu，属fcc结构，每个晶胞有4个铜原子，即Z=4；晶格常数a=3.61Å。据此，读者应该能算出一个Cu晶胞的体积。再由下式算出主晶相的理论密度ρ0（g/cm3）：

式中，L为阿伏伽德罗常数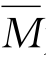为固溶体平均摩尔质量（g/mol）。另一方面，通过实验直接测出对应固溶体的实际密度ρ。然后，将理论密度与实际密度作对比来判断固溶体类型。

空位型固溶体是指有些点阵上无原子。

在密度计算的基础上，我们还可用固溶体晶胞内的实际原子数Z′与主晶相晶胞内的原子数Z的比值做判断。实际原子数Z′的计算式可由式（4-48）演变而来：

其中ρ为实际密度。

2.金属氧化物固溶体

金属氧化物固溶体类型的密度判别与金属基固溶体相似。不同之处在于，我们先要写出生成不同类型固溶体的缺陷反应方程。根据缺陷方程计算固溶体的理论密度，然后再与实际密度对比。其基本步骤如下。

（1）由XRD等方法获得固溶体的点阵常数和主晶相的结构类型，并算出晶胞体积。立方晶系、四方晶系和六方晶系晶胞的体积比较容易获得：立方晶系V=a3、四方晶系V=a2c和六方晶系V=

（2）写出可能的缺陷反应式，得出固溶体化学式，即固溶式。

（3）根据固溶式计算晶胞质量m：

Z是我们在第3章各结构类型中介绍的每个晶胞中的“分子”数。对于纯金属如Cu，一个晶胞有四个Cu原子，故其原子个数和其“分子”个数相同。而金属氧化物晶体，一个纯主晶相晶胞中的原子数和“分子”数是不同的，如每个MgO晶胞有四个MgO“分子”。

（4）由ρ0=m/V得出固溶体理论密度。

（5）把理论密度ρ0与实际测定的密度ρ做对比。理论密度ρ0与实际密度ρ相近的固溶式是合乎实际的。

该方法也可用于金属基固溶体。实际表明，对于不同类型的固溶体，密度值有很大的不同。用密度对比法可以较准确地确定固溶体的类型。

例4.3 一奥氏体钢固溶体中Mn、C、Fe的质量分数分别是12.30%、1.34%、86.36%。用XRD测得其晶胞参数为0.3624 nm，实验测得其密度为7.83 g/cm3，试判断此固溶体的类型。Mn、C、Fe的相对原子质量分别是54.94、12.01、55.85。

解：奥氏体钢固溶体的主晶相为Cu型结构的γ-Fe，Z=4。请读者自己根据式（4-48）～式（4-51）做判断。这里我们用与金属氧化物固溶体相同的办法来做判断，因为判断金属基固溶体和金属氧化物固溶体类型的方法是统一的。取100 g这种固溶体作基准，其中Mn、C、Fe的物质的量分别是0.224 mol、0.112 mol、1.546 mol。

（1）假设Mn、C都是间隙原子，则γ-Fe晶胞的正常格点上全是Fe原子。我们仿照金属氧化物固溶式的写法写出奥氏体钢的固溶式。铁的化学式Fe1（下标1常被忽略），而且晶胞中的Fe原子没有被置换，故有Fe1MnxCy。根据三者物质的量之比，我们可得出x=0.224/1.546=0.145，y=0.112/1.546=0.072。因此，固溶式为FeMn0.145C0.072。

由晶胞参数得晶胞体积为V=a3=（0.3624×10-7）3=47.6×10-24cm3。由式（4-52）得晶胞质量：

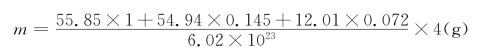(www.daowen.com)

理论密度ρ0为

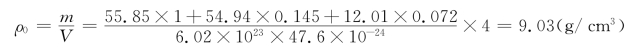
该密度与实际密度7.83 g/cm3相差较大。我们再做第二种假设。

（2）由于Mn原子比C原子大，假设C是间隙原子，而Mn进入正常格点产生置换。设有x个Mn原子置换了Fe，则Fe在化学式中就少了x个，这部分的化学式可表示为Fe1-xMnx。加上间隙位的C，总的固溶式为Fe1-xMnxCy。根据这三者物质的量之比有x/（1-x）=0.224/1.546，得出x=0.127，因为y/x=0.112/0.224，得出y=0.064，故固溶式为Fe0.873Mn0.127C0.064。这种固溶体的理论密度ρ0为

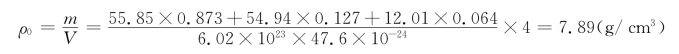
由上述可见，这种情形的理论密度很接近实际密度。如果Mn原子与C原子都进入正常格点，其理论密度又如何呢？

（3）假设Mn、C都进入正常格点产生置换，则γ-Fe晶胞的正常格点由Fe、Mn、C原子所占据。设有x个Mn原子和y个C原子置换了Fe，则Fe在化学式中就少了（x+y）个，固溶式可表示为Fe1-x-yMnxCy。此时的x、y、1-x-y实际就是固溶体中Mn、C、Fe的摩尔分数，其值分别是0.119、0.060、0.821，故固溶式为Fe0.821Mn0.119C0.060。其理论密度ρ0为

把这三种方法获得的密度值与实际测得的密度7.83 g/cm3相比，我们看到第二种假设的密度7.89 g/cm3与实际非常接近。所以题目所给固溶体的类型是C原子进入间隙位，而Mn原子进入晶体正常格点产生置换。

除了这三种情形，Mn也可能进入间隙，C也可能进入正常格点产生置换。用同样的方法，请读者算一下后两种可能固溶体的密度，看看是否与实际密度接近。当然，读者在尝试了式（4-48）～式（4-51）的方法后会发现，对于金属基固溶体，我们例子中的方法比较复杂。但它容易判别哪种原子在间隙位或正常格点位。

例4.4 把摩尔分数为15%的CaO加入立方ZrO2中，在1600℃形成固溶体。实验测得固溶体的晶胞参数为0.513 nm，固溶体密度为5.477 g/cm3，试计算说明固溶体的类型。元素的相对原子质量O=16.00，Ca=40.08，Zr=91.22。

解：立方ZrO2属萤石结构，Z=4。其晶胞体积V=a3=（0.513×10-7）3=1.35×10-22（cm3）。CaO加入立方ZrO2中有两种可能的缺陷反应。

（1）第一种可能的缺陷反应：

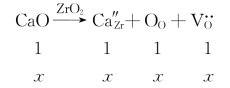
按此反应式，反应物CaO与生成物的物质的量之比为1∶1∶1∶1。每引入1个CaO“分子”，晶胞中就会少1个Zr和1个O，故固溶式可写作Zr1-xCaxO2-x。Ca离子、Zr离子共同占据ZrO2晶胞中Zr离子的位置。根据固溶式中的下角标，我们可知Ca离子在正常晶格中的摩尔分数为x/（1-x+x）。当引入摩尔分数为15%的CaO时，固溶式中的x即为0.15，固溶式为Zr0.85Ca0.15O1.85。根据式（4-52），可计算出这种固溶体的理论密度：

（2）第二种可能的缺陷反应：

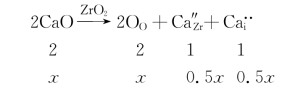
与前种情形类似，每引入1个CaO“分子”，晶胞中就会少0.5个Zr，故其固溶式为Zr1-0.5xCaxO2。引入摩尔分数为15%的CaO时，固溶式中的x为0.15，固溶式变为Zr0.925Ca0.15O2。这种固溶体的理论密度为

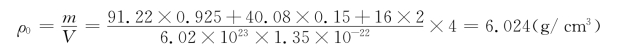
把以上两个理论密度与实际密度5.477 g/cm3相比，我们发现，第一种固溶体的理论密度与实际密度很接近。这说明在1600℃时，形成氧离子空位型固溶体是合乎实际的。但第二种缺陷反应形成的阳离子间隙型固溶体也可形成。图4.7对此做了证实。

图4.7（a）为1600℃时CaO加入立方ZrO2中，两种模型的数据与实际测定的数据做比较。CaO的摩尔分数在5%～25%内，阴离子空位型的数据与实测密度很接近，而与阳离子间隙型的数据相差较大。这说明在1600℃时，固溶体以阴离子空位型存在，即例4.4中的第（1）种缺陷反应。

图4.7　添加CaO形成的ZrO2固溶体密度与CaO摩尔分数的关系（引自Kingery，2010）

图4.7（b）为1800℃时CaO加入立方ZrO2中两种模型的比较。CaO的摩尔分数在5%～15%内，阳离子间隙型的数据与实测值接近；而摩尔分数在20%～25%内，阴离子空位模型的数据与实测密度很接近。这说明：在更高的温度下，掺入较少的CaO还是可以形成阳离子间隙型固溶体的，即例4.4中第（2）种缺陷反应在条件合适时，还是可能发生。这也表明在不同的温度和摩尔分数条件下，固溶体可以有不同类型的形式存在。

我们已重点介绍了本征缺陷、掺杂形成的点缺陷和固溶体。在分析这些缺陷的过程中，我们总认为主晶相和掺杂物服从定比定律。那有没有不符合定比定律的化合物呢？