根据Weiss总结的晶体对称定律，我们知道晶体中可能出现的对称轴只能是2、3、4、6次，不可能存在5次及高于6次的对称轴。

在按照对称要素组合定理推导宏观对称型时，若高次轴Ln、Lm（n、m＞2）多余一个，且相交于一点O，那么在Ln周围必有n个Lm。分别在每个Lm上距O点等距离处取一点，连接这些点，会得到一个正n边形。Ln位于正n边形的面中心，Lm分布于正n边形角顶。每个角顶周围，有m个正n边形围成一个多面角（多面角是指有公共端点并且不在同一平面内的s条射线，s≥3，以及相邻两条射线间的平面部分所组成的图形），所以两个高次轴相交必然产生凸正多面体。立体几何学已证明：一个凸多面体的多面角至少需要三个面构成，且一个多面角角度之和小于360°。因此，围成正多面体的正多边形只能是正三角形（内角60°）、正方形（内角90°）和正五边形（内角108°）。在古希腊时代，就已证明了这些正多边形围成的多面体只有正四面体、正八面体、正方体、五角正十二面体及三角正二十面体五种。按照推导对称型的方法，五角正十二面体和三角正二十面体会出现5次对称轴。这与晶体对称不符而被舍弃。结果，晶体中允许的对称轴组合只有11种。在这11种的基础上，考虑对称面、对称中心，再除去重复的，即得到前文所述的32种宏观对称型或点群。

5次对称轴真的不能出现吗？花瓣不就经常以5次旋转对称轴的形式出现？事实上，晶体中的对称与平移，以及图形是否能密排而不出现空隙有关。读者可能注意到家里的地砖、墙砖，广场上的地砖大都是正六边形、正四边形而不是正五边形铺就。现以正六边形为例说明晶体的平移对称性。

在图2.39（a）所示的晶体二维投影面中，所有的正六边形都具有相同的取向。将正六边形的中心沿着某方向连成一系列虚线。则这些虚线相互平行，且间距相等。若将虚线1上的一串正六边形沿箭头方向平移到另一平行虚线2、3、4或5上时，正六边形完全重合。我们称这种特性为长程平移对称性。

在图2.39（b）中，正五边形具有五次旋转对称性。若用它来铺砌地面，则要么留有空隙，要么图案重叠。我们不可能像图2.39（a）那样通过平移正五边形来将整个平面铺满而不留有空隙。同样，用具有五次旋转对称性结构的正十二面体和正二十面体也不能将整个三维空间填满。在单位平行六面体或晶胞选择一节，我们已知每种晶体是由一种晶胞在三维空间通过平移而毫无间隙地堆砌而成的。而晶体是由许多原子周期性地堆积而成的。如果晶体中的原子不能密排，那图2.39（b）所示的空隙是什么呢？因此，经典晶体学不允许有5次旋转对称性。花瓣有5次旋转对称轴除了基因的因素以外，可能还因为它不需要密排，是一朵朵分开的。

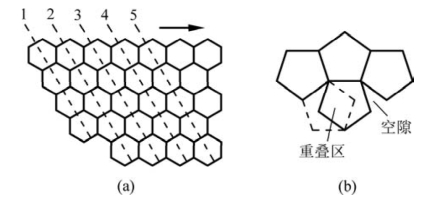
图2.39　（a）晶体的二维平移对称性示意图；（b）准晶的旋转对称性示意图（引自陈波，2012）

平移对称性是经典晶体学的定律，不仅进入了晶体的经典定义，还体现出自然规律的魅力。如果原子堆砌成的物质不需要它满足平移对称性，并且作为结构单元的“晶胞”在一种晶体中有多种而不是一种（以铺满空间而不留空隙），那这种物质就不是经典晶体学中的晶体了。

对晶体平移对称性的第一个冲击来自调制结构。在调制结构中，有一个稳定周期的结构。如图2.40所示，假设该结构在一维方向上的稳定周期为T1=2，每隔2个单位重复一次。另外，由于成分、畸变等原因产生另一种周期，设为T2=3，即每隔3个单位重复一次。T1与T2有公倍数，其最小公倍数是6，所以这两个周期每隔6个单位相遇或重复一次。这样，我们就可以用它们周期的公倍数来描述整个晶体，即晶体具有周期性。但如果T1=1、T2=，那这两个周期的公倍数不是有理数，或者说是不可公度的。因此整个晶体也可能不是周期性的。如MnSi2合金的调制结构，Mn、Si原子在c轴方向的排列周期就是不可公度的。

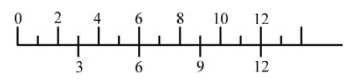
图2.40　一维可公度周期示意图(www.daowen.com)

对晶体平移对称性的第二个冲击来自嵌套在晶体结构中的五次对称单元。1952年，Linus Carl Pauling（1901—1994年）等在确定Mg32（Al，Zn）49的晶体结构时发现了二十面体对称的多壳层结构。1960年代，C.B.Shoemaker在Pauling实验室里测定高合金钢的金属间化合物时，也发现了大量原子处于二十面体中。

对晶体平移对称性的第三个冲击来自研究各种单元无限堆砌的数学晶体学家。1974年，英国数学家Roger Penrose用锐角为36°和72°的两种菱形拼接出了具有5次对称，且无空隙的二维图案（图2.41）。1982年，英国晶体学家Alan Mackay将两种菱面体非周期地堆砌于三维空间，并用准晶格这个词来描述这种有两种长度、有一定规律的图形。Mackay还用实验阐明了准晶格具有明锐的5次对称斑点衍射花样。

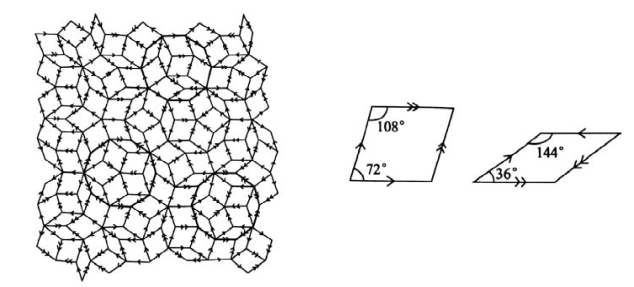
图2.41　两种菱面体按照适配原则生成二维准晶（引自Cahn，2008）

冲破传统晶体学平移周期性观念的关键一步是由以色列材料学家Dan Shechtman完成的。1982年，他在观察Al-Mn合金时发现一种具有二十面体点群对称的合金相。在用电子衍射法分析时，他得到了具有明锐布拉格散射斑的图像。但同事告诉他，这可能是多重孪晶的衍射图。Shechtman等经进一步研究后断言其内部结构是非周期分布的。他们以“具有长程有序而无平移对称的金属相”为题发表了该项研究。

这个时候，Pennsylvania大学的物理学家Paul Steinhardt与他已毕业的学生Dov Levine正沉迷于Penrose铺砌。在得知Shechtman等的研究结果时，他们意识到这是对他们理论研究最有力的实验支持。两人遂将Penrose拼图及Mackay菱面体三维堆砌中的定点坐标写出来。经傅里叶变换，他们得到5次、3次旋转对称衍射图，并指出Shechtman的结果就是二十面体准晶。该研究以“准晶：一类新的有序结构”为题发表。从此，“准晶”（quasicrystal）一词正式亮相。

1987年，法、日科学家成功地在实验室中应用缓冷技术制得了准晶体。该准晶体达到了几毫米。它足够大到可以做X射线衍射分析。随着高分辨电子显微镜的出现，我们已经可以直观地判断5次对称衍射是来自准晶还是孪晶，于是准晶存在的论断最终被全球同行所公认。

在二十面体这样的三维准晶发现后，人们还陆续发现了大量的二维准晶。这些二维准晶是三维物理空间的材料，原子在其中二维结构上呈准周期分布的，而在另外一维结构上呈周期分布。如今，人们已经发现具有5次、8次、10次和12次等旋转轴的二维准晶。

起初，准晶体获得的条件比较苛刻，如元素要简单、原子半径要相近的金属等。Steinhardt在准晶发现10多年后，突发奇想，他认为准晶存在的合金体系很普通，急冷、缓冷都会有准晶出现，那么以前有人也许错过了对准晶的认定。以往结构的测定主要靠X射线，准晶的谱线未被认识。现在用已知准晶的X射线谱去对比，说不定可以发现些什么。2009年，他们在一距今2亿年的古老岩石中发现了天然准晶化合物，其成分为Al63Cu24Fe13，原来自然界早已存在准晶。

2004年，中国晶体学家郭可信指出二十面体准晶在1980年代被发现有其历史必然性。首先，二十面体密堆理论在1950年代就已成熟，并广泛用于非晶体的结构研究中。其次，电子衍射和高分辨电子显微成像技术在20世纪70年代兴起并在80年代得到普及推广。最后，就是航空航天的发展需要强度更高的铝、镁合金和镍基高温合金。这些需求使科学家们开始采用非传统冶金技术来生产新合金。在此过程中，最先被发现的是急冷凝固形成的Al-Mn准晶。

同当初原子的争论一样，准晶在最初出现时也受到很大的争议。特别是Pauling，他是测定晶体结构起家的，曾发表过很多关于晶体结构的文章，是地地道道的晶体学家。Pauling想方设法要把Shechtman的准晶纳入传统晶体学领域。他辛辛苦苦地写文章捍卫他的正统晶体学观点，还曾认为准晶是胡说。