1.晶面符号

用一些简单的数字来表示不同的晶面，这些数字即晶面符号或晶面指数。晶面符号的种类很多。不过，现代晶体学中通常采用米氏符号。该符号是英国剑桥大学矿物学教授William Hallowes Miller（1801—1880年）于1839年所创，所以也叫米勒指数（Miller index）。晶面符号是用晶面在晶轴上的截距系数的倒数比表示。它有两种表达方式：三轴、四轴。

1）三轴定向

如图2.33所示，设有一晶面HKL，它在x、y、z轴上的截距分别是OH=2a，OK=3b，OL=6c，其中2、3、6为截距系数。截距系数的倒数比为1/2∶1/3∶1/6，化简后为3∶2∶1。去掉比例符号，加圆括号则为（321）。（321）为晶面HKL的晶面符号。通常情况下，我们用（hk l）表示晶面的一般符号。

图2.34为立方晶系的一个晶体。通过晶体中心的三根L4轴分别作x、y、z轴。三根轴交于晶体中心。轴单位为a、b、c。由于该晶体属于立方晶系，故a=b=c。晶面ABCD与y、z轴平行，截距为∞；与x轴相截，截距为轴单位的一半即a/2。据此，晶面ABCD与三根轴的截距系数为1/2、∞、∞。截距系数的倒数为2、0、0。因此，ABCD晶面符号或晶面指数为（200），还可进一步化简为（100）。同理，其他晶面的晶面符号也可得出。

读者在使用晶面符号时需注意以下几个问题。

（1）晶面符号是按照x、y、z轴的顺序排列的。上文的（321）、（100）不能写成（213）、（010）等形式。

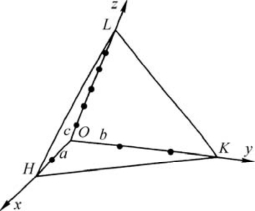
图2.33　晶面符号图解（引自赵珊茸，2004）

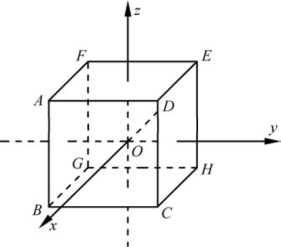
图2.34　晶面符号示例

（2）晶面符号是截距系数的倒数比。因此，晶面在晶轴上的截距系数越大，则在晶面符号中与该轴相对应的数字越小。平行于晶轴，则在该轴上的截距为∞，晶面符号为0，如（301）晶面表示该晶面平行于y轴。

（3）晶面符号可表示出在各晶轴所截轴单位的数目之比。（111）表明晶面与三个晶轴所截轴单位的数目相等。（321）表明晶面所截轴单位的数目不等，分别是1/3、1/2和一个轴单位。

（4）由于晶轴有正、负端，因而晶面符号也要根据晶面截于晶轴正端还是负端来表示。如表示晶面与x轴负端相截。图2.34中，EFGH晶面的晶面符号可表示为

（5）同一晶体中，与晶轴分别相交于坐标原点两端，且截点与原点间的距离分别相等的任何两个互相平行的晶面，它们的晶面符号之绝对值都是相等的，但正、负号彼此相反。如图2.34所示，ABCD、EFGH的晶面符号分别是（100）、（100）。再比如面。

（6）任意一个单形（单形是指各晶面形状相同、大小相等的晶体，如NaCl的立方晶形），不论晶面数是多少，其晶面符号中的数字的绝对值都相等，只是正负号和顺序的变化。图2.34中六个晶面的晶面符号分别是

（7）晶面族。如（6）中所述，在高度对称的晶体中（如立方晶体等单形）存在一些位向不同，但原子排列完全相同的晶面。这些晶面构成晶面族，用｛hkl｝表示。比如：立方晶体的｛100｝晶面族包括（100）、（010）、（001）等晶面；｛111｝晶面族有和等晶面。

（8）晶面符号为（111）的为单位晶面。它在三根晶轴上的截距都是一个轴单位。如图2.34中的FBH面。在中、低晶族中，我们往往要利用单位晶面去比较和确定其他晶面的晶面符号。

2）四轴定向

三轴定向对于六方晶系存在一个缺点：不能显示晶体的六次对称及等同晶面关系。在六方晶系中，晶体学上等价的晶面、晶向用三轴定向表示的晶面符号看起来相差较大，如图2.35（a）中的六方晶系，其六个竖直面实际是等同的，但用三轴定向晶面符号分别是（100）、（010）、。这些符号不如立方晶系的（100）、（010）等那么相似。所以有必要引入第四根晶轴。

四轴定向中，晶面符号的获得与三轴定向一致，也是将截得的轴单位数目取倒数，再化简而得到。不同之处就是多了一根u轴。晶面符号表示为（hkil）顺序依次为x、y、u、z轴。将图2.35（a）中平行于y、z轴的晶面ABCD，往z轴（c方向）负方向投影。经此投影后，晶面ABCD成为图2.35（b）中的AB线。ABCD面与x轴、u轴的截距都是3个轴单位。但交于x轴正方向，交于u轴的负方向。该晶面与x、y、u、z轴的截距分别是：3a、∞、-3u、∞。截距系数的倒数分别是1/3、0、-1/3、0，化简后为1、0、-1、0，故ABCD的晶面符号为。其他晶面符号也可同理得出。

图2.35　（a）六方晶系的晶面符号；（b）六方晶系晶向符号（c轴与纸面垂直，任意两个最近邻交点相距一个轴单位）（引自蔡珣，2010）

四轴定向的晶面符号（hkil）中，前三个指数之和永远是零，即h+k+i=0。它被称为晶面指数总和定理。现证明如下，如图2.36所示，图中虚线表示各轴负方向。

设一晶面与x、y、u轴所在平面的交线为AB（此处不考虑z轴），则该晶面在x、y、u轴上的截距分别是OA=h′a、OB=k′b、OC=i′u，其中a、b、u分别是各晶轴的轴单位。h′、k′、i′分别表示晶面在各轴上的截距系数。图2.36中，过点C作CD∥OB。因为x、y、u轴的正向分别相交成120°，所以△OCD是正三角形，OC=OD=DC，且△ACD∽△ABO。

则OA/OB=AD/DC=（OA-OD）/DC=（OA-OC）/OC，

进一步写成：

两端同时除以h′a：

(www.daowen.com)

移项：

考虑到图2.36中晶面在u轴上的截距为负值，即i′＜0，令i′=-i″，式（2-9）可写成

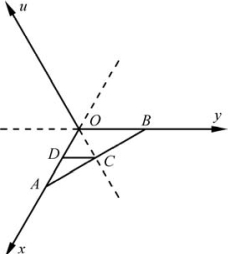
图2.36　晶面指数总和定理证明示意图

如图2.35（b）所示，根据六方晶系的对称性、结点排布特点，我们可知x、y、u轴的轴单位是相等的，即a=b=u。则式（2-10）可化简为

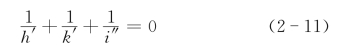
式（2-11）中的每一项恰好是晶面在x、y、u轴上截距系数的倒数，令1/h′=h、1/k′=k、1/i″=i，则有

所以晶面在x、y、u轴上的截距系数的倒数之代数和为0。

有以下几点说明。

（1）在三个水平轴的指数中，如果有一个为0，则其他两个指数大小相等、符号相反。

（2）若三个水平轴指数都不为0，则其中一个指数的绝对值等于另两个指数的绝对值之和，如图2.35（a）中的晶面符号。

（3）由于四轴定向的晶面符号（hkil）中h+k+i=0，故知道其中任意两个指数，其他一个必然也知道了。因此，四轴定向的晶面符号也可写成三轴定向的形式（hkl）。如图2.35（a）中的（0001）可写成（001）；（1120）可写成（110）。

2.晶向符号

与晶面一样，在材料研究中，我们也需要知道晶体中的某些方向。因为不同的方向，有不同的结点间距和面网密度。这些不同会导致材料不同方向的性质有所差异。

由空间解析几何可知，空间中的任何直线方向可用向量表示。只要知道任意两点坐标，就可知道该向量，进而知道向量指示的方向。由于晶体的晶棱也可表示方向，故晶向符号也称为晶棱符号。晶向符号只涉及方向不涉及具体位置，因此任何晶棱或直线都可设想为将其平移通过晶轴的交点O（即坐标系原点），其方向是不变的。

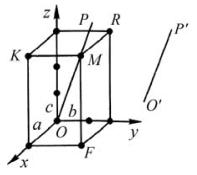
图2.37　晶向符号的表示（引自赵珊茸，2004）

如图2.37所示，晶棱O′P′为晶体的一条晶棱，将其平移至O点成为OP。在OP上任取一点M。向量OM的方向就是晶棱O′P′和OP的方向。O点坐标为（0，0，0），M点的坐标为（a，2b，3c），故只用M点的坐标即可确定晶向符号。同晶面符号一样，取其系数1、2、3后化简，然后加方括号后，即［123］。［123］即晶棱O′P′、OP代表的方向。

对于晶棱符号，应当注意以下几点。

（1）与晶面符号一样，数字的排列顺序为x、y、z轴。三个系数应化为最简单的整数。系数同样有正负之分，如［123］。但此处的系数不用取倒数，这一点与晶面符号不同。

（2）所有平行晶棱的方向是一样的。

（3）同一晶棱的方向指向两端，但代表同一方向。代表两端的晶棱符号，其数字完全反号，如［123］与代表同一晶棱方向。这与数学上的向量不同。

（4）平行于晶轴的晶棱符号即为该晶轴的符号，如平行于x轴的方向为［100］、平行于y轴为［010］、平行于z轴的为［001］。

（5）六方晶系的晶向符号有两种表示方法：一是采用四轴定向，二是采用三轴定向。采用四轴定向常用平移法来确定。如图2.35中的Om方向，从O指向m，起点在O，沿着x轴的正方向移动一个单位（见图2.35中虚线），再沿平行于u轴的方向，向u轴负方向移动一个单位，到达终点m。在此过程中，没有平行于y、z轴的移动，所以在y、z轴上的移动距离为0。取其在每个晶轴上的系数：1、0、-1、0，化简后，写成晶向符号。则就表示Om所指的方向。根据以上介绍的平移法来确定四轴定向的晶向符号，我们还有很多种平移方式都能把起点、终点联系起来，指向同一方向，故同一方向有很多种表示方法。但是这为我们的工作带来了不便。为了与晶面符号的指数总和定理相协调，人们常选取前三个指数之代数和为0的符号表示晶向，如上文的［1010］和图2.35（b）中的其他晶向符号。六方晶系的晶向符号还可采用三轴定向表示，即只用x、y、z轴上的系数比。以上文的为例，见图2.35（b）。过m点作y轴的平行线，与x轴正方向交于n，On=2a；再过m点作x轴平行线，与y轴正方向交于g，Og=b。由于Om在xOy平面，因此没有平行于z轴的移动。故Om在x、y、z轴上的坐标系数分别为2、1、0，化简后写成［210］，所以三轴定向表示的晶向符号［210］与四轴定向表示的晶向符号［1010］是同一方向。实际上，三轴定向与四轴定向表示的晶向符号可相互转化。用［RST］表示三轴定向的晶向符号，［rstw］表示四轴定向的晶向符号。它们的关系可用下式换算：R=r-t；S=s-t；T=w。如［1010］，则r=1，s=0，t=-1，w=0。利用换算关系有：R=1-（-1）=2，S=0-（-1）=1，T=w=0，故三轴定向的晶向符号为［210］。此外，无论是采用四轴定向还是三轴定向，某一晶棱在z轴上的系数都是相同的，故我们在上文的例子中未提到z轴系数。

（6）晶向族。与晶面族类似，等价的晶向构成晶向族，用〈uvw〉表示。等价的晶向具有等价的晶向指数。如立方晶体的〈100〉晶向族包含［100］、［010］、［001］、、和共六个晶向。此外还有〈110〉、〈111〉、〈112〉等晶向族。晶向族中的各晶向数字的绝对值都相等，只是正负号和顺序发生变化。

至此，我们已经知道了面网密度、面网间距及晶面符号、晶向符号的表示方法。这些概念和符号给我们了解晶体的性质带来了很大帮助，比如在受到外力作用时，晶体会在有些晶面上沿着某些方向优先滑动，产生变形。那它们是哪些晶面、哪些方向呢？一般来说，面网间距大，晶面之间的作用力较弱，容易分开。所以面心立方（fcc）、体心立方（bcc）等晶体结构的晶体，其面网密度大的晶面总是容易沿着最密集的方向滑动。原子在最密集的方向上滑动很短的距离就能达到先前的受力平衡状态。图2.26中的Cu属于面心立方晶体结构。Cu的（111）面是密排面，故Cu容易沿着最密排的［110］方向滑动变形。当然，晶体的滑动变形还与温度、成分等有关，这里不做讨论。滑移面和滑移方向组成滑移系统。滑移系统越多，晶体材料越容易发生变形而不开裂。金属材料的滑移系统往往比无机非金属材料的滑移系统多。这是金属往往比无机非金属材料容易变形的原因之一。

晶面与相关的晶向是否能用一个数学关系统一起来呢？其实，2.4.4节介绍的晶带定律就总结出了这个规律。下面对此做一推导。