综合考虑单位平行六面体的七种形状和四种结点分布类型，七种晶系应有7×4=28种不同形式的格子。这28种格子中有些不符合单位平行六面体的对称特点；有些不符合平行六面体的选择原则；有些还可以改换划分方式。最终只剩下14种形式的格子，称为布拉维格子（bravais lattices），其中的阵列也叫布拉维点阵，见附录2。布拉维格子是空间格子的基本组成单位。只要知道了格子的结点分布情况，以及a、b、c和α、β、γ等参数后，就可以知道整个空间格子的一切特征。

需再次强调，空间格子或布拉维格子中的点是晶体结构的几何学抽象。布拉维格子代表晶体中原子分布规律的结点之集合，其中每个结点周围的环境是相同的。这与晶体结构中质点（如原子、离子等）的排列方式是无限的有所不同。通常说某某结构时常常指的是晶体结构，而说某某点阵时常常指的是空间格子的点阵类型。晶体结构与点阵既有联系又有区别。点阵是晶体结构抽象出来的。在某些情况下，点阵中的结点位置可以是晶体结构原子的位置。这时晶体结构与点阵没有差别，一些简单金属，如图2.26中的Cu是面心立方点阵，也是面心立方结构（常用fcc表示）。图2.27中的Cr是体心立方点阵，也是体心立方结构（常用bcc表示）。但在大多数情况下，晶体结构是不同于点阵的。晶体结构与点阵的关系可表示为：点阵+基元=晶体结构。

图2.26　具有相同点阵的晶体结构（引自蔡珣，2010）(www.daowen.com)

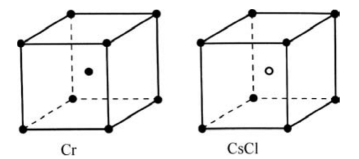
图2.27　晶体结构相同而点阵不同

基元是指数种原子构成的基本结构单元。比如NaCl晶体，一个Na-Cl原子或离子对可构成基元。把一个个的基元重新按规律放回点阵中的结点位置就是晶体结构。可见，这是把晶体结构抽象成点阵的逆过程。

图2.26表示了Cu、NaCl、CaF2三种晶体结构。这三种结构有很大差异，属于后文要介绍的不同晶体结构类型。但是，它们都属于面心立方格子或点阵。图2.27中的Cr、CsCl的晶体结构都是体心立方结构，但Cr属于体心立方格子，CsCl属于立方原始格子或简单立方格子。