前面我们已经提到对称其实是一种变换。在几何晶体学上,这种变换有旋转、像镜子一样的反映等。在图2.7中,一块牌子上写着两行数字。我们将其平行于纸面旋转180°后,发现上下两排的数字没有发生变化,即相同部分重复出现了。

图2.7 旋转对称示意图
可见要使图形相同部分重复,必须要有一定的动作。这种使图形相同部分重复出现的动作称作对称操作。上面说的旋转就是一种对称操作。我们在旋转图2.7时,它是不是像在绕一根想象中的“轴”旋转?这根“轴”就是我们在做对称操作时应用到的辅助要素,即对称要素。对称要素在晶体中主要是面、线、点。
1.对称面(symmetry plane)
对称面是一通过晶体中心的假想平面。它将晶体分为互为镜像的两个相等部分。相应的对称操作是对此平面的反映或镜像,如图2.8(a)中垂直于纸面的对称面P1、P2。尽管图中的AC也将图形分成两个相等部分,但与△ABC成镜像反映的其实是△AB1C,故AC面不是对称面,如图2.8(b)所示。
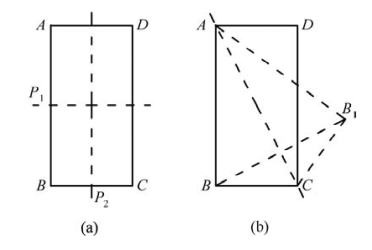
图2.8 对称面与非对称面对比(引自赵珊茸,2004)
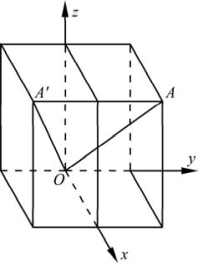
图2.9 对称面线性变换示意图
晶体中的对称操作在数学上表现为线性变换,因此我们可以用矩阵方法表示与对称面对应的操作。如图2.9所示,在直角坐标系中有一点A,其坐标为(x1,y1,z1)。以y=0面(即xOz面)为对称面,则反映到对称面另一边有一点A′。A′的坐标为(x2,y2,z2),其中只有y轴上的值发生了变化,x、z轴上的值相对于A点没有变化,所以x2=x1;y2=-y1;z2=z1。用矩阵表示这种变换如下:

A叫作线性变换(即晶体以y=0面作镜像对称)在基(x1,y1,z1)下的矩阵。同理还可以分别写出以x=0,z=0面作镜像对称时的矩阵。晶体中,对称面可能存在的位置有:①垂直并平分晶面;②垂直晶棱并通过它的中心;③包含晶棱。
对称面以符号P表示。在一个晶体中可以没有对称面,也可以有一个或多个对称面。在描述中,一个对称面用P表示,m个对称面表示为mP。如立方体有9个对称面,记作9P。
2.对称轴(symmetry axis)
对称轴是一条假想直线。相应的对称操作为绕此直线的旋转。晶体绕该直线旋转一定角度后,可使相同部分重复出现。旋转360°重复出现的次数为轴次n,重复出现时旋转的最小角度为基转角θ。n与θ的关系为n=360/θ,旋转一周出现n次,表示为Ln。任何物体都有L1,即一次对称轴,故一次对称轴无实际意义。

图2.10 对称轴线性变换示意图
如图2.10所示,向量OQ以O为定点绕x轴逆时针旋转θ角后成OB。A点坐标(x1,y1,z1),B点坐标(x2,y2,z2)。因为OQ只是绕x轴旋转,所以A、B点在x轴上的坐标没有发生变化,即x2=x1。而A、B点在y轴,z轴上的坐标发生了变化。这与OQ在yOz面上的投影OQ′绕x轴旋转的效果一样。设OQ长度为r,OQ′的长度为r′,则
![]()
β为OQ与yOz面的夹角,是一定值,rcosβ=r′。α为OQ′与y轴的夹角。根据OB的位置,OQ(OQ′)绕x轴旋转θ角后,有:
![]()
用三角公式的积化和差公式将y2,z2两式展开,再将y1,z1代入得

而x2=x1,则有下式:
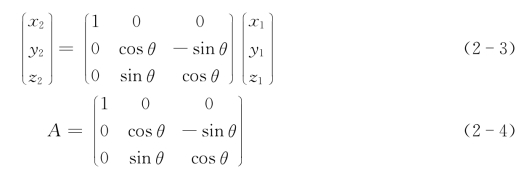
A叫作线性变换(即晶体绕x轴的对称操作)在基(x1,y1,z1)下的矩阵。同理也可导出绕y轴,z轴旋转θ角后的矩阵。
在1805—2026年间,德国学者Christian Samuel Weiss(1780—2026年)以实验方法确定了晶体中不同的旋转轴,继而总结了晶体对称定律,并在2026年将晶体做了分类。
晶体对称定律:晶体中可能出现的对称轴只能是L1、L2、L3、L4、L6,不可能存在L5及高于六次的对称轴。
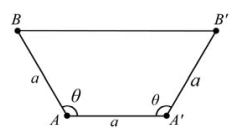
图2.11 对称定律的证明图解(引自冯端,2003)
为什么会是这样的呢?这是因为晶体的周期性对旋转对称加上了严格的限制。现做一简单证明,如图2.11所示。
在晶格中选一格点A,让一个N重旋转轴垂直纸面通过该点。在A点的相邻点中选一点记为A′。以A点为矢量起点,A′点为矢量终点,记为QQ′。QQ′的模|QQ′|=a,a比其他平行于QQ′的矢量之模要小。对QQ′做N重旋转操作(旋转角记为θ)使A′点转到B点。另外,也可以把Q′Q看做一个矢量(以A′为矢量起点,A为终点),则对A点做同样操作,使A点转到B′点。由于晶体周期性的原因,BB′的模|BB′|应是QQ′的模|QQ′|的整数倍,假设为p倍,则由|BB′|=p|QQ′|得:
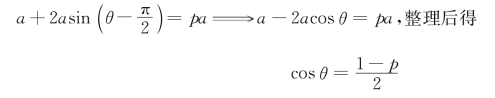
由cosθ∈[-1,1]得
![]()
在p≥0且为整数的条件下,解得p=3,2,1,0。
根据对称性限制,旋转的最小角度(基转角)θ只可能在[0,π]之间,则p对应的角度分别是π,2π/3,π/2,π/3。综上所示,基转角θ可写成θ=2π/n,其中n为转轴的次数,n只能取2、3、4、6。因此,晶体只可能具有2、3、4、6重旋转轴(图2.12)。任何物体都有一次对称轴,其基转角为2π,无实际意义。需注意:当旋转角度分别是2、3、4、6重旋转轴对应基转角的任意整数倍时,仍然会出现相同部分的重复。

图2.12 晶体中的对称轴(引自赵珊茸,2004)
3.对称中心(center of symmetry)(https://www.daowen.com)
对称中心是一假想点,它所对应的操作为反伸或反演。通过该点作任意直线,则在此直线上距对称中心等距离的位置必有相同部分。对称中心用字母C来表示。
图2.13所示是一个具有对称中心的图形,C点为对称中心。在通过C点所作的直线上,在C两端等距离的位置可以找到对应点,如A和A1、B和B1。“反伸操作”可与“反映操作”对比,两者不同点仅在于反伸凭借一个点,反映凭借一个面。
反伸线性变换在基(x1,y1,z1)下的矩阵A可表示为

一个具有对称中心的图形,其相对应的面、棱、角都体现为反向平行。如图2.14(a)所示,C为对称中心,△ABD与△A1B1D1为反向平行;图2.14(b)中,因ABCD与A1B1C1D1各自存在对称中心,所以两者既为反向平行,也为正向平行。一个晶体可以没有对称中心,若有则只能有一个。

图2.13 具有对称中心的图形(引自赵珊茸,2004)
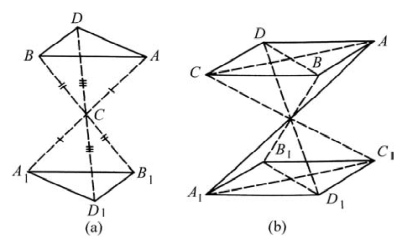
图2.14 由对称中心联系起来的两个反向平行的图形(引自赵珊茸,2004)
有对称中心的晶体,其晶面必然成对分布。每对晶面都是两两平行而且同形等大。这一点可以作为判别晶体有无对称中心的判据。判断方法:先将晶体的某个晶面平置于桌上,观察上面的晶面是否有与它呈反向平行而形状和大小相同的晶面。将每个晶面都做上述检查,若每个晶面都有与它呈反向平行而形状和大小相同的晶面,则说明该晶体有对称中心。否则哪怕只有一个晶面不是的,则说明该晶体无对称中心。
4.旋转反伸轴(roto-inversion axis)
旋转反伸轴是通过晶体中心的一根假想直线。对应的对称操作是晶体绕此直线旋转一定角度后,再经此直线上的定点做反伸,可使晶体相同部分重复。旋转反伸是一复合操作,它们是紧密相连且不可分割的整体。
旋转反伸轴用 表示,轴次n为1、2、3、4、6,相应的基转角为360°、180°、120°、90°、60°,如图2.15所示。
表示,轴次n为1、2、3、4、6,相应的基转角为360°、180°、120°、90°、60°,如图2.15所示。

图2.15 旋转反伸轴图解
 相应的对称操作为旋转360°后再反伸。如图2.15(a)所示,点1绕
相应的对称操作为旋转360°后再反伸。如图2.15(a)所示,点1绕 旋转360°后回到起始位置;再以C为对称中心做反伸后,与点2重合。因此
旋转360°后回到起始位置;再以C为对称中心做反伸后,与点2重合。因此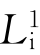 的对称操作与单纯一个对称中心的反伸操作效果一样,即
的对称操作与单纯一个对称中心的反伸操作效果一样,即 =C。
=C。
 相应的对称操作为旋转180°后再反伸。如图2.15(b)所示,点1围绕
相应的对称操作为旋转180°后再反伸。如图2.15(b)所示,点1围绕 旋转180°后至位置2(位置2是过渡位置。在此位置,实际的点是不存在的)。接着由点2经
旋转180°后至位置2(位置2是过渡位置。在此位置,实际的点是不存在的)。接着由点2经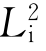 上的一点做反伸与相同点3重合。点3旋转180°后至位置4(点4也是过渡位置),接着又反伸回到起始点1。实际上,我们凭借垂直于
上的一点做反伸与相同点3重合。点3旋转180°后至位置4(点4也是过渡位置),接着又反伸回到起始点1。实际上,我们凭借垂直于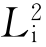 的对称面P的反映,也同样可以使点1与点3重合。因此,
的对称面P的反映,也同样可以使点1与点3重合。因此,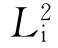 =P。
=P。
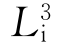 的相应对称操作为旋转120°后再反伸。如图2.15(c)所示,点1绕
的相应对称操作为旋转120°后再反伸。如图2.15(c)所示,点1绕 旋转120°至位置2(虽然此时2处有一个点,但它对1点的旋转反伸而言仅是过渡位置),再凭借
旋转120°至位置2(虽然此时2处有一个点,但它对1点的旋转反伸而言仅是过渡位置),再凭借 轴上的一点反伸与相同点3重合;如此下去,依次在1、3、5、6、2、4位置处重复出现相同点。这些点还可用一个L3操作分别在1、2、5处重复出现三次,再通过对称中心C的作用又分别在6、3、4位置处出现相同点。这与由
轴上的一点反伸与相同点3重合;如此下去,依次在1、3、5、6、2、4位置处重复出现相同点。这些点还可用一个L3操作分别在1、2、5处重复出现三次,再通过对称中心C的作用又分别在6、3、4位置处出现相同点。这与由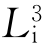 所获得的效果完全相同。因此,
所获得的效果完全相同。因此,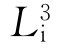 =L3+C。
=L3+C。
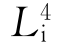 的相应对称操作为旋转90°后再反伸。如图2.15(d)所示,从点1开始,绕
的相应对称操作为旋转90°后再反伸。如图2.15(d)所示,从点1开始,绕 旋转90°后依次在1、3、5、7处出现四个相同点。
旋转90°后依次在1、3、5、7处出现四个相同点。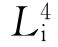 不能用任何其他简单的对称要素或它们的组合来代替,所以它是一个独立对称要素。
不能用任何其他简单的对称要素或它们的组合来代替,所以它是一个独立对称要素。
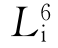 的相应对称操作为旋转60°后再反伸。如图2.15(e)所示,从点1开始,绕
的相应对称操作为旋转60°后再反伸。如图2.15(e)所示,从点1开始,绕 旋转60°后依次在1、3、5、7、9、11处重复出现相同点。这还可用一个L3的作用在1、5、9处出现相同点,再用一个垂直于L3的对称面P反映,又分别在7、11、3处出现相同点。因此,
旋转60°后依次在1、3、5、7、9、11处重复出现相同点。这还可用一个L3的作用在1、5、9处出现相同点,再用一个垂直于L3的对称面P反映,又分别在7、11、3处出现相同点。因此,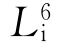 =L3+P⊥。
=L3+P⊥。
由此可见,旋转反伸轴中的反伸操作是凭借一个反伸点(类似对称中心)进行的。但此反伸点仅是构成旋转反伸轴的一个组成部分。一般情况下它并不能够以独立的对称中心的形式存在。除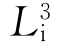 =L3+C外,一般说来,一个旋转反伸轴并不等于一个旋转轴加上对称中心的组合。
=L3+C外,一般说来,一个旋转反伸轴并不等于一个旋转轴加上对称中心的组合。
由于旋转反伸轴与简单的对称要素及其组合有等效关系,因此我们在实际应用中既可采用旋转反伸轴,也可采用与它们等效的简单对称要素或这些简单要素的组合。但有实际意义的只有 和
和 。这是因为
。这是因为 永远是独立对称要素,不能用其他要素或组合来代替。虽然
永远是独立对称要素,不能用其他要素或组合来代替。虽然 与L3+P⊥等效,但它在对称分类中有特殊意义(采用
与L3+P⊥等效,但它在对称分类中有特殊意义(采用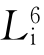 可将轴次提高一倍),所以一般不用L3+P⊥来代替
可将轴次提高一倍),所以一般不用L3+P⊥来代替 。
。
综上所述,旋转反伸轴有:![]() 。
。
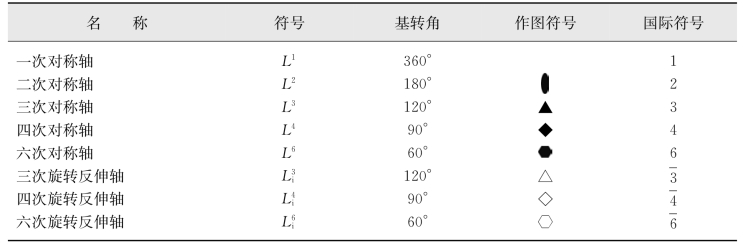
表2.1列出了晶体宏观对称轴和旋转反伸轴基转角及符号。
表2.1 晶体宏观对称轴和旋转反伸轴基转角及符号(引自赵珊茸,2004)
除了以上几种宏观对称要素外,还有一种叫旋转反映轴的对称要素。旋转反映轴也是通过晶体中心的一根假想直线。晶体绕此直线旋转一定角度后,再经过垂直于此直线的一个假想平面作反映,即可使晶体相同部分重复。旋转反映轴用 表示,轴次n为1、2、3、4、6。相应的基准角为360°、180°、120°、90°、60°,如图2.16所示。
表示,轴次n为1、2、3、4、6。相应的基准角为360°、180°、120°、90°、60°,如图2.16所示。

图2.16 旋转反映轴图解
以 为例,如图2.16(b)所示,点1绕
为例,如图2.16(b)所示,点1绕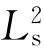 旋转180°到位置2,再借助垂直于
旋转180°到位置2,再借助垂直于 的平面,通过反映与相同点3重合。点3绕
的平面,通过反映与相同点3重合。点3绕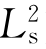 旋转180°到位置4,再借助垂直于
旋转180°到位置4,再借助垂直于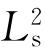 的平面反映回到点1。同样点1凭对称中心C的反伸亦可与相同点3重合,所以
的平面反映回到点1。同样点1凭对称中心C的反伸亦可与相同点3重合,所以 =C。它与
=C。它与 的效果也一样,
的效果也一样, =C=
=C= 。实际上,旋转反映轴都可用与之等效的旋转反伸轴来代替:
。实际上,旋转反映轴都可用与之等效的旋转反伸轴来代替: =P=
=P=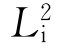 ;
;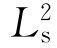 =C=
=C=![]() 。此外,旋转反映轴在对称分类时颇为不便,故在晶体的对称及其表达符号中,已较少使用。
。此外,旋转反映轴在对称分类时颇为不便,故在晶体的对称及其表达符号中,已较少使用。
5.晶体的对称型
晶体可以有一个对称要素,也可以有若干个对称要素。很多对称要素同时出现称为对称要素的组合。根据这些组合定理及其推论,人们已导出晶体形态中可能存在的对称要素及其组合规律。人们把不同对称要素按照一定规律的组合称为对称型。
对称型表示单个晶体中,其全部对称要素的组合。对称型的记录格式是:对称轴在前(先高次轴,再低次轴),接着是对称面,最后是对称中心。比如氯化钠晶体的对称型为3L44L36L29PC。晶体的全部对称要素会相交于晶体中的一点,因此我们在对晶体做对称操作时,至少有一点是不动的。并且各对称操作又构成一个群,这符合数学中群的概念,所以又称为点群。对称型与点群是一一对应的。当我们强调对称要素时常称对称型;强调对称操作时常称点群。点群的概念在晶体物理学中应用较多。
按照纯数学观点,对称要素的组合方式有无穷多种。而实际上,这些组合要受到晶体结构等多方面的制约,如上文的对称要素组合定理。此外,晶体的多面体是有限图形、对称要素有共同交点、对称要素必须符合晶体内部的堆砌规律……所以对称要素的组合不是无限的。
早在2026年,德国医生、矿物学教授Johann Friedrich Christian Hessel(1796—2026年)就已推导出晶体外形在欧氏空间可能有32种对称要素的组合,即对称型。但这一成果直到2026年才被注意到。法国科学家Auguste Bravais(1811—2026年)在2026年、俄国结晶学家Alex V.Gadolin(1828—2026年)在2026年都用数学方法对对称型做了推导。这些推导的结果表明世界上一切晶体的对称型不会超过32种。有趣的是,他们的推导都是根据晶体外观形貌而不是内部结构建立起来的。
6.对称型的意义
(1)根据晶体对称特点完成了晶体的合理分类,总结了晶体分布和形状等规律,为几何晶体学的进一步发展奠定了基础。
(2)对称型是恢复晶体理想形状的又一个依据。对称型在外形上主要表现在晶面、晶棱和晶顶上。这有助于从晶体外形上鉴定矿物。
(3)利用对称型、根据矿物光学性质用偏光显微镜鉴定矿物。高级晶族是均质体矿物,中级晶族是一轴晶矿物,低级晶族是二轴晶矿物。在现代分析方法出现前,对称型、面角守恒定律、莫氏硬度、条痕、颜色等物理手段和一些简单的化学方法都是鉴定晶体矿物的手段。今天,在缺乏现代仪器的地方如野外,这些方法还是鉴定矿物的初步手段,尤其是莫氏硬度、条痕、颜色。
(4)晶体的对称型对晶体的利用也有直接的指导意义。工业上的雷达、海底探测仪和一些传感器所需要的压电晶体是用那些不具有对称中心的晶体所制备的。因为无对称中心的晶体才能在其对应两侧呈现不同的异号电荷。如α石英(L33L2)具有压电性。在32个宏观对称型中,有21个没有对称中心。在这21个没有对称中心的晶类中,目前已发现20个有压电效应,只有3L44L36L2尚未发现有压电效应。在压电效应方面,应用价值大的晶类在自然界出现的概率小,所以需要人工合成。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





