1.网架节点设计与构造

（1）焊接空心球节点 它是把两块圆钢板经热压或冷压成两个半球后对焊而成，如图7-91所示。其构造简单，受力明确，并且连接方便，适用于钢管杆件的各种网架。只要将圆钢管与本身轴线切割垂直，杆件与空心球自然对中而不产生节点偏心。由于球体无方向性，可与任意方向的杆件连接。焊接空心球节点分加肋和不加肋两种。

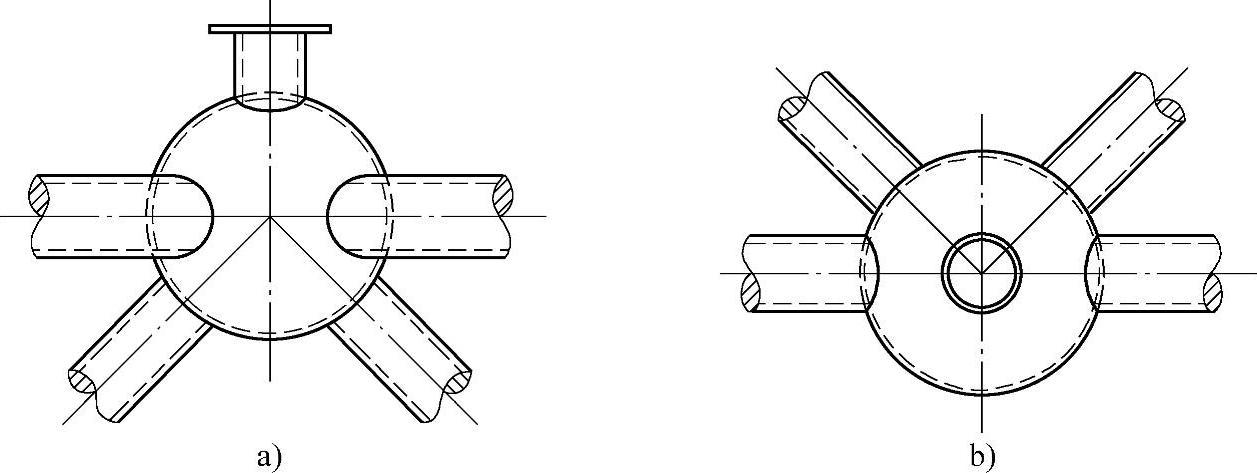
图7-91 焊接空心球节点

a）上弦节点 b）下弦节点

球体直径通常先由构造决定，然后通过计算确定壁厚。球面上相连杆件间的间隙a不宜小于10mm，如图7-92所示。为了确保间隙a，空心球直径可按照式（7-94）估算。

式中 θ——汇交于球节点任意两钢管杆件间的夹角（rad）；

d₁、d₂——组成θ角的两钢管外径。

在一个网架中，节点的种类通常不宜超过3～5种。

空心球壁厚通常为其外径的1/25～1/45；空心球壁厚同相连钢管最大壁厚之间的比值宜为1.2～2.0；空心球壁厚一般不小于4mm。

当空心球外径大于或等于300mm，并且杆件内力较大需提高其承载力时，可在球内两半球对焊处增设肋板，使肋板与两半球焊成一体，如图7-93所示。肋板厚度不应小于球体壁厚，肋板通常可挖空球体直径的1/2～1/3，以减轻自重。为便于两半球的拼装，肋板可用凸台，凸台的高度不得大于1mm。内力较大的杆件应位于肋板平面之内。加肋板后球体的承载力可提高10%～40%。

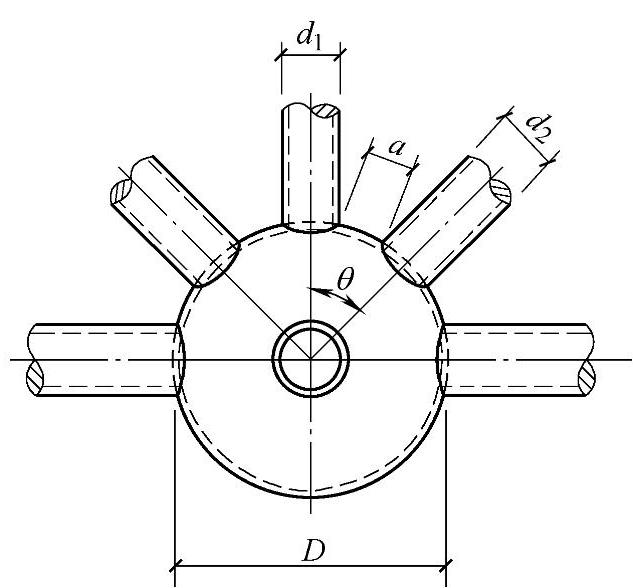
图7-92 焊接空心球构造要求

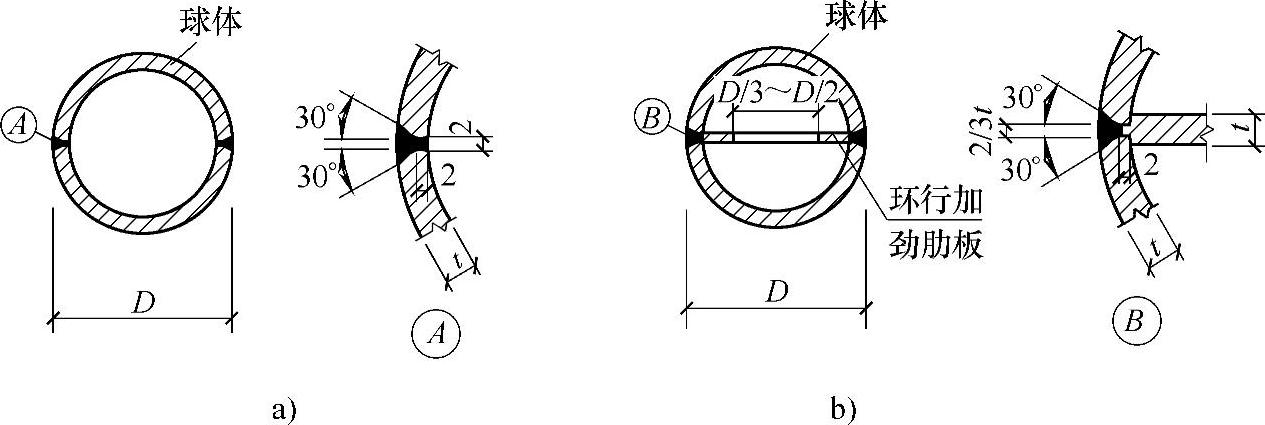
图7-93 焊接空心球肋板的设置

a）无肋空心球 b）加肋空心球

当空心球直径为120～500mm时，其受压、受拉承载力设计值可分别按照式（7-95）、式（7-96）计算。

1）受压空心球：

式中 N_c——空心球的轴向压力设计值（N）；

D——空心球外径（mm）；

t——空心球壁厚（mm）；

d——钢管外径（mm）；

η_c——受压空心球加劲肋承载力提高系数，不加劲为1.0，加劲为1.4。

2）受拉空心球

N_t≤0.55η_ttdπf（ 7-96）

式中 N_t——空心球的轴向拉力设计值（N）；

t——空心球壁厚（mm）；

d——钢管外径（mm）；

f——钢材强度设计值（N/mm²）；

η_t——受拉空心球加劲肋承载力提高系数，不加劲为1.0，加劲为1.1。

钢管同空心球节点焊接时，钢管应开坡口，并在钢管与空心球之间留一定间隙以确保焊透，从而实现焊缝与钢管等强，否则应按角焊缝计算。为保证焊缝的质量，钢管端头可加套管与空心球焊接，如图7-94所示。

对于小跨度的轻屋面网架，钢管与空心球的连接可采用角焊缝，角焊缝的焊脚尺寸h_f应满足以下要求：

①当t≤4mm，h_f≤1.5t，且不宜小于4mm；

②当t＞4mm，h_f≤1.2t，且不宜小于6mm。

其中t为与空心球相连的钢管壁厚。

焊接空心球的钢材宜采用国家标准《碳素结构钢》（GB/T700—2006）所规定的Q235钢或国家标准《低合金结构钢技术条件》（GB/T1591—2008）所规定的Q345钢。

（2）螺栓球节点 由球体、高强螺栓、销子（或螺钉）、六角形套筒以及锥头或封板组成。球体是锻压或铸造的实心钢球，在钢球上根据网架杆件汇交的角度钻孔并车出螺扣。为减小球的体积，在杆件两端各焊一个锥头，放入螺栓，在它的外端套上两侧开有长槽的六角形套筒。拼装时，先把杆件端部的螺栓拧入螺栓球节点的螺纹孔中，然后在套筒长槽部位插入销子，拧转套筒时利用销子带动螺栓转动，使螺栓旋入球体，直至紧固为止，如图7-95所示。

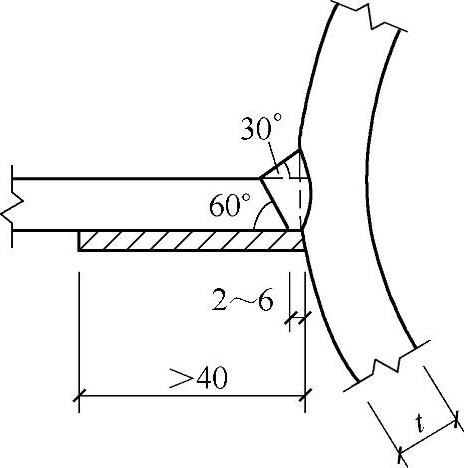
图7-94 焊接空心球加套管焊接

图7-95 螺栓球节点

螺栓球节点除具有焊接空心球节点对空间汇交的钢管杆件连接适用性强及杆件连接不会严生偏心的优点外，还避免了现场焊接作业，并具有运输与安装方便的特点。螺栓球节点通常适用于中、小跨度的网架，杆件最大拉力以不超过700kN，杆件长度不宜超过3m。

1）螺栓球。螺栓球直径同螺栓的直径及螺栓伸入球体内的长度相关，同时还要确保相邻两根螺栓伸入球体内不能相碰。依据几何关系，由图7-96，螺栓球的直径D为

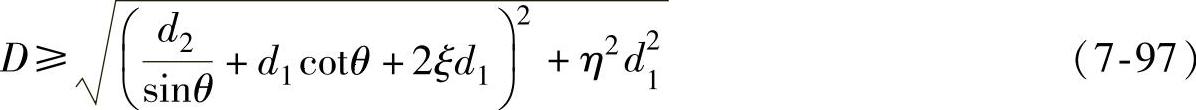
同时应满足套筒接触面的要求，尚应按式（7-98）核算。

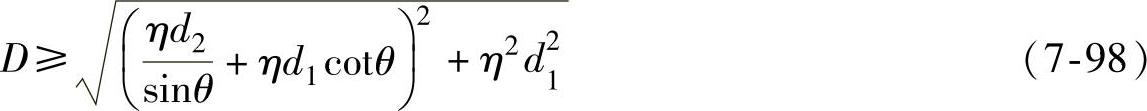
式中 D——球体直径（mm），取两式计算的较大值；

d₁、d₂——螺栓直径（mm），d₁＞d₂；

θ——两个螺栓之间的最小夹角（rad）；

ξ——螺栓伸入球体的长度与螺栓直径的比值；

η——套筒外接圆直径与螺栓直径的比值。

ξ和η值应分别依据螺栓承受的拉力和压力设计值确定，其值可取ξ=1.1，η=1.8。

2）高强度螺栓。依据国家标准《钢网架螺栓球节点用高强度螺栓》（GB/ T16939—1997），螺栓性能等级及推荐材料见表7-14；螺栓材料试件的机械性能应符合表7-15的规定；常用螺栓的拉力载荷试验值应符合表7-16中的规定。

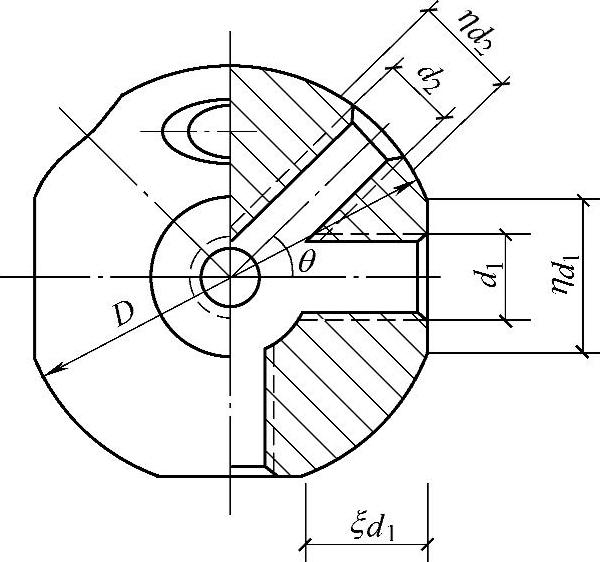
图7-96 螺栓球节点尺寸

表7-14 螺栓性能等级及推荐材料

表7-15 螺栓材料试件机械性能

表7-16 螺栓拉力载荷试验值

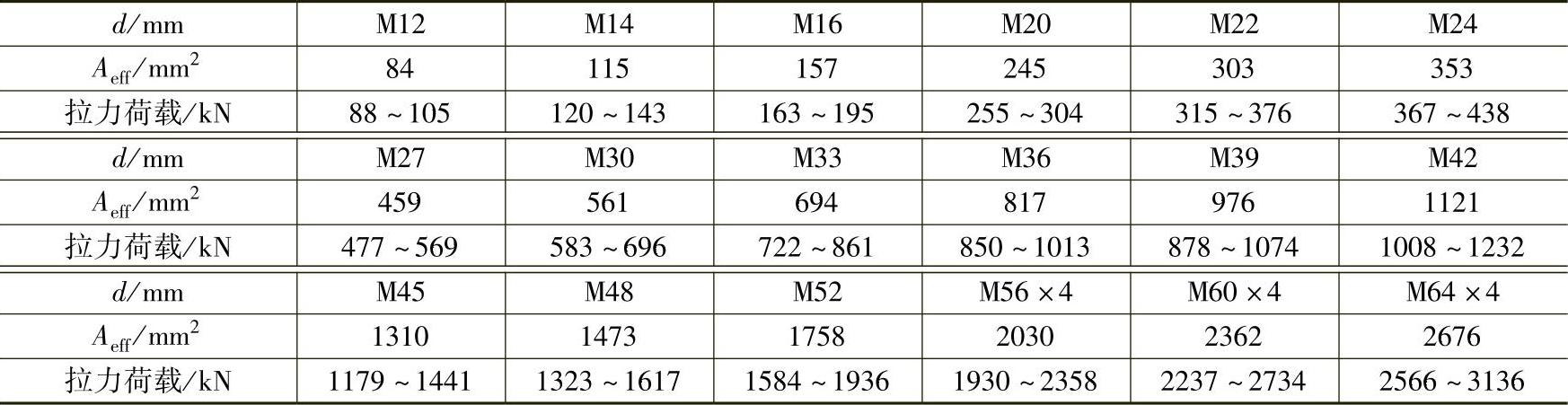
每个高强度螺栓的受拉承载力设计值计算式为

N^b_t≤ψA_efff^b_t （7-99）

式中 N^b_t——高强度螺栓的拉力设计值（N）；

ψ——螺栓直径对承载力影响系数，当螺栓直径小于30mm时，ψ=1.0；当螺栓直径大于等于30mm时，ψ=0.93；

A_eff——高强度螺栓的有效截面面积（mm²），可按表7-16选取，当螺栓上钻有销孔或键槽时，应取螺纹处或销孔键槽处二者中的较小值；

f^b_t——高强度螺栓经热处理后的抗拉强度设计值；对40Cr、40B钢与20MnTiB钢，取430N/mm²，对45号钢，取365N/mm²。

3）套筒。套筒的作用是拧紧高强度螺栓和承受钢管杆件传来的压力，所以套筒的壁厚应根据被连接杆件的轴心压力通过计算确定，并应验算开槽处和端部有效截面的承载力。

套管的外形尺寸应符合扳手开口尺寸系列，要保持端部平整，内孔径一般比螺栓直径大1mm。套筒端部到开槽端部之间的距离应使该处有效截面抗剪力不低于销子（或螺钉）抗剪力，并且不应小于1.5倍的开槽宽度。

套筒长度（mm）可按照式（7-100）、式（7-101）进行计算（图7-95）。

l=a+2a₁ （7-100）

a=ξd₀-a₂+d_s+4mm （7-101）(www.daowen.com)

式中 d_s——销子直径（mm）；

a₁——套筒端部到滑槽端部的距离（mm）；

ξd₀——螺栓伸入球体的长度（mm）；

a₂——螺栓露出套筒的长度，可预留4～5mm，但不少于2个螺扣。

4）封板、锥头。杆件可采用封板或锥头连接，如图7-97所示，其连接焊缝以及锥头的任何截面应同连接的钢管等强；连接焊缝应采用完全焊透的坡口对接焊缝，其中焊缝宽度b可根据连接钢管壁厚取2～5mm。

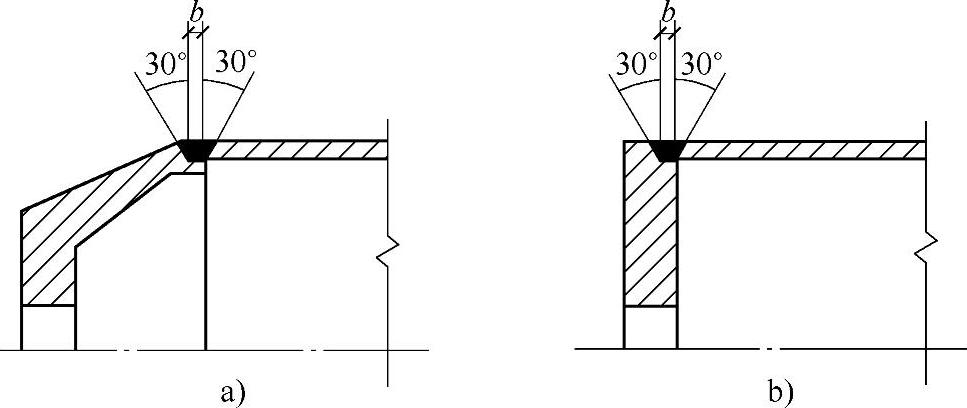
图7-97 杆件端部连接焊缝

a）锥头与钢管连接 b）封板与钢管连接

为防止汇交于节点的杆件相互干扰并使其传力顺畅，当管径大于或等于76mm时，通常宜采用锥头的连接形式；当管径小于76mm时，可采用封板。封板与锥头底板的厚度t_p可依据实际受力大小按塑性理论按照式（7-102）计算。

式中 N——钢管所受拉力设计值（N）；

r——封板或锥头底板的半径（mm）；

s——自封板或锥头底板中心到螺母外边缘的距离（mm）；

f——钢材的强度设计值（N/mm²）。

同时当钢管壁厚小于4mm时，不宜使封板厚度小于钢管外径的1/5。锥头的底板厚度不宜小于钢管外径的1/6。

5）销子或螺钉。销子通常采用高强冷拔钢丝制造，其直径一般可取高强度螺栓直径的0.16～0.18倍，并且不宜小于3mm，也不宜大于8mm。

紧固螺钉通常采用高强度钢材制造，其直径一般可取高强度螺栓直径的0.2～0.3倍，并且不宜小于4mm，也不宜大于10mm。

2.网架节点计算

平板网架是由很多杆件根据一定规律组成的空间桁架体系，属于高次超静定结构。要精确地分析它的内力及变形相当复杂，工作量很大，一般都进行一些假设和简化。按照计算结果的精确程度可分为精确法与近似法两种。常用的精确计算方法有空间桁架位移法；而常用的近似计算方法则有交叉梁系分析法、拟板法以及假想弯矩法等。

（1）计算假定

1）网架结构的节点忽略刚度影响，假设节点为铰接，连接圆球铰的杆件可以绕经过铰中心的任意轴线转动。

2）网架结构上作用的荷载根据静力等效原则，把节点所辖区域内的荷载汇集到该节点上为节点荷载，所以杆件只受轴向力。但当杆件上作用有局部荷载时，则应将局部弯矩的影响另外考虑，此时杆件为拉弯或压弯构件。

3）网架结构的内力和位移计算可按照弹性阶段进行。

（2）空间桁架位移法 又称矩阵位移法。

1）基本假定。

①网架节点皆为理想铰接点。

②结构材料处于弹性工作阶段。

③在荷载作用下，网架为小变形。

2）计算方法。

①以网架结构的各杆件作为基本单元，以节点三个线位移作为基本的未知量，先分析杆件单元，根据虎克定律建立单元杆件的内力及位移间的关系，形成单元刚度矩阵，并列出网架中每一杆件的单元刚度矩阵。

②依据各节点的变形协调条件及静力平衡条件建立结构各节点荷载与节点位移间的关系，形成结构的总刚度矩阵与总刚度方程。

③结构总刚度方程组是一组以节点位移作为未知量的线性代数方程组，引入给定的边界条件，并利用计算机计算出各节点的位移值。

④由单元杆件的内力和位移间的关系，求出杆件内力N值。

⑤杆件的承载力计算。

求得N值后，即可按照轴心受力构件进行强度、刚度和稳定验算。对拉杆按N/A_n≤f进行验算；对压杆按N/（φA_n）≤f进行验算。

3）适用范围。空间桁架位移法是一种精确计算方法，计算结果接近于结构实际受力状况，具有较高的计算精度。它可以被用于计算各种类型、各种平面形状、不同边界条件以及不同支承方式的网架，还能考虑网架与下部支承结构间的共同工作。对由于地震作用、温度变化以及支座升降等因素所引起的内力和变形也可依据工程需要进行内力和变形计算。

空间桁架位移法解网架结构内力及位移的商业软件有多种，可供设计时选用。

（3）简化计算方法 平板网架的节点有很多，若采用空间桁架位移法计算时，则工作量很大，因此为了简化计算，可采用一些近似计算方法。适用于交叉桁架系网架的有交叉梁系差分法与交叉梁系梁元法等；适用于四角锥与棋盘形网架的有假想弯矩法；还有适用范围较广的拟板法与拟夹层板法等。

1）交叉梁系梁元法。该方法的基本思路是：将空间桁架简化为交叉梁系，并在节点处分开成为若干个离散的单元梁，以节点位移作为未知数，用矩阵位移法来求解，从而得到杆件内力。在建立单元梁的刚度矩阵时，将中面变形的影响忽略，只考虑竖向位移及转角。实际工程中，常用差分法用求解代数方程式的方法进行计算。该法同精确法相比，计算误差为10%～20%，目前，对于跨度不大（L≤40m），网格数不多的交叉梁系网架和正放四角锥网架，可以采用此法进行计算，并有计算图表可直接查用。

2）拟板法，也叫拟夹层板法。它是将网架简化为各向同性或各向异性的平板，根据弹性平板弯曲理论建立偏微分方程，用差分法或级数法解出挠度、弯矩和剪力，然后再求出杆件内力。

该法适用于跨度L≤40m的平面桁架或角锥体组成的网架。通常可按图表计算，其计算误差不大于10%。

3）假想弯矩法。该方法是假设网架节点皆为铰接，并在网架的下弦节点上加一个假想弯矩，即未知弯矩，使之能符合平衡要求；根据静力平衡条件导出弯矩方程；然后，再逐个节点将以假想弯矩为未知数的多元一次联立方程写出；解出假想弯矩之后，便可以求得网架的杆件内力。

此方法未知量数目较少，并且有图表可直接查用，便于计算，但是计算误差较大，目前少用。但可以作为初选杆件截面使用。

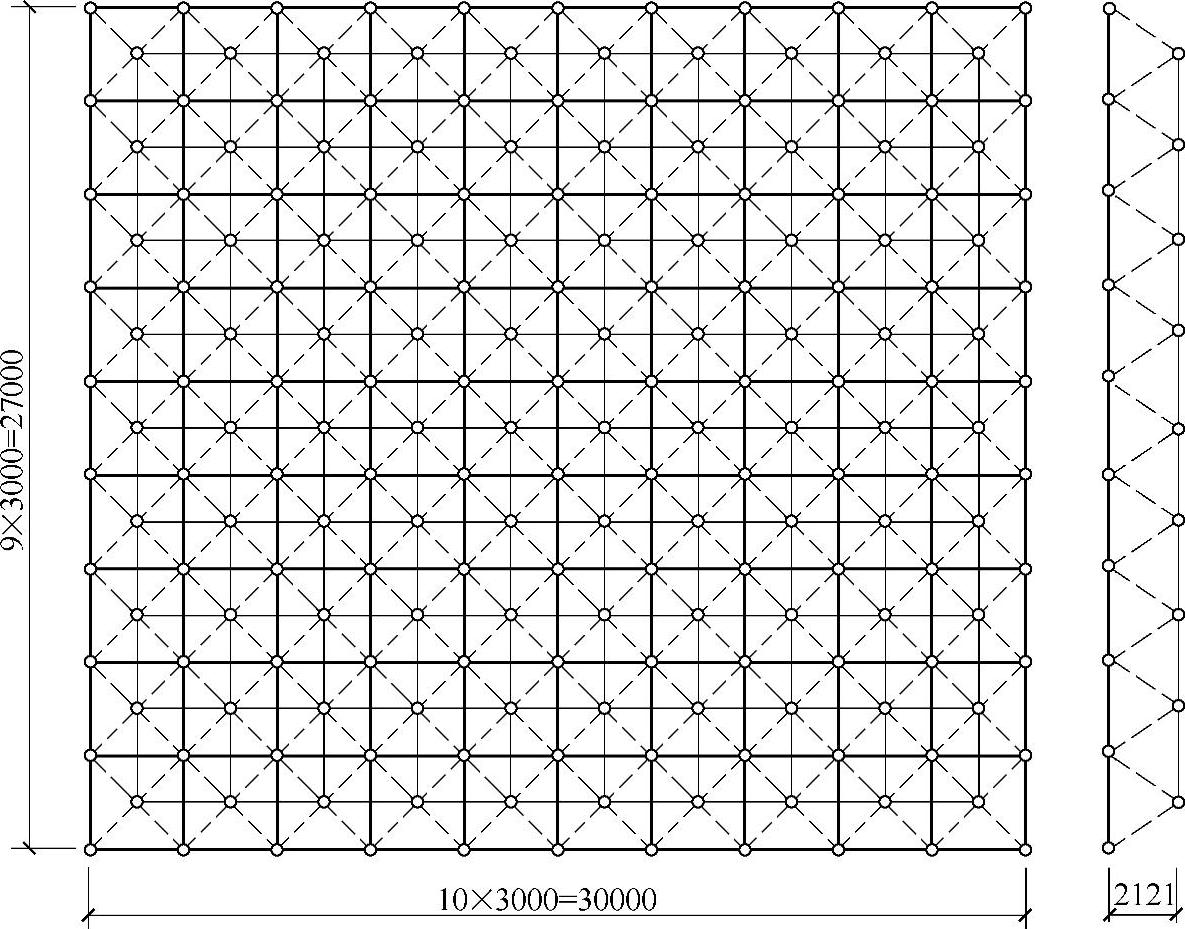
图7-98 网架平面布置图（例7-5）

【例7-5】 正放四角锥网架。网架平面尺寸27m×30m，周边支承。屋面材料为3.0m×3.0m发泡水泥复合板WB330-1，两面坡排水，屋面坡度4%，采用钢管支托找坡。杆件采用高频电焊钢管，节点为焊接空心球节点，钢材Q235，焊条E43型。网格尺寸为3m×3m；网架高度h=2.12m，跨高比L₂/h=12.73。上、下弦杆及腹杆的几何长度l均为3m，腹杆与上、下弦杆的夹角均为60°。网架平面布置如图7-98所示。试计算相关荷载和强度。

【解】 （1）荷载

1）永久荷载标准值。屋面板自重（包括板缝）0.6kN/m²，防水层0.10kN/m²，网架自重0.18kN/m²，悬挂设备0.1kN/m²。结构分析时，悬挂设备荷载均考虑作用在下弦节点。

2）可变荷载标准值。屋面均布活荷载与雪荷载的较大值为0.5kN/m²。

3）荷载组合。采用可变荷载效应控制的组合，即：1.2×永久荷载标准值+1.4×可变荷载标准值。

4）节点荷载设计值。

上弦节点：中间节点Q=[1.2×（0.6+0.1+0.18/2）×9+1.4×0.5×9]kN=14.83kN

端节点Q=[1.2×（0.6+0.1+0.18/2）×4.5+1.4×0.5×4.5]kN=7.42kN

下弦节点：中间节点Q=1.2×（0.1+0.18/2）×9kN=2.05kN

端节点Q=1.2×（0.1+0.18/2）×4.5kN=1.03kN

（2）杆件内力 根据空间桁架位移法编制的电算程序计算的杆件内力设计值如图7-99所示。

图7-99 杆件内力图（例7-5）

（3）杆件截面选择 杆件承载力设计值计算见表7-17；杆件截面选择如图7-100所示。

表7-17 杆件承载力设计值计算

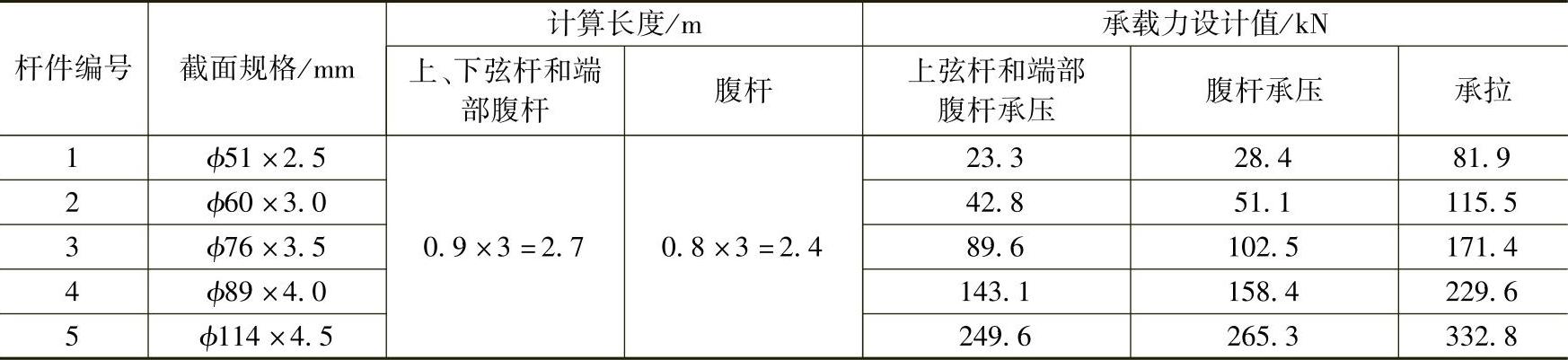
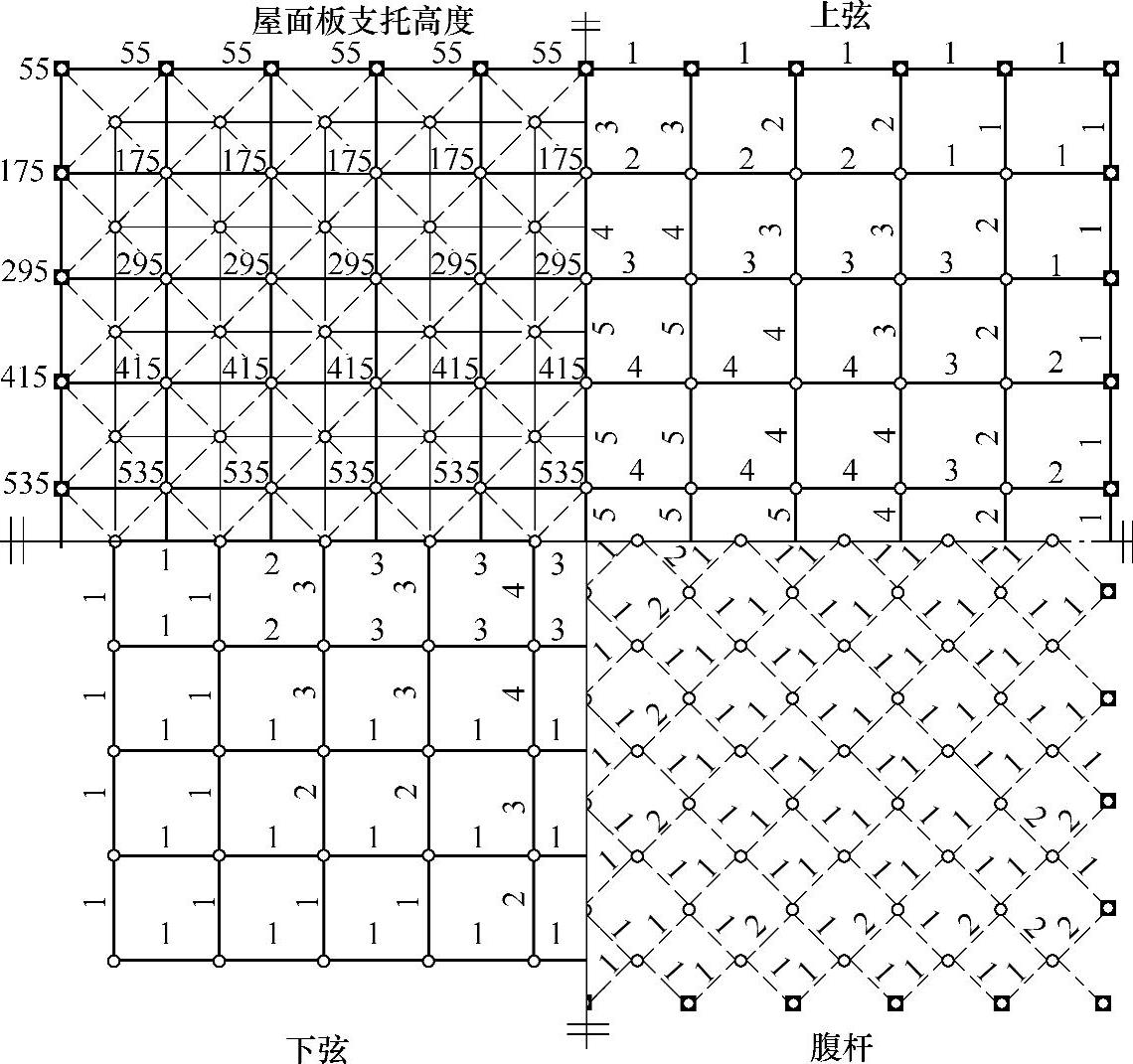
图7-100 杆件截面编号（例7-5）

（4）焊接钢球截面选择 采用不加肋的焊接空心球，根据杆件最大内力处弦杆与腹杆排列位置及夹角，初选钢球直径D=200mm，壁厚t=6mm。

按式（7-95）计算的空心球受压承载力设计值为

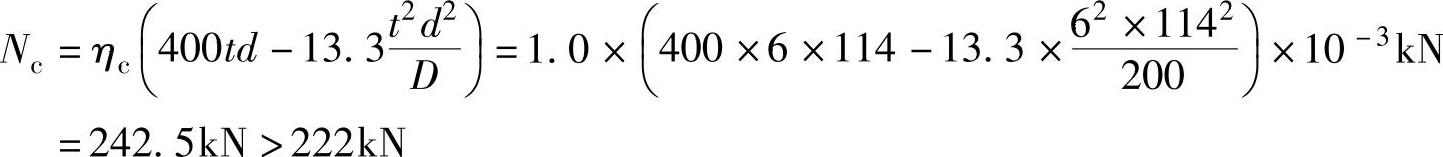
按式（7-96）计算的空心球受拉承载力设计值为

N_t=0.55η_ttdπf=0.55×1.0×6×114×π×215×10^-3kN=254.1kN＞222kN

按式（7-94）计算的空心球最小直径为

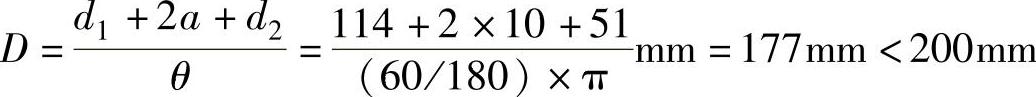
故所选D×t=200mm×6mm的焊接空心球，拉、压承载力均满足设计要求。

（5）节点连接计算 所有杆件均与焊接空心球采用等强度的坡口焊缝。支座节点设计从略。

（6）挠度 根据电算结果，理论挠度值为61.7mm＜L₂/250=108mm。