檩条形式较多，这里重点介绍目前常用的实腹式檩条的内力分析、强度、稳定性及刚度计算。

1.内力分析

实腹式檩条应按照在两个主轴平面内受弯的构件（双向弯曲梁）进行计算，即将均布荷载p分解为两个荷载分量p_x和p_y分别计算。

1）垂直于主轴x和y的分荷载（如图7-46所示）的计算式为

p_y=pcosα₀ （7-3）

p_x=psinα₀ （7-4）

式中 p——檩条竖向荷载设计值；

α₀——p与主轴y的夹角，对槽形和工字型截面α₀=α，α为屋面坡角；对Z形截面

α₀=｜θ-α｜，θ为主轴工与平行于屋面轴x₁的夹角。

2）檩条的弯矩可按以下规定计算。

①在刚度最大主平面（对x轴）由p_y引起的弯矩。

单跨简支构件：跨中最大弯矩M_x=p_yl²/8，l为檩条的跨度。

多跨连续构件：不考虑活荷载的不利组合，跨中和支座弯矩均近似取M_x=p_yl²/10。

②在刚度最小主平面（对y轴）由p_x引起的弯矩，按照简支梁或连续梁（设有拉条时，视拉条为檩条的侧向支承点）按以下规定计算。

a.檩间无拉条时，跨中弯矩M_y=-p_xl²/8

b.一根拉条位于l/2时，跨中负弯矩My=-pxl2/32。

c.两根拉条位于l/3时，l/3处负弯矩M_y=-p_xl²/90；跨中正弯矩M_y=p_xl²/360。

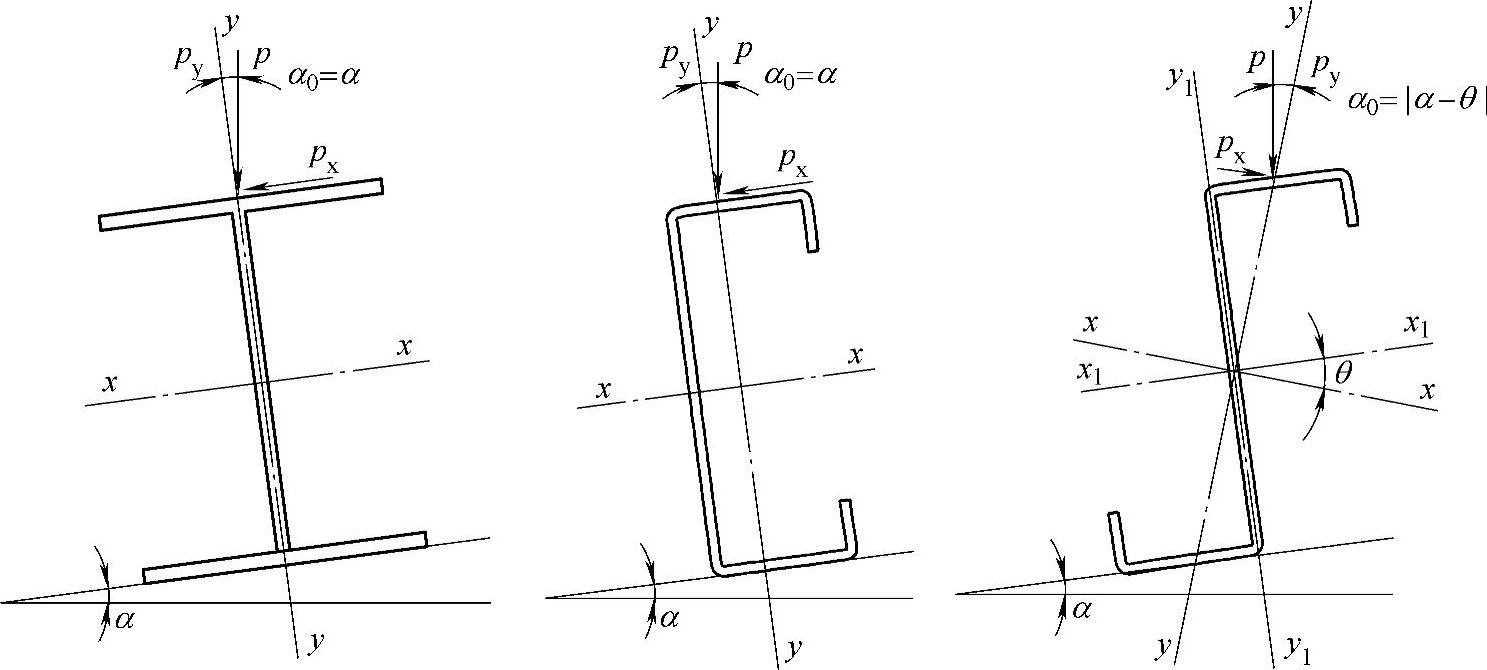
图7-46 实腹式檩条截面主轴和荷载示意图

2.强度计算

当屋面能够阻止檩条侧向失稳和扭转时，可不计算檩条的整体稳定性，仅按式（7-5）、式（7-6）计算其强度即可。

冷弯薄壁型钢：

热轧型钢：

式中 M_x、M_y——刚度最大主平面（由p_y引起）和刚度最小主平面（由p_x引起）的弯矩。当无拉条或设一根拉条时，采用檩条跨中的弯矩；当设两根拉条时，若p_x＞3.5p_y，采用檩条跨中弯矩；若p_x＜3.5p_y，采用1/3跨处的弯矩；

W_enx、W_eny——对主轴x、y的有效净截面模量；

W_nx、W_ny——主轴x、y的净截面模量；

γ_x、γ_y——截面塑性发展系数，按相关的规定采用；

f——钢材的强度设计值。

3.稳定计算

1）当屋面不能阻止檩条侧向失稳及扭转时，可按照下式计算檩条的稳定性。

冷弯薄壁型钢

热轧型钢

式中 W_ex、W_ey——对主轴x、y的有效截面模量；

W_x、W_y——对主轴x、y的毛截面模量；

φ_b——受弯构件绕强轴的整体稳定系数，按表4-5或表4-8选用；

φ_bx——受弯构件绕强轴的整体稳定系数，按式（7-9）～式（7-11）计算。

以上公式中，M_x与M_y当所验算点为压应力时取负号，为拉应力时取正号。

2）当檩条在永久荷载和风吸力组合下，下翼缘受压时：

①可偏安全地按照式（7-7）或式（7-8）计算檩条下翼缘受压、上翼缘受拉时的稳定；此时檩条可按跨中无侧向支承点考虑，取l_y=l₀（檩条下翼缘附近未设拉条时）即可。

②当屋面能够阻止檩条上翼缘侧向位移和扭转时，也可按照《门式刚架轻型房屋钢结构技术规程》（CECS 102—2002）附录E列出的考虑屋面对受拉上翼缘的约束对受压下翼缘的稳定进行计算。

③当风吸力较大时，为提高受压下翼缘的稳定，在檩条下翼缘附近允许增设拉条，如图7-15a中虚线所示，此时l_y应取其下翼缘的拉条间距。

④若仅为提高檩条下翼缘受压时的稳定，把檩条上翼缘拉条下移至下翼缘附近时，还需重新验算檩条在永久荷载与可变荷载组合下，由于受压上翼缘无拉条而使其平面外弯矩M_y增大对强度的不利影响，并采取临时措施确保檩条在安装时的稳定。

3）单轴或双轴对称截面的简支梁，当绕对称轴（x轴）弯曲时，其整体稳定系数φ_bx应按照式（7-9）～式（7-11）进行计算。

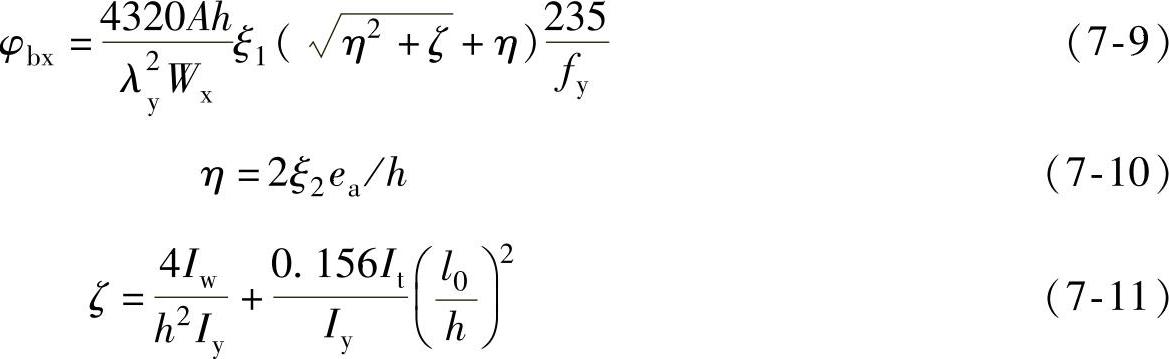
式中 λ_y——梁在弯矩作用平面外的长细比；

A——毛截面面积；

h——截面高度；

l₀——梁的侧向计算长度，计算式为

l₀=μ_bl

μ_b——梁的侧向长度计算系数，按表7-6采用；

l——梁的跨度；

ξ₁、ξ₂——系数，按表7-4采用；

e_a——横向荷载作用点到截面弯心的距离，对于偏心压杆或当横向荷载作用在弯心时，e_a=0；当荷载不作用在弯心且荷载方向指向弯心时，e_a为负，而离开弯心时e_a为正；

W_x——对x轴的受压边缘毛截面截面模量；

I_w——毛截面扇性惯性矩；

I_y——对y轴的毛截面惯性矩；

I_t——扭转惯性矩；

表7-4 两端及跨间侧向均为简支的受弯构件的ξ₁、ξ₂和μb

若按式（7-9）计算的φ_bx值大于0.7时，则应以φ′_bx代替φ_bx，φ′_bx计算式为

4）在式（7-5）和式（7-7）中，对薄壁型钢檩条的有效截面模量按下列规定确定。

①加劲板件、部分加劲板件和非加劲板件的有效宽厚比应按式（7-13）～式（7-15）计算。

当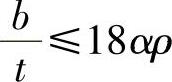时，

当时，

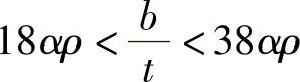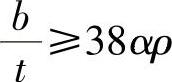当时，

式中 b——板件宽度；

t——板件厚度；

b_e——板件有效宽度；

α——计算系数，α=1.15-0.15ψ，当ψ＜0时，取α=1.15；

b_c——板件受压区宽度，当ψ≥0时，b_c=b；当ψ＜0时，b_c=b/（1-ψ）；

ψ——压应力分布不均匀系数，ψ=σ_min/σ_max；

σ_max——受压板件边缘的最大压应力（N/mm²），取正值；

σ_min——受压板件另一边缘的应力（N/mm²），以压应力为正，拉应力为负；

ρ——计算系数，

k——板件受压稳定系数；

k₁——板组约束系数，若不计相邻板件的约束作用，可取k₁=1.0。

式（7-16）中σ₁按下列规定确定。

a.在轴心受压构件中应依据由构件最大长细比所确定的稳定系数和钢材强度设计值的乘积（φf）作为σ₁。

b.对于压弯构件，截面上各板件的压应力分布不均匀系数ψ应根据构件毛截面按照强度计算，不考虑双力矩的影响。最大压应力板件的σ₁，取钢材的强度设计值f，其余板件的最大压应力根据ψ推算。

c.对于受弯及拉弯构件，截面上各板件的压应力分布不均匀系数ψ及最大压应力应由构件毛截面按强度计算，并不考虑双力矩的影响。

②受压板件的稳定系数k可按式（7-17）～式（7-24）计算。

a.加劲板件。

（a）当1≥ψ＞0时， k=7.8-8.15ψ+4.35ψ² （7-17）

（b）当0≥ψ≥-1时， k=7.8-6.29ψ+9.78ψ² （7-18）

b.部分加劲板件。

（a）最大压应力作用于支承边（图7-47a）：

当ψ≥-1时， k=5.89-11.59ψ+6.68ψ² （7-19）

（b）最大压应力作用于部分加劲边（图7-47b）

当ψ≥-1时， k=1.15-0.22ψ+0.045ψ² （7-20）

c.非加劲板件。

（a）最大压应力作用于支承边（图7-47c）：

当1≥ψ＞0时， k=1.70-3.025ψ+1.75ψ² （7-21）

当0≥ψ＞-0.4时， k=1.70-1.75ψ+55ψ² （7-22）

当-0.4≥ψ≥-1时，k=6.07-9.51ψ+8.33ψ² （7-23）

（b）最大压应力作用于自由边（图7-47d）：

当ψ≥-1时，k=0.567-0.213ψ+0.07ψ² （7-24）

当ψ＜-1时，以上各式的k值按ψ=-1的值采用。

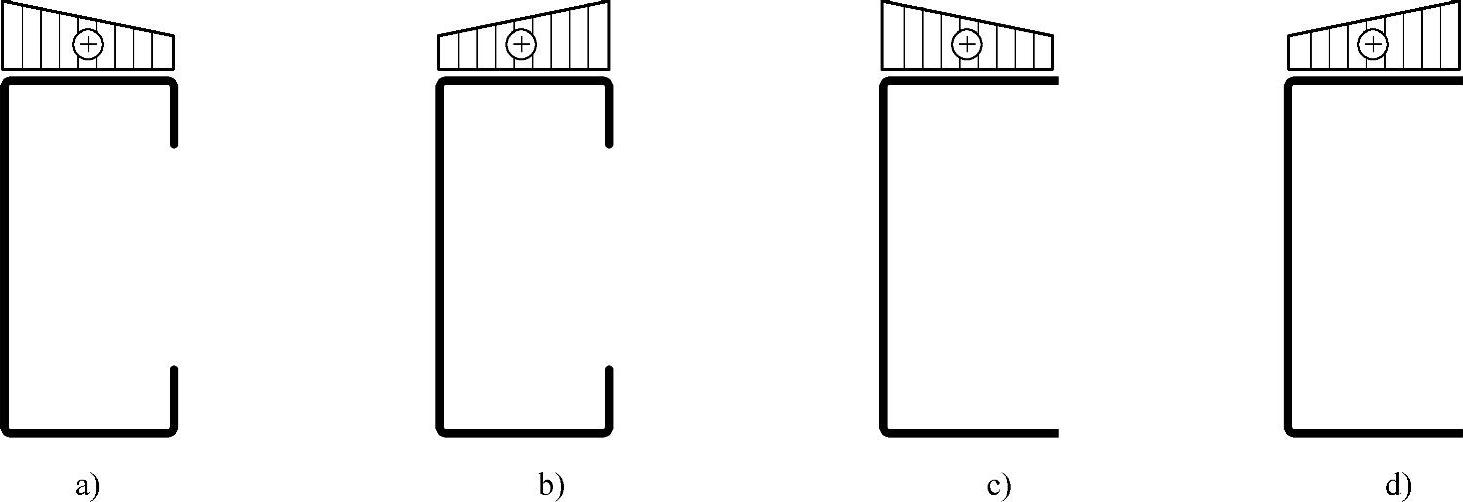
图7-47 部分加劲板和非加劲板的应力分布示意图

③受压板件的板组约束系数k₁应按式（7-25）～式（7-27）计算。

当ξ≤1.1时，

当ξ＞1.1时，k₁=0.11+0.93/（ξ-0.05）2（7-26）(www.daowen.com)

式中 b——计算板件的宽度；

c——与计算板件邻接的板件宽度；如果计算板件两边均有邻接板件时，即计算板件为加劲板件时，取压应力较大一边的邻接板件宽度；

k——计算板件的受压稳定系数；

k_c——邻接板件的受压稳定系数。

当k₁＞k′₁时，取k₁=k′₁，k₁为k′₁的上限值。对于加劲板件k′₁=1.7；对于部分加劲板件k′₁=2.4；而对于非加劲板件，则k′₁=3.0。

当计算板件只有一边有邻接板件，也就是在计算板件为非加劲板件或部分加劲板件，且邻接板件受拉时，取k₁=k′₁。

④部分加劲板件中卷边的高厚比不宜大于12，卷边的最小高厚比应依据部分加劲板件的宽厚比按表7-5来采用。

表7-5 卷边的最小高厚比

注：a为卷边的高度；b为带卷边板件的宽度；t为板厚。

⑤当受压板件的宽厚比大于式（7-13）～式（7-15）所规定的有效宽厚比时，受压板件的有效截面应自截面的受压部分按照图7-48所示位置扣除其超出部分来确定（即图中带斜线部分），截面的受拉部分全部有效。

图7-48中的b_e1和b_e2按下列规定计算。

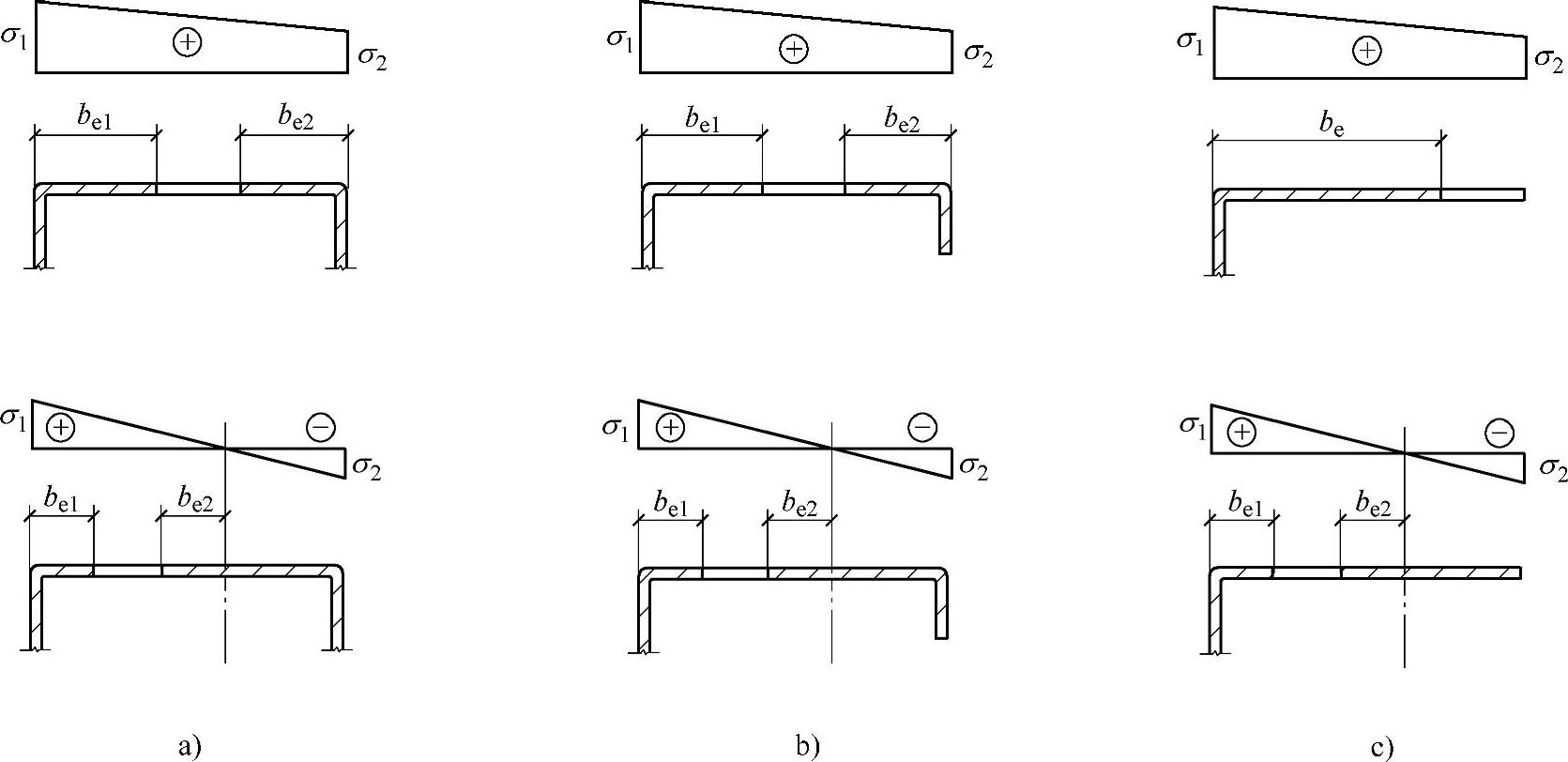
图7-48 受压板件的有效截面图

a）加劲板件 b）部分加劲板件 c）非加劲板件

a.对于加劲板件：当ψ≥0时，b_e1=2b_e/（5-ψ）b_e2=b_e-b_e1；当ψ＜0时，b_e1=0.4b_eb_e2=0.6b_e。

b.对于部分加劲板件和非加劲板件：b_e1=0.4b_eb_e2=0.6b_e。

c.b_e按式（7-13）～式（7-15）确定。

⑥圆管截面构件的外径与壁厚之比，当采用Q235钢时不宜大于100；采用Q345钢时不宜大于68，此时在计算中可取其截面全部有效。

4.变形计算

为使屋面较平整，实腹式檩条应验算与屋面垂直方向的挠度，对无积灰的瓦楞铁和石棉瓦屋面，其容许挠度值[v]=l/150；对于有积灰的瓦楞铁和石棉瓦屋面、压型钢板、发泡水泥复合板、钢丝网水泥瓦以及其他水泥制品瓦材屋面，其容许挠度值[v]=l/200，l为檩条的跨度。

对两端简支檩条的挠度可按照式（7-28）进行计算。

式中 p_ky——沿轴线荷载的标准值；

I_x——对主轴x的毛截面惯性矩。

对Z型钢垂直屋面方向的挠度v_y1可按照式（7-29）进行计算。

式中 α——为屋面坡角；

I_x1——对平行于屋面轴x₁的毛截面惯性矩。

【例7-1】 轻型槽钢檩条。屋面材料为石棉水泥波形瓦，干铺油毡一层，20mm厚木望板，屋面坡度1/2.5（a=21.80°），檩条跨度6m，于跨中设一道拉条，水平檩距0.75m，沿坡向斜距0.808m。钢材Q235。其中，永久荷载：石棉瓦等（含防水及木基层）0.37kN/m²，檩条（包括拉条、支撑）自重设为0.1kN/m；可变荷载采用0.50kN/m²。试计算内力和强度。

【解】（1）内力计算

1）檩条线荷载：

p_k=（0.37×0.808+0.1+0.50×0.75）kN/m=0.774kN/m

p=[1.2×（0.37×0.808+0.1）+1.4×0.50×0.75]kN/m=1.004kN/m

p_x=psin21.80°=0.373kN/m

p_y=pcos21.80°=0.932kN/m

2）弯矩设计值：

M_x=pyl²/8=0.932×6²/8kN·m=4.19kN·m

M_y=p_xl²/32=0.373×6²/32kN·m=0.42kN·m

（2）截面选择及强度计算 选用轻型槽钢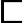10，如图7-49所示。W_x=34.8cm³，W_ymax=14.2cm³，W_ymin=6.5cm³，I_x=173.9cm⁴，i_x=3.99cm，i_y=1.37cm。

计算截面有孔洞削弱，考虑0.9的折减系数，则净截面模量为

W_nx=0.9×34.8cm³=31.32cm³

W_nymax=0.9×14.2cm³=12.78cm³

W_nymin=0.9×6.5cm³=5.85cm³

屋面能够阻止檩条失稳及扭转，截面的塑性发展系数γ_x=1.05，γ_y=1.20，根据受弯构件强度计算公式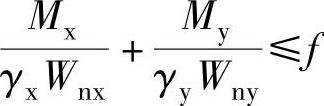，计算截面a、b点的强度为

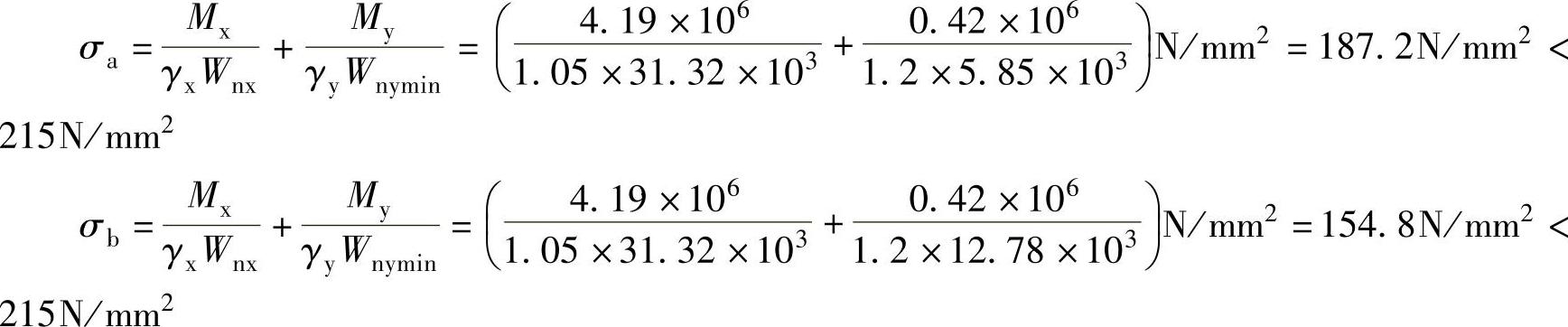
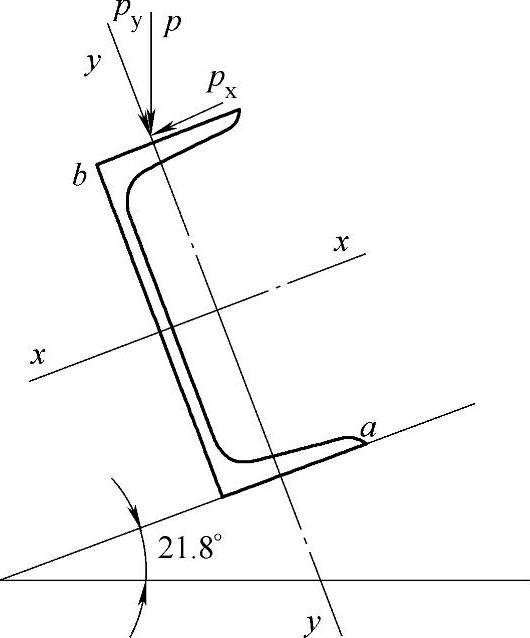
图7-49 檩条截面力系示意图（例7-1）

（3）挠度计算 按式（7-28）计算的挠度为

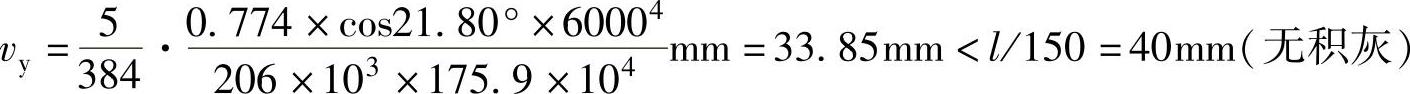
（4）构造要求

λ_x=600/3.99=150.4＜200

λ_y=300/1.37=219.0＞200

故此檩条不可兼作屋面平面内的支撑竖杆或刚性系杆，只可兼作柔性系杆。

【例7-2】 冷弯薄壁卷边槽钢檩条（风吸力控制）。封闭式建筑，屋面材料为压型钢板，屋面坡度1/10（α=5.71°），檩条跨度6m，于l/2处设一道拉条；水平檩距1.50m。檐口距地面高度8m，屋脊距地面高度9.2m。钢材Q235。永久荷载：压型钢板（单层无保温）自重为0.12kN/m²，檩条（包括拉条）自重设为0.05kN/m²。可变荷载：屋面均布活荷载或雪荷载最大值为0.50kN/m²。基本风压w₀=0.40kN/m²，地面粗糙度类别B类。试计算内力及设计强度。

【解】

（1）内力计算

1）永久荷载与屋面活荷载组合。

檩条线荷载：

p_k=（0.17+0.50）×1.5kN/m=1.005kN/m

p=（1.2×0.17+1.4×0.50）×1.5kN/m=1.356kN/m

p_x=psin5.71°=0.135kN/m

p_y=pcos5.71°kN/m=1.349kN/m

弯矩设计值：

M_x=p_yl²/8=1.349×6²/8kN·m=6.07kN·m；

M_y=p_xl²/32=0.135×6²/32kN·m=0.15kN·m

2）永久荷载与风荷载吸力组合

按《建筑结构荷载规范》（GB 50009—2012），房屋高度小于10m，风荷载高度变化系数取10m高度处的数值，μ_z=1.0。按《门式刚架轻型房屋钢结构技术规程》（CECS 102—2002）附录A，风荷载体型系数为1.5lgA-2.9=-1.47（边缘带），A=1.5×6m²=9m²。

垂直屋面的风荷载标准值：

w_k=μs·μz·w0=-1.47×1.0×（1.05×0.4）kN/m²=-0.617kN/m²

檩条线荷载：

p_ky=（0.617-0.17×cos5.71°）×1.5kN/m=0.646kN/m

p_x=0.17×1.5×sin5.71°kN/m=0.025kN/m

p_y=（1.4×0.617×1.5-0.17×1.5×cos5.71°）kN/m=1.04kN/m

弯矩设计值（采用受压下翼缘不设拉条的方案）：

M_x=p_yl²/8=1.04×6²/8kN·m=4.68kN·m

M_y=p_xl²/32=0.025×6²/32kN·m=0.03kN·m

截面选用160×70×20×3.0，如图7-50a所示。

A=9.45cm²，W_x=46.71cm³，W_ymax=27.17cm³，W_ymin=12.65cm³

I_x=373.64cm⁴，I_y=60.42cm⁴，I_t=0.2836cm⁴，I_w=3070.5cm⁶

i_x=6.29cm，i_y=2.53cm.x₀=2.22cm，e₀=5.25cm

（2）强度计算

1）有效净截面模量。在腹板的计算截面有一ϕ13拉条连接孔，距上翼缘板边缘35mm，如图7-50b所示，则有效净截面模量为

图7-50 檩条内力及设计强度计算示意图（例7-2）

a）檩条截面力系示意图 b）檩条有效截面示意图

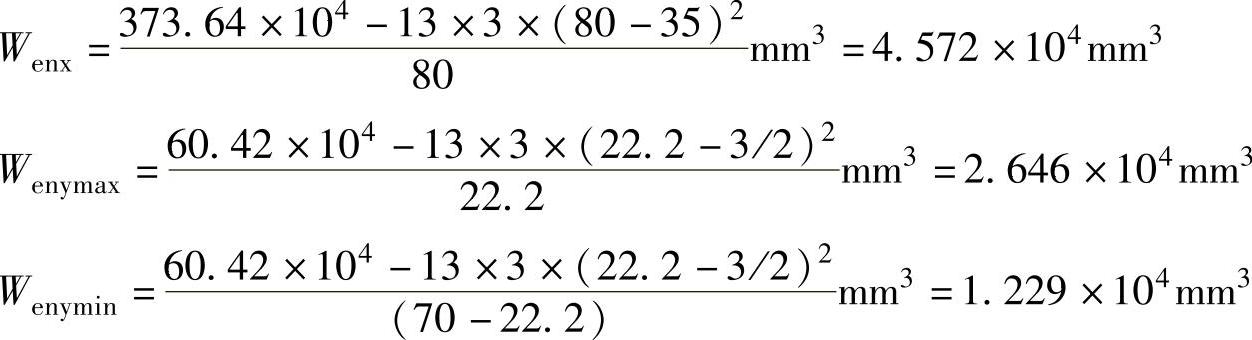
2）屋面能阻止檩条侧向失稳和扭转，按式（7-5）计算①、④点的强度为

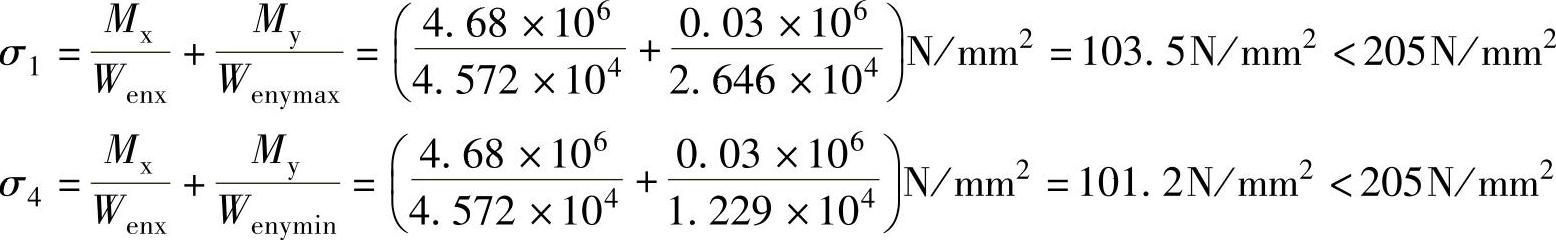
（3）稳定计算

1）有效截面模量。永久荷载与风吸力组合下的弯矩小于永久荷载与屋面可变荷载组合下的弯矩，根据前面的计算结果，截面全部有效；同时不计孔洞削弱，则W_ex=W_x=46.71cm³，W_ey=W_eymin=12.65cm³。

2）受弯构件的整体稳定系数φ_bx按式（7-9）～式（7-12）计算。

查表7-6，跨中无侧向支承，μ_b=1.0，ξ₁=1.13，ξ₂=0.46。

e_a=h/2=16/2mm=8.0mm（取正值）

η=2ξ₂e_a/=2×0.46×8.0/16=0.46

3）风吸力作用使檩条下翼缘受压，按式（7-7）计算的稳定性为

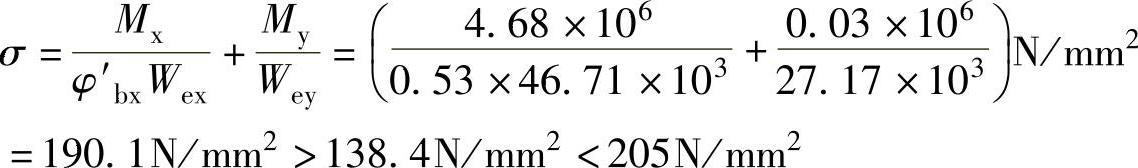
计算表明由永久荷载与风荷载组合控制。以上计算未考虑屋面对上翼缘的约束，若考虑这一因素，可将公式中屋面自重在y方向的分量忽略，即认为在y方向产生的弯矩全部由受拉翼缘承受。

（4）挠度计算 按式（7-29）计算的挠度为

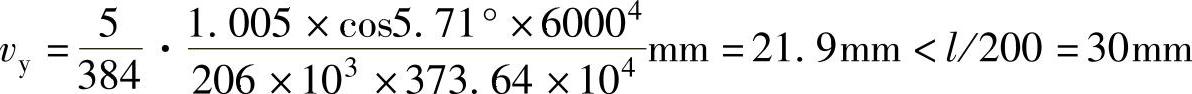
（5）构造要求

λ_x=600/6.29=95

λ_y=300/2.53=119＜200

故此檩条在平面内、外均满足要求。