不允许板件发生局部失稳的保证是令局部屈曲临界应力大于钢材屈服强度或大于构件的整体稳定临界应力。为了保证压弯构件中板件的局部稳定，规范采取了限制翼缘和腹板的宽厚比及高厚比的方法。宽厚比限值中的截面尺寸如图5-9所示。

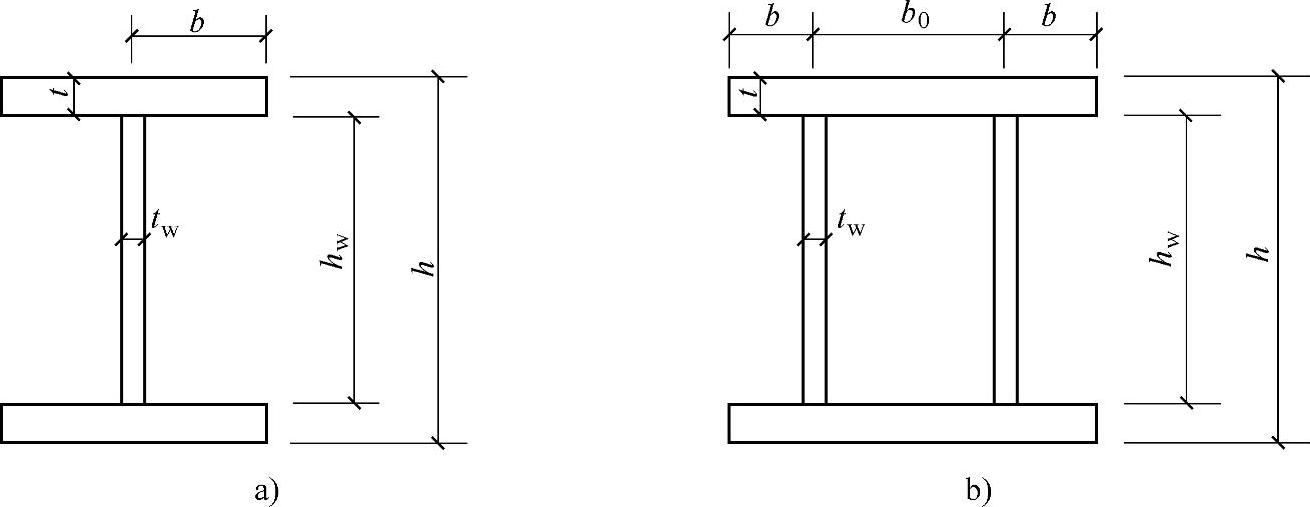
图5-9 宽厚比限值中的截面尺寸

1.翼缘的宽厚比

压弯构件的受压翼缘板，其应力情况与梁受压翼缘基本相同。因此，压弯构件翼缘宽厚比的限值按式（5-30）、式（5-31）计算

外伸翼缘板：

若考虑截面的有限塑性发展，则b/t≤13235/f_y

两边支撑翼缘板：

2.腹板的高厚比

压弯构件腹板的高厚比限值，按不同截面形式分别规定如下。

（1）工字形截面

工字形截面腹板的局部失稳，是在不均匀压应力和剪应力的共同作用下发生的，可以引入两个系数来表述两者的影响。

应力梯度：

式中 σ_max——腹板计算高度边缘的最大压应力，计算时不考虑构件的稳定系数和截面塑性发展系数；

σ_min——腹板计算高度另一边缘相应的应力，压应力取正值，拉应力取负值。

与剪应力有关的系数：

对压弯构件，腹板中剪应力τ的影响不大，经分析，平均剪应力可取腹板弯曲正应力的0.3倍，一般可取β₀=0.3。腹板弹性屈曲临界应力为

式中 K_e——弹性屈曲系数，其值与应力梯度α₀有关，见表5-1。

压弯构件失稳时，截面的塑性变形将不同程度地发展。腹板的塑性发展深度与构件的长细比λ和板的应力梯度α₀有关，腹板的弹塑性临界应力为

式中 K_p——塑性屈曲系数，当β₀=0.3，截面塑性深度为0.25h_w时，其值见表5-1。

表5-1 压弯构件中腹板的屈曲系数和高厚比h_w/tw

对于长细比较小的压弯构件，整体失稳时截面的塑性深度实际上已超过0.25h_w；对于长细比较大的压弯构件，截面的塑性深度则不到0.25h_w，甚至腹板受压最大的边缘还没有屈服。因此，腹板高厚比限值宜随长细比的增大而适当放大。同时，当α₀=0时，应与轴心受压构件腹板高厚比的要求相一致；而当α₀=2时，应与受弯构件中考虑了弯矩和剪力联合作用的腹板高厚比的要求相一致。根据这些因素，得到的腹板高厚比限值是参数α₀、λ的复杂函数。用直线方程加以简化，可以得到式（5-36）、式（5-37）。

当0≤α₀≤1.6时：(www.daowen.com)

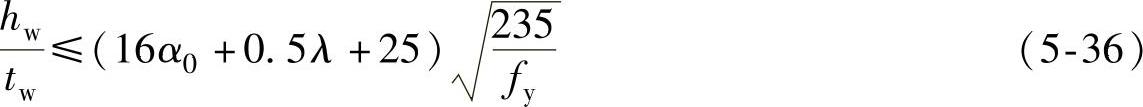
当1.6＜α₀≤2时：

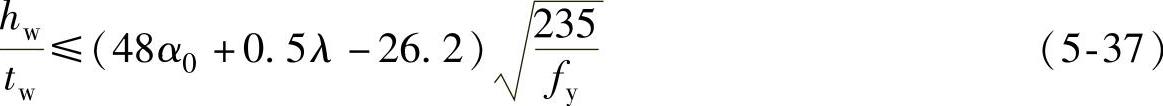
式中 λ——构件在弯矩作用平面内的长细比，当λ＜30时，取λ=30；当λ＞100时，取λ=100

（2）箱形截面 考虑箱形截面两腹板受力可能不一致，而且翼缘与腹板常用单侧角焊缝连接，其约束作用也不如工字形截面。因此，箱形截面的h_w/t_w不应大于式（5-36）和式（5-37）右边计算值的0.8倍；当此值小于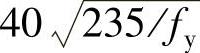时，取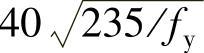

（3）T形截面

1）弯矩使腹板自由边受拉：

热轧剖分T型钢

焊接T型钢

2）弯矩使腹板自由边受压：

当α₀≤1.0时

当α₀＞1.0时

（4）圆管截面

【例5-4】 如图5-10所示某压弯构件，承受轴向压力F=750kN，弯矩M=400kN·m，钢材为Q235，并已知λ_x=33.3，A=151cm²，I_x=133296cm⁴。试验算此构件的局部稳定。

【解】 （1）腹板的高厚比 腹板上下边缘应力：

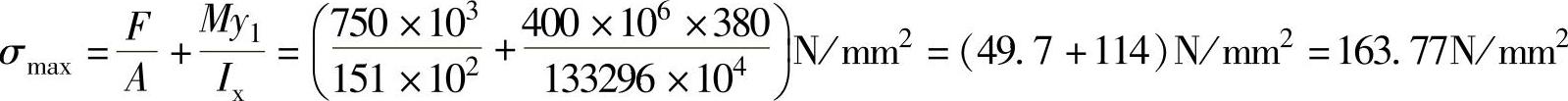
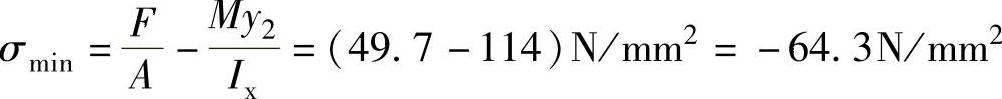
应力梯度：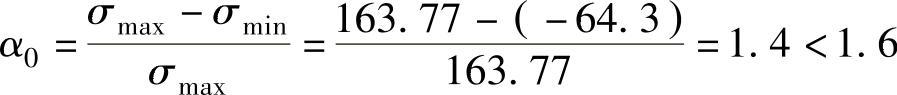

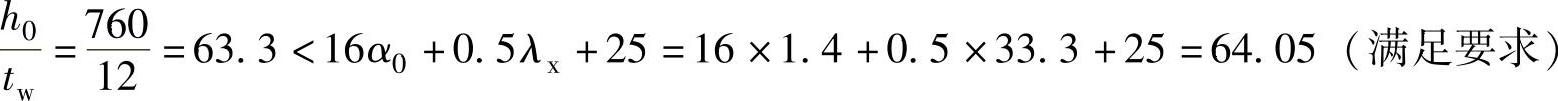
（2）翼缘宽厚比

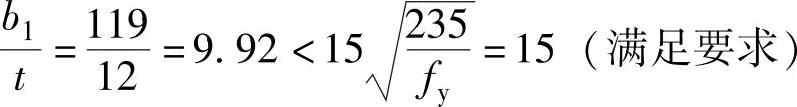
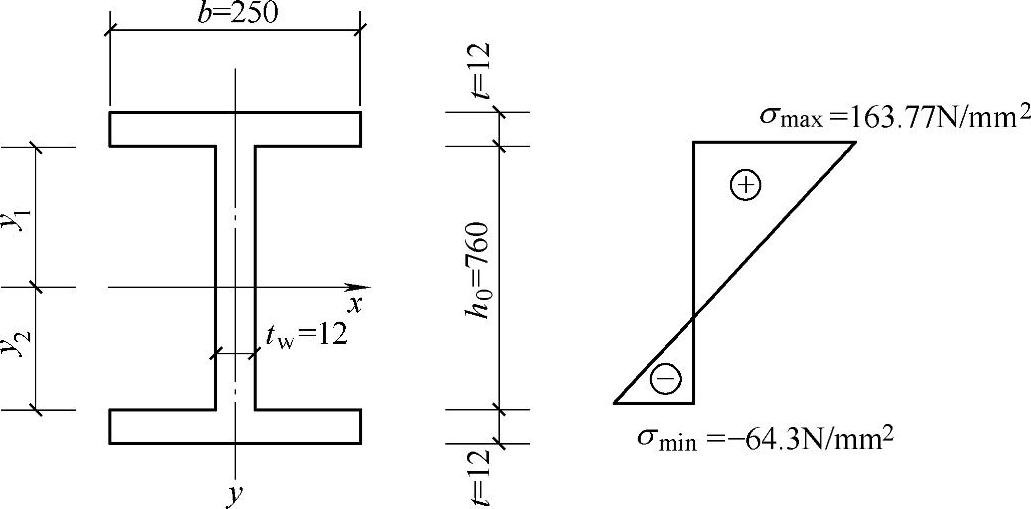
图5-10 压弯构件（例5-4）