为获得经济的截面尺寸，焊接钢梁常增大翼缘的宽厚比和腹板的高厚比。受压翼缘和轴心受压构件一样，受到较均匀的压应力。腹板中段受到较大的纵向压应力，端部腹板受到剪力引起的斜压应力，都有可能使各板件失去稳定。丧失局部稳定后虽不如丧失整体稳定立即导致梁失去承载能力的后果那样严重，但局部失稳会改变梁的受力状况，降低梁的刚度和整体稳定性，所以局部稳定性的问题必须认真对待。

1.翼缘板的容许宽厚比

梁的翼缘板远离截面形心，强度能得到比较充分的利用，且受压翼缘板受到较均匀的纵向压应力，所以可以用限制宽厚比的方法来保证它不先于梁的整体失稳。

规范规定，在弹性工作范围内，梁受压翼缘的自由外伸宽度b₁与其厚度t之比应满足式（4-19）。

简支梁截面允许出现部分塑性，即式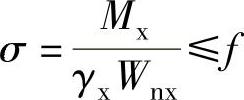中取γ=1.05时，梁翼缘自由外伸宽度b₁和其厚度t之比是

2.腹板加劲肋的设置

腹板应力分布不均匀，大部分应力很低，中和轴以下为拉应力，如果也用限制高厚比的方法来控制其局部稳定是不经济的。提高梁腹板的局部稳定常用设置加劲肋来完成，如图4-11所示。

加劲肋可分为横向、纵向、短加劲肋和支撑加劲肋。支撑加劲肋用于承受固定集中力（如支座反力），它和横向加劲肋在梁腹板中常设置；纵向加劲肋和短加劲肋不是所有梁中都有。

不考虑腹板屈曲后强度的利用，下面讨论梁腹板加劲肋的配置、计算和有关构造。

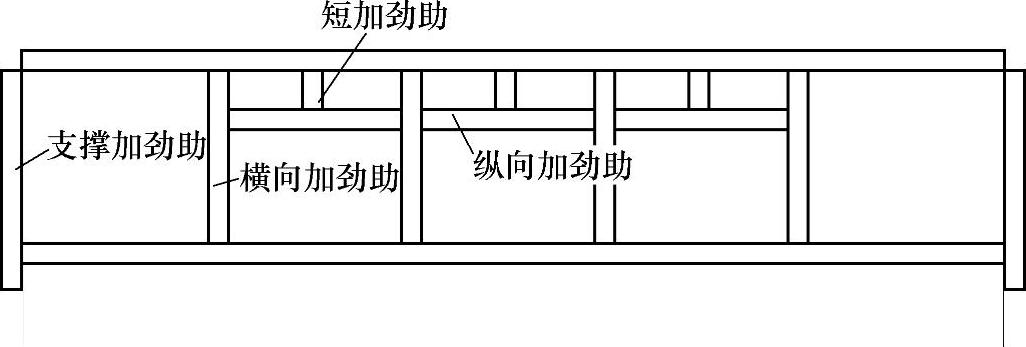
图4-11 腹板加劲肋的配置

（1）腹板加劲肋的配置 如图4-11所示。

1）对于腹板高厚比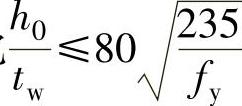的梁，无局部压应力（σ_cr=0）时，可不配置横向加劲肋。有局部压应力（σ_c≠0）时，按构造配置横向加劲肋，加劲肋间距a应满足0.5h₀≤a≤2h₀。

2）对于满足式（4-21）的梁，应配置横向加劲肋，并要按下面的方法计算区格内的局部稳定。

3）对于满足式（4-22）的梁，（2）中配置横向加劲肋后还要配置纵向加劲肋，并要按下面第（2）款中的方法计算区格内的局部稳定。

4）梁的支座处和上翼缘有固定集中力处应配置支撑加劲肋，对支撑加劲肋要进行计算。

（2）腹板加劲肋配置的计算 配置腹板加劲肋时，一般需要先根据构造要求进行加劲肋的布置，然后验算，必要时再调整。验算局部稳定的公式如下。

1）仅配置横向加劲肋的腹板（图4-12a），各区格应满足相关方程式（4-23）。

式中 σ——计算的区格内，由平均弯矩产生的腹板计算高度边缘的弯曲压应力，即

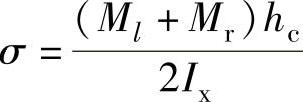
h_c——腹板受压区的高度；

M_l、M_r——区格左、右边缘的弯矩值；

I_x——截面的惯性矩；

τ——计算腹板区格内，由平均剪力V产生的腹板平均剪应力，即

σ_cr——在纯弯曲作用下的临界应力；

τ_cr——在纯剪切作用下的临界应力。

式（4-24）中的σ_cr、τ_cr是根据《钢结构设计规范》（GB 50017—2003），取国际上现行的通用高厚比λ_b、λ_s作为参数计算的。

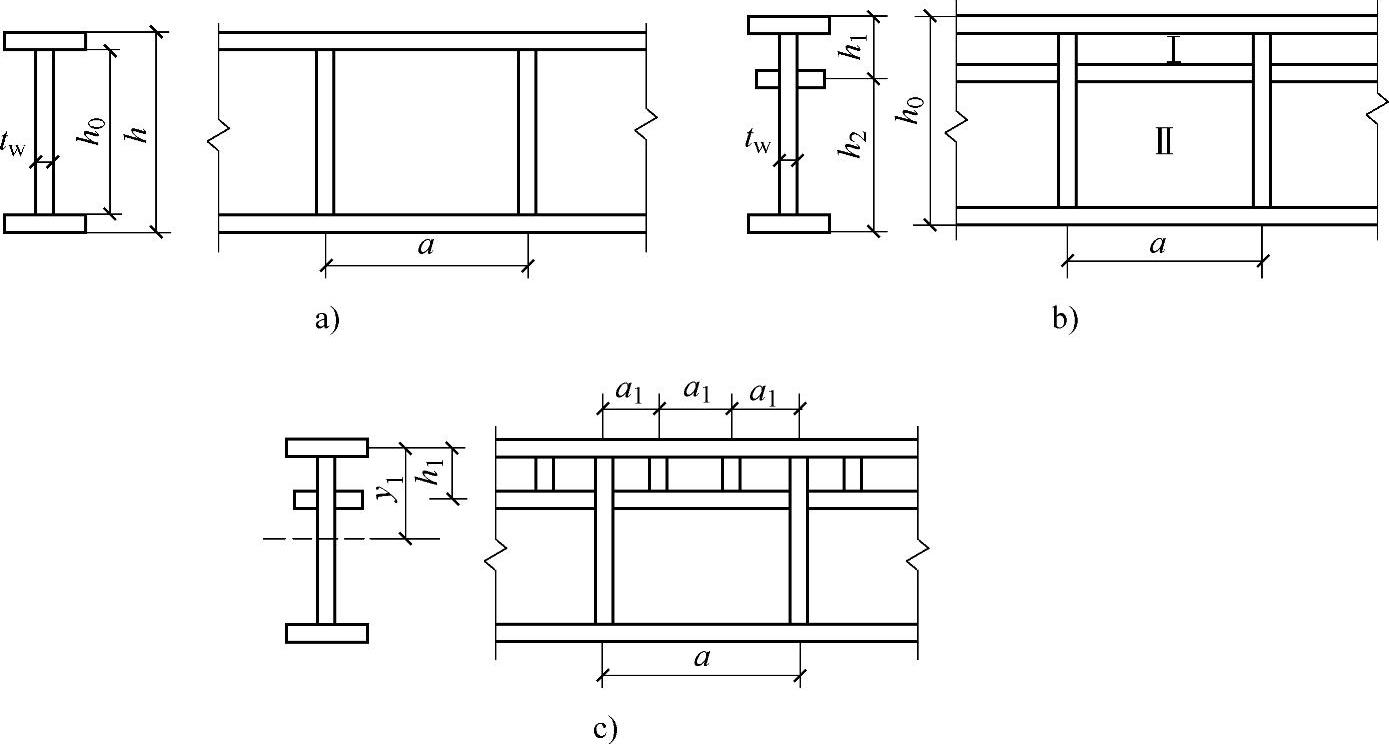
图4-12 腹板加劲肋布置

a）仅配置横向加劲肋模板 b）、c）同时配置横向加劲肋和纵向加劲肋区的模板

①纯弯曲通用高厚比λ_b按式（4-25）、式（4-26）计算，则临界应力σ_cr按式（4-27）计算。

受压翼缘扭转受到约束：

受压翼缘扭转未受约束：

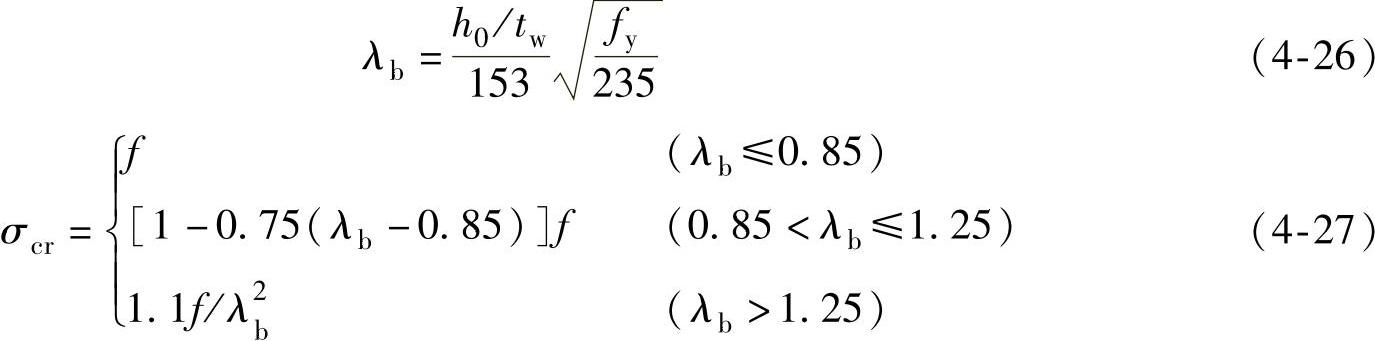
②纯剪切通用高厚比λ_s按式（4-28）、式（4-29）计算，则临界应力τ_cr按式（4-30）计算。

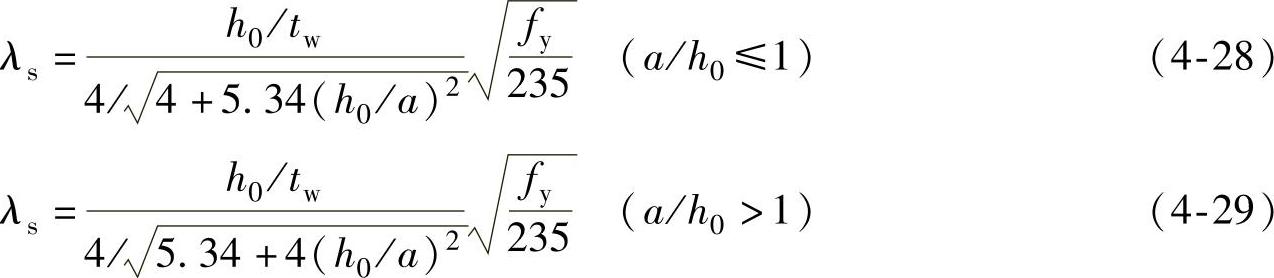
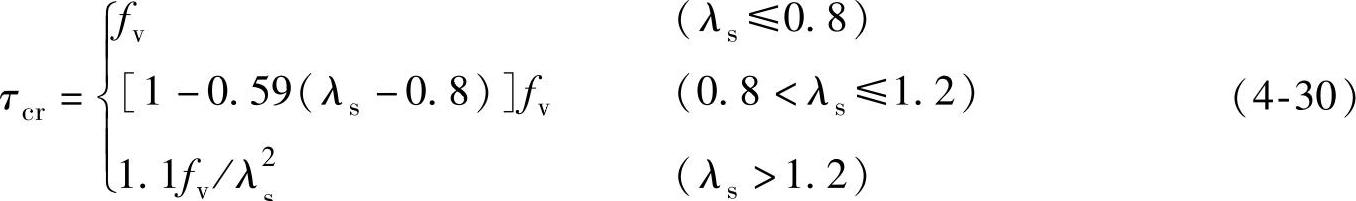
2）同时配置横向加劲肋和纵向加劲肋区格局部稳定的验算。

①受压翼缘和纵向加劲肋间区格Ⅰ的局部稳定的验算，如图4-12b所示。验算相关公式为

式中 σ、τ——区格Ⅰ的平均弯矩产生的腹板在计算高度边缘的弯曲压应力和平均剪应力。

σ_cr——按式（4-25）～式（4-27）计算，式中λ_b用λ_b1代替，即

受压翼缘扭转受到约束：

受压翼缘扭转未受约束：

h₁——对于双轴对称截面h₁=（0.2～0.25）h；

τ_cr——按式（4-28）～式（4-30）计算，式中h₀用h₁代替。

②纵向加劲肋和受拉翼缘间区格Ⅱ的局部稳定验算。验算相关公式为

式中 σ₂——区格Ⅱ平均弯矩产生的腹板在纵向加劲肋处的弯曲压应力；

τ——平均剪应力

σ_cr——按式（4-25）～式（4-27）计算，式中λ_b用λ_b2代替，即

h₂——h₂=h₀-h₁；(www.daowen.com)

τ_cr——按式（4-28）～式（4-30）计算，式中h₀用h₂代替。

（3）腹板加劲肋的构造要求 腹板加劲肋是为加强腹板的局部稳定而设置的。焊接梁的加劲肋一般用钢板做成，常在腹板两侧成对配置（图4-13a）。对于仅受静荷载作用或受动荷载作用较小的梁腹板，为了节省钢材和减轻制造工作量，其横向和纵向加劲肋亦可考虑单侧配置（图4-13b），但是对于支撑加劲肋不能单侧配置。

加劲肋作为腹板的支撑边，应有足够的刚度，为此要求：

1）在腹板两侧成对配置的钢板横向加劲肋，其截面尺寸按经验公式（4-36）和式（4-37）确定。

外伸宽度：

b_s≥h₀/30+40（mm） （4-36）

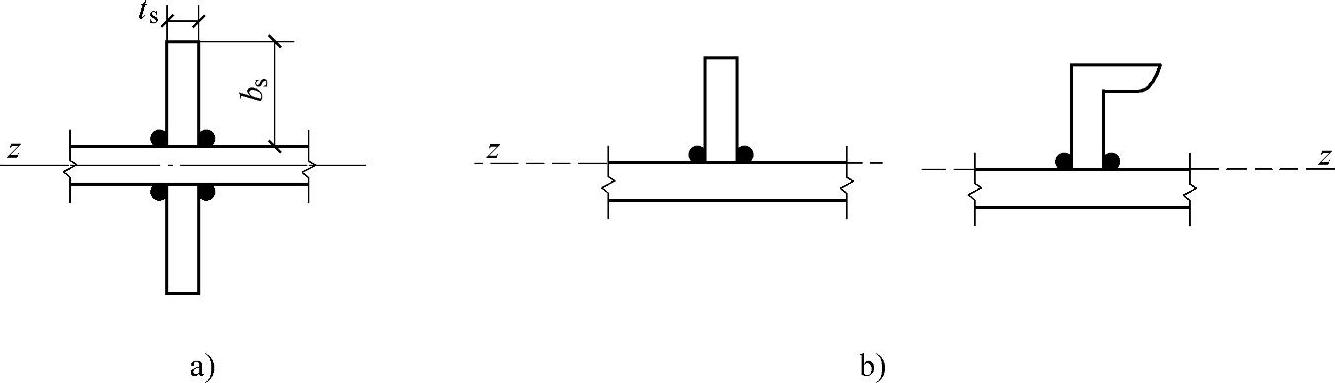
图4-13 加劲肋形式

a）腹板加劲肋在腹板两侧成对配置 b）腹板加劲肋在腹板单侧成对配置

厚度：

t_s≥b_s/15 （4-37）

2）仅在腹板一侧配置的钢板横向加劲肋，其外伸宽度应取式（4-36）算得值的1.2倍，厚度由式（4-37）计算。

3）在同时用横向加劲肋和纵向加劲肋加强的腹板中，横向加劲肋作为纵向加劲肋的支撑，所以应在其相交处将纵向加劲肋断开，横向加劲肋保持连续（图4-14a）。此时，横向加劲肋的截面尺寸除应满足上述要求外，其绕z轴的惯性矩还应满足式（4-38）。

I_x≥3h₀t³_w （4-38）

当加劲肋单向配置时，I_x应以和加劲肋相连的腹板边缘（如图4-14b所示中的z—z线）为轴线进行计算。

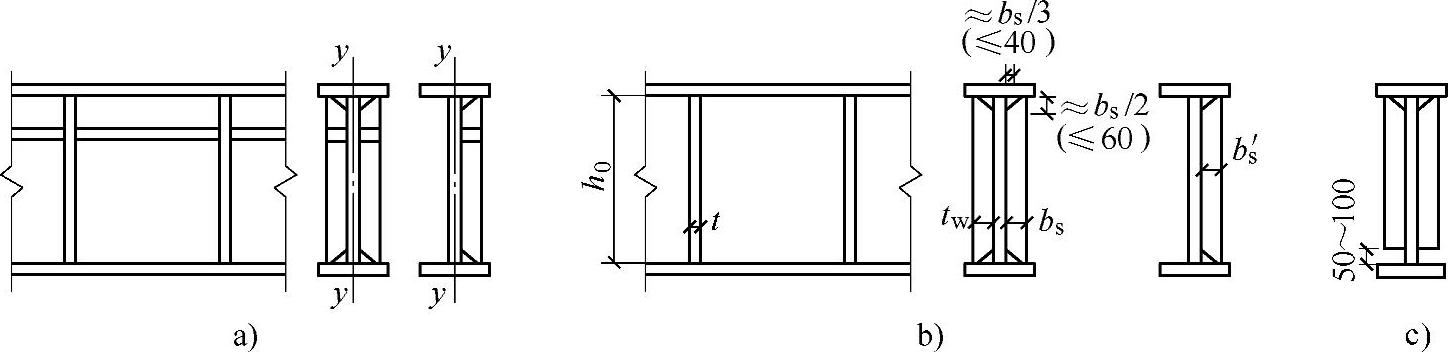
图4-14 加劲肋构造

a）同时用横向加劲肋和纵向加劲肋加强的腹板 b）横向加劲肋的端部切去的斜角 c）50～100mm的断处

4）为使横向加劲肋充分发挥作用和满足施焊的要求，横向加劲肋的间距a应满足式（4-39）。

0.5h₀≤a≤2h₀ （4-39）

5）为了减少焊接应力，避免焊缝的过分集中，横向加劲肋的端部应切去宽约b_s/3（但不大于40mm）高约b_s/2（但不大于60mm）的斜角，如图4-14b所示，以使梁的翼缘焊缝连续通过。在纵向加劲肋与横向加劲肋相交处，应将纵向加劲肋两端切去相应的斜角，使横向加劲肋与腹板连接的焊缝连续通过。

6）对直接承受动力荷载的梁（如吊车梁），为改善梁的抗疲劳性能，不降低疲劳强度，横向加劲肋的下端不应和受拉翼缘焊接，一般在距受拉翼缘50～100mm处断开，如图4-14c所示。

（4）支撑加劲肋的计算 支撑加劲肋是指承受固定集中荷载或者支座反力的横向加劲肋。这种加劲肋必须在腹板两侧成对设置，并进行整体稳定和端面承压计算，其截面往往比中间横向加劲肋大，如图4-15所示。

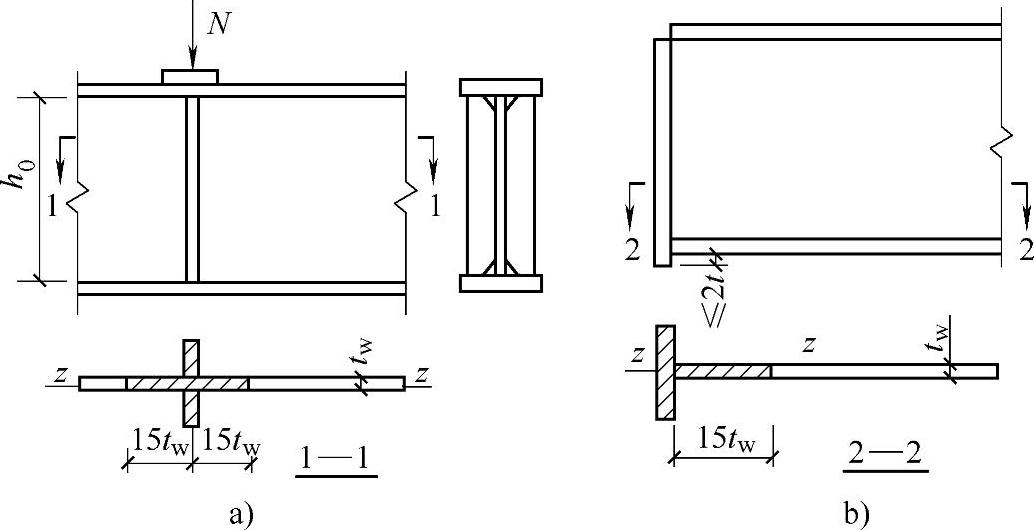
图4-15 支撑加劲肋

a）支撑加劲肋截面 b）突缘支座

1）按轴心受压构件计算支撑加劲肋在腹板平面外的稳定性。此受压构件的截面面积A包括加劲肋和加劲肋每侧15t_w范围内的腹板面积，图4-15中的阴影部分计算长度近似地取为h₀。计算公式为

式中 A——图4-15所示阴影部分的面积；

φ_z——绕z轴失稳的稳定系数。

2）当支撑加劲肋端部刨平顶紧时，应按所承受的固定集中荷载或支座反力计算。其端面承压应力为

σ=N/A_b≤f_ce （4-41）

式中 f_ce——钢材端面承压的强度设计值；

A_b——支撑加劲肋与翼缘板或柱顶相接触的面积。

对于图4-15b所示的突缘支座，若应用式（4-41）按端面承压验算，必须保证支撑加劲肋向下的伸出长度不大于2t。

【例4-3】 有一梁的受力如图4-16a所示（设计值），钢材为Q235，梁截面尺寸和加劲肋布置如图4-16d、e所示，在离支座1.6m处梁翼缘的宽度改变一次（300mm变为150mm）。试验算离支座处第一区格①稳定。

【解】 （1）梁内力的计算 经计算，梁所受的剪力V和弯矩M如图4-16b、c所示。

（2）梁腹板局部稳定的计算 由于没有局部压应力，验算条件为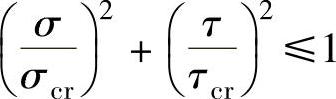

1）支座附近截面的惯性矩：

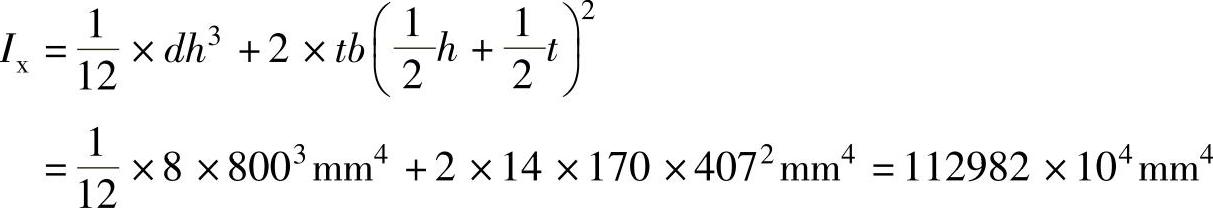
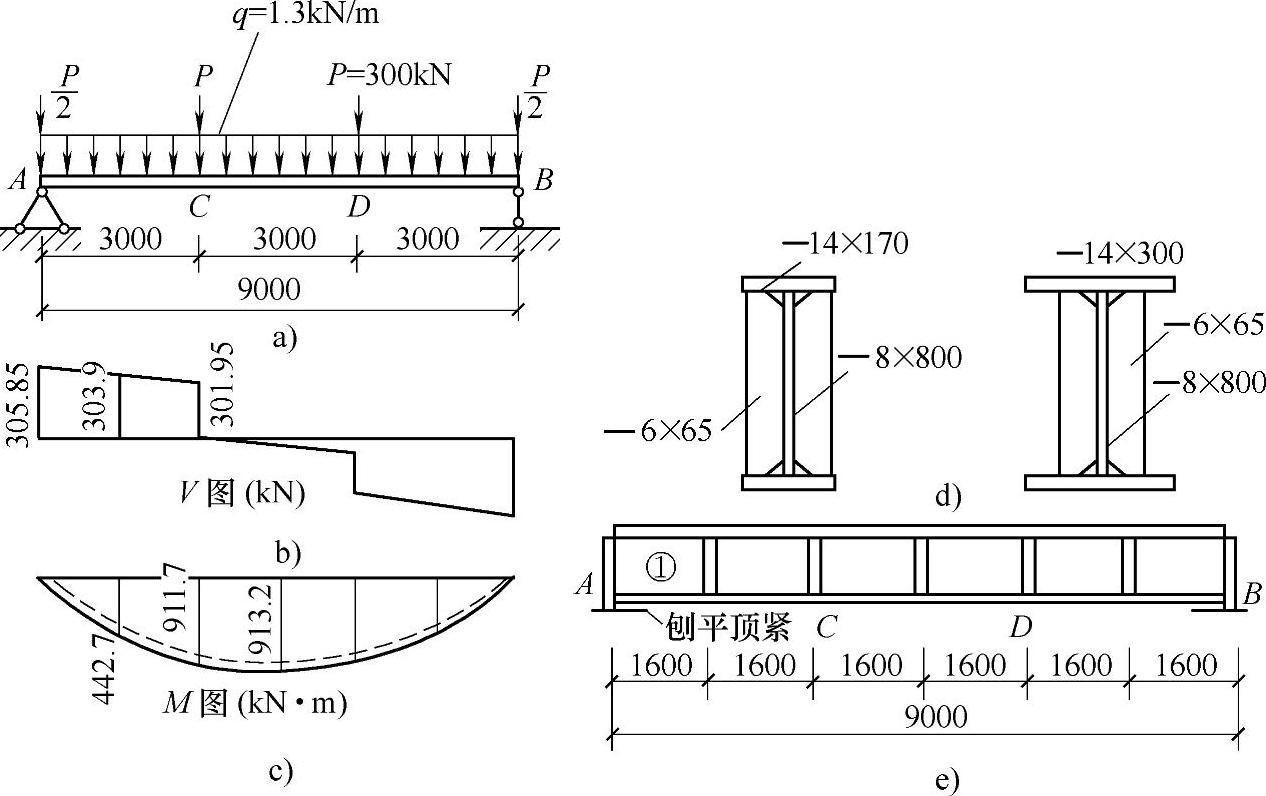
图4-16 验算梁的局部稳定（例4-3）

a）梁的受力 b）梁所受的剪力 c）梁所受的弯矩 d）梁的截面尺寸 e）加劲肋的布置

2）区格两边的弯矩：M₁=0

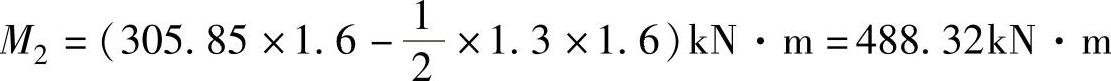
弯矩平均值：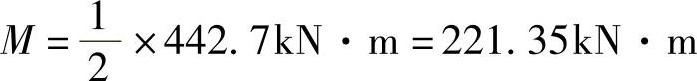

3）区格两边的剪力：V₁=305.85kN·m

V₂=305.85-1.3×1.6kN=303.77kN

剪力平均值：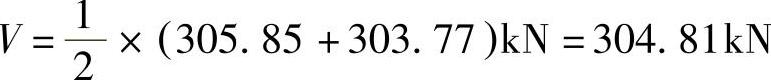

4）

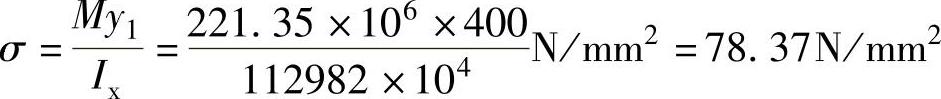
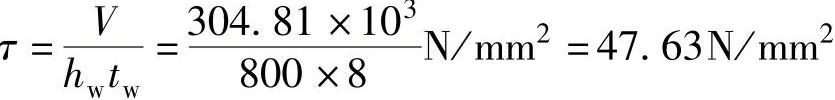
5）假定梁受压翼缘扭转受到约束，则按式，得

所以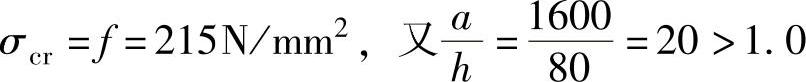

根据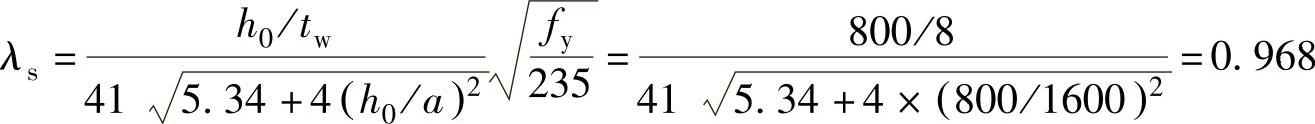

0.8＜0.968＜1.2

则有τ_cr=[1-0.59（λ_s-0.8）]f_v=[1-0.59×（0.968-0.8）]×125N/mm²=112.61N/mm²

6）验算腹板局部稳定：

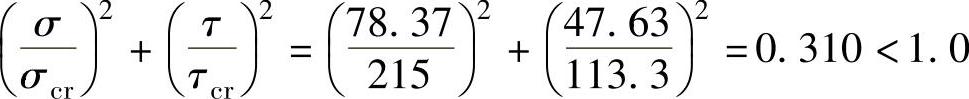
因此，区格①局部稳定条件满足。