1）符合以下情况之一时，可不计算梁的整体稳定：

①有铺板（各种钢筋混凝土板和钢板）密铺在受弯构件的受压翼缘上并与其牢固相连，能够阻止受压翼缘的侧向位移时。

②H型钢或等截面工字形简支梁受压翼缘的自由长度l₁同其宽度b₁之比不超过表4-3中所规定的数值时。

表4-3 H型钢或工字形截面简支梁不需计算整体稳定时l₁/b₁的最大值

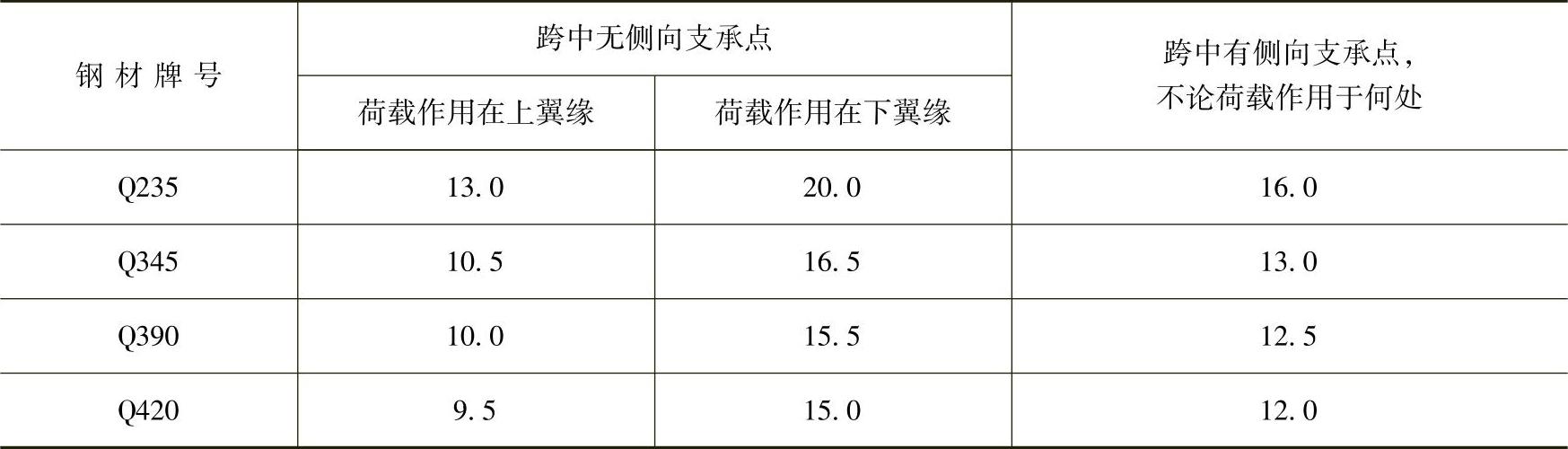
③两端简支的箱形截面受弯构件，其截面高度h与两腹板的间距b₀（图4-9）之间的比h/b₀≤6，并且l₁/b₀≤95（235/f_y）时。

2）受压翼缘的自由长度l₁应按以下规定采用：

①跨中无侧向支撑点时，l₁为受压构件的跨度；

②跨中有侧向支撑点时，l₁为受压翼缘侧向支撑点的距离。

3）在支座处采取构造措施施以避免端部截面发生扭转。

4）当选用表4-3以外钢的牌号时，不需计算整体稳定的l₁/b₁或l₁/b₀最大值应按照Q235钢的数值乘以。

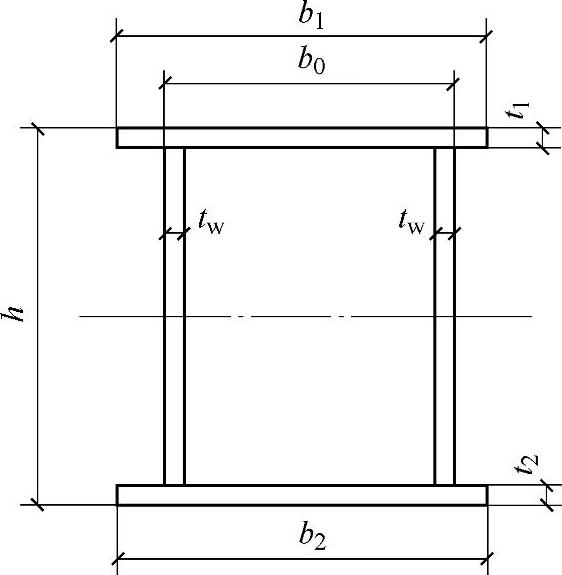
图4-9 箱形截面

5）不能符合第1）条的要求时，应按照表4-4所列公式计算整体稳定。

表4-4 受弯构件整体稳定计算公式

注：M_x、M_y——绕强轴和弱轴作用的最大弯矩；

W_x、W_y——按受压边缘纤维确定的对强轴和弱轴毛截面模量；

γ_y——截面塑性发展系数，按表4-1中的规定采用；

φ_b——绕强轴弯曲所确定的整体稳定系数，按表4-5的规定。

6）整体稳定系数φ_b应按表4-5所列公式计算

表4-5 受弯构件的整体稳定系数φb

注：β_b——受弯构件整体稳定的等效弯矩系数，两端简支时，按表4-6采用；悬臂梁时，按表4-7采用；

λ_y——梁在侧向支承点间对截面弱轴y-y的长细比；

l₁——简支梁时按表4-3的规定采用，悬臂梁时为悬伸长度；

A——受弯构件的毛截面面积；

h、t_l——截面的全高和受压翼缘厚度；

η_b——截面不对称影响系数，对双轴对称工字形截面（图4-10a），η_b=0；对单轴对称工字形截面（图4-10b、

c）。加强受压翼缘时，η_b=0.8（2a_b-1）；加强受拉翼缘时，η_b=2a_b-1。a_b的计算式为

I₁、I₂——受压翼缘和受拉翼缘对y轴的惯性矩；

b、t——槽钢截面的翼缘宽度和厚度。

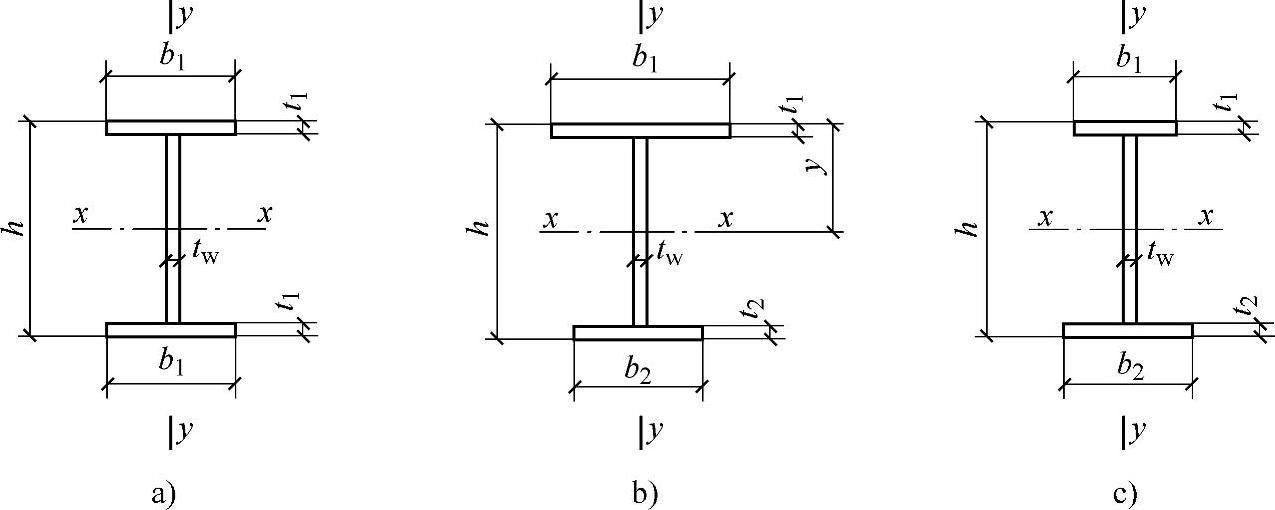
图4-10 焊接工字形（含轧制H型钢）截面

a）双轴对称 b）加强受压翼缘 c）加强受拉翼缘(www.daowen.com)

表4-6 H型钢和等截面工字形简支梁的系数βb

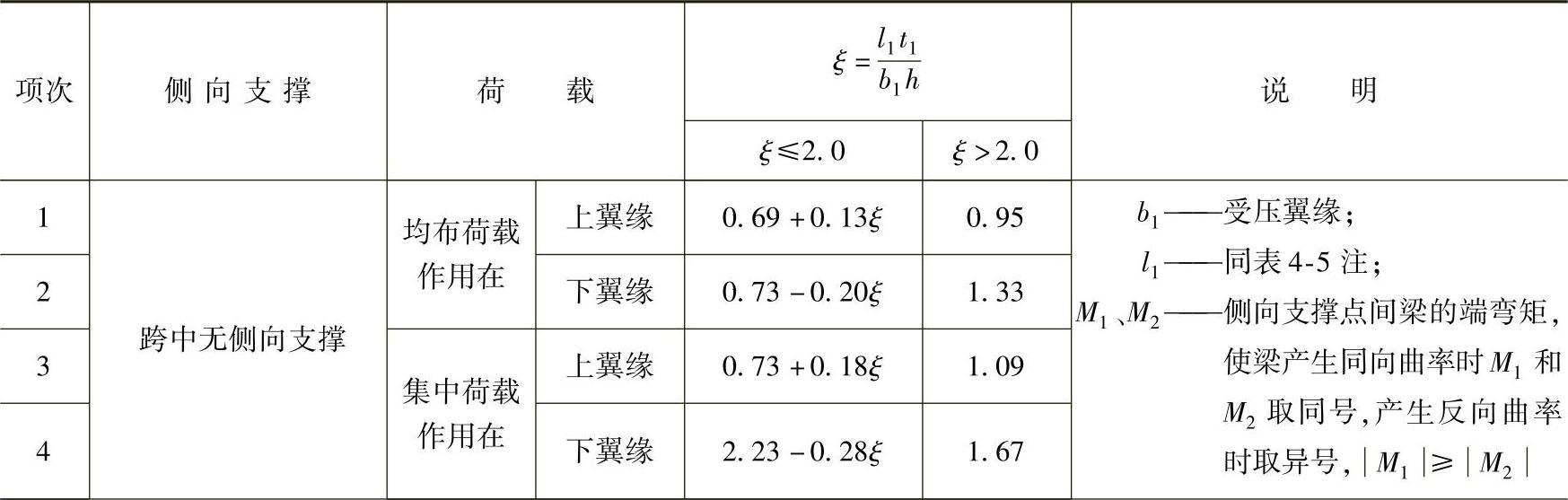
（续）

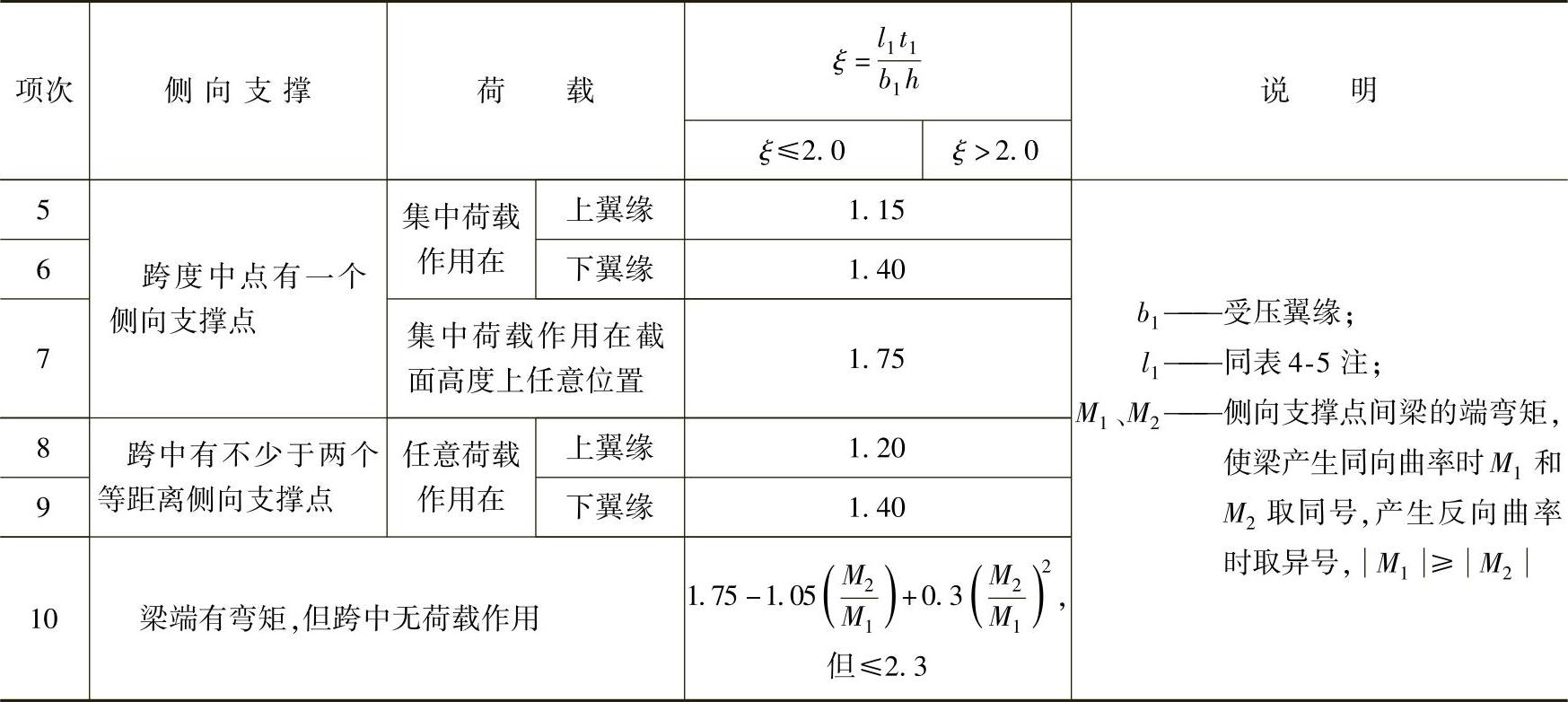
注：1.表中项次3、4和7的集中荷载是指一个或少数几个集中荷载位于跨度中央附近的情况，对其他情况的集中荷载应按项次1、2、5和6内的数值采用。

2.表中项次8、9的β_b，当集中荷载作用在侧向支撑点处时，取β_b=1.20。

3.荷载作用在上翼缘系指荷载作用点在翼缘表面，方向指向截面形心；荷载作用在下翼缘系指荷载作用点在翼缘表面，方向背向截面形心。

4.对α_b＞0.8的加强受压翼缘工字形截面，下列情况的β_b的值应乘以相应的系数。

项次1：当ξ≤1.0时，0.95。

项次2：当ξ≤0.5时，0.90；当0.5＜ξ≤0.5时，0.95。

表4-7 双轴对称工字形等截面（含H型钢）悬臂梁的系数βb

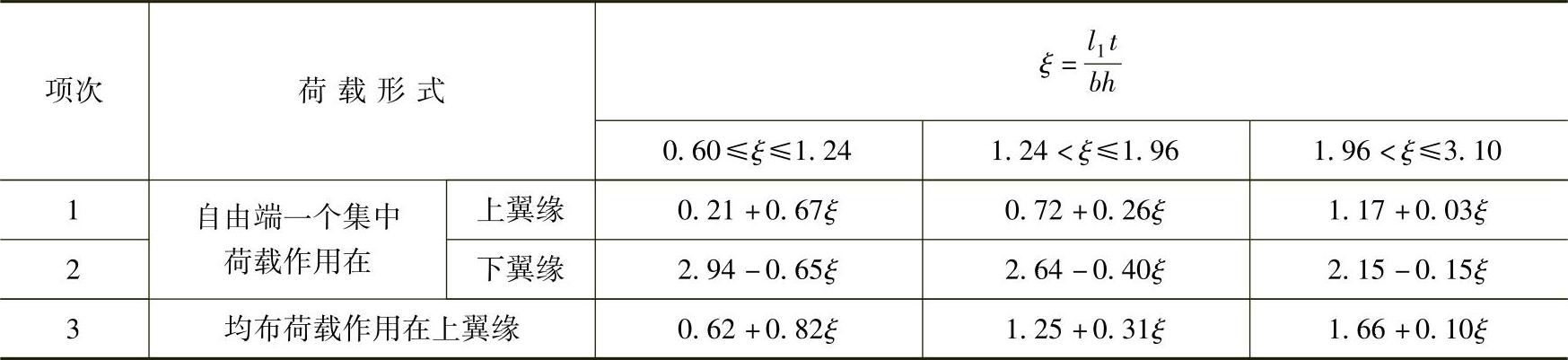
注：1.l₁为悬臂梁的悬伸长度，式（4-16）中λ_y=l₁/i_y。

2.当用于由邻跨延伸出来的伸臂梁时，应在构造上采取措施加强支撑处的抗扭能力。

表4-8 轧制普通工字钢简支梁的φb

（续）

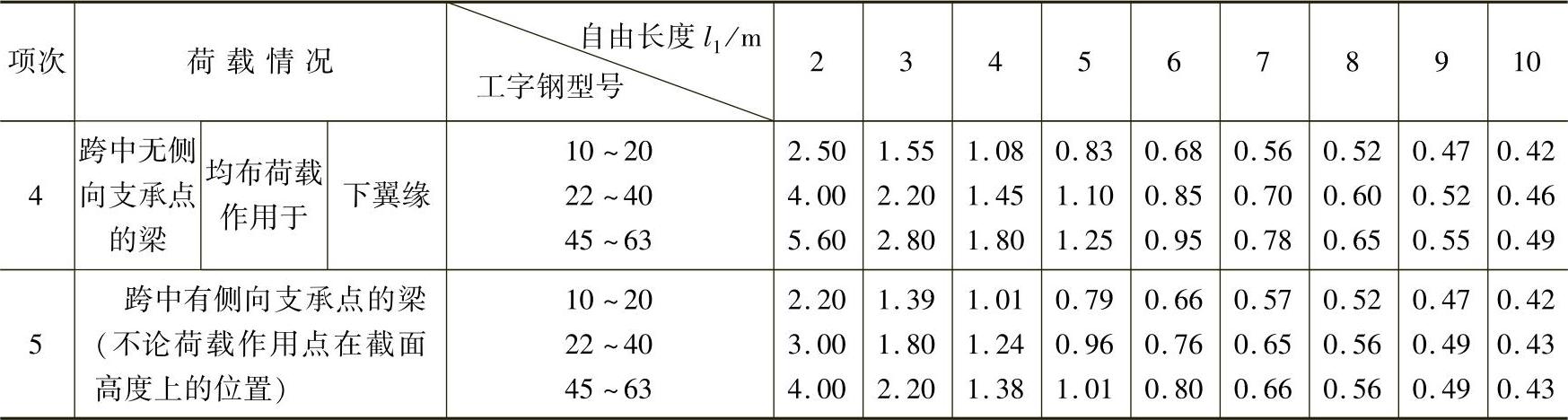
注：1.与表4-6的注1、注3相同。

2.表中的φ_b适用于Q235钢，对其他钢。表中数值应乘以235/f_v。

3.表中φ_b大于0.60时，应按表4-9中的φ_b′代替。

表4-9 整体稳定系数φ′_b

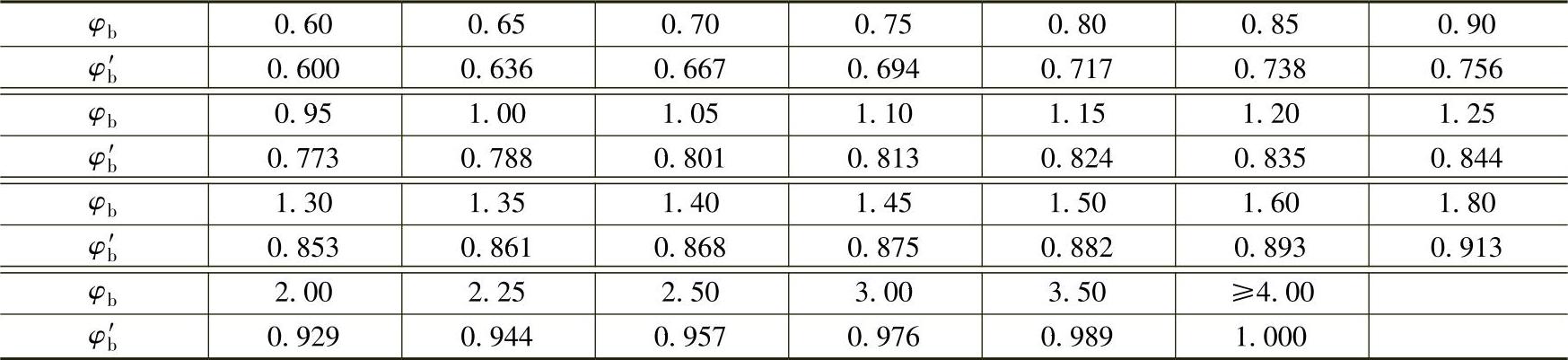
注：φ′_b的计算式为

7）受均布弯矩的受弯构件，当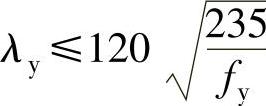时，其整体稳定系数φ_b可按照表4-10中所列的近似公式进行计算。当算得的φ_b值大于0.6时，不需按表4-9换算成φ′_b值，当φ_b＞1时，取φ_b=1。

表4-10 受弯构件整体稳定系数φ_b的近似计算公式

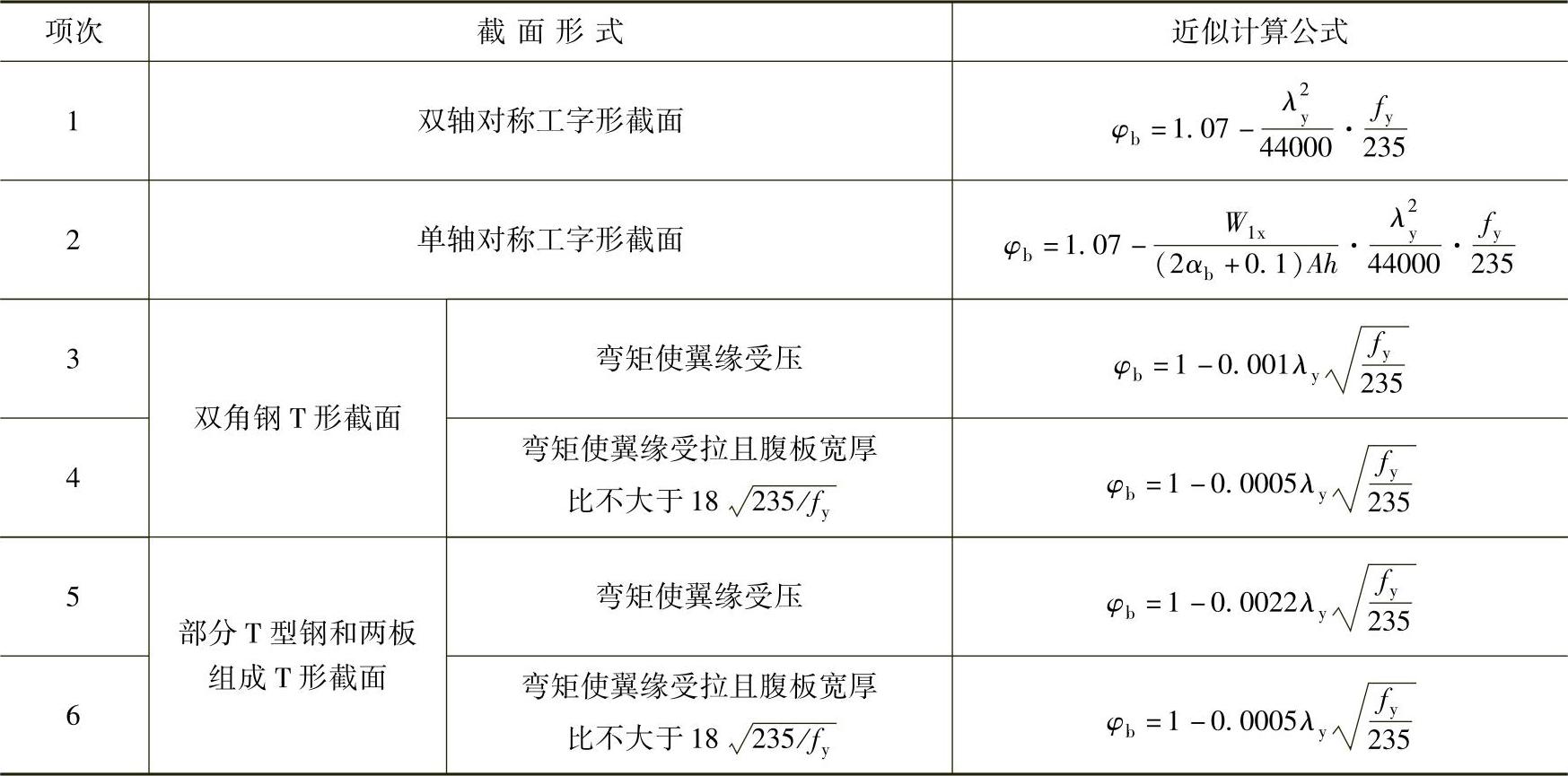
【例4-2】 某轧制普通工字钢简支梁，型号50a，W_x=1860cm，跨度7m，钢材为Q235。梁上翼缘作用均布永久荷载g_k=8kN/m（标准值，含自重）和可变荷载q_k=12kN/m（标准值），并且跨中无侧向支承。试验算此梁的整体稳定性。

【解】 （1）求最大弯矩设计值

（2）求整体稳定系数 按照跨中无侧向支承，均布荷载作用于上翼缘，l₁=7m，查《钢结构设计规范》（GB 50017—2003）附表B.2，得φ_b=0.50＜0.6。

（3）验算整体稳定性 查表1-2得钢材的强度设计值，f=215N/mm2

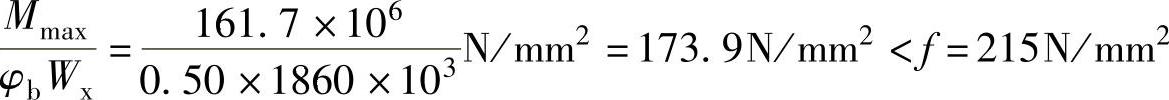
可见，整体稳定性符合要求。