1.梁的抗弯强度
(1)梁截面弯曲正应力的发展阶段 梁截面受弯矩Mx作用时,其上、下边缘正应力σ最大。截面弯矩从零逐渐增加时,截面上的正应力发展可分为三个阶段,即弹性阶段、弹塑性阶段以及塑性阶段。
1)弹性阶段。当作用在梁上的弯矩Mx较小时,其截面边缘应力σ<fy,全截面材料为弹性,应力与应变成正比关系,而此时截面上应力成直线分布。弹性阶段的极限情况如图4-4b所示,此时的弯矩承载力为
Mxe=fyWnx (4-2)
式中 Wnx——梁的净截面对中和轴x的截面模量。
2)弹塑性阶段。当弯矩Mx继续增加,截面边缘应变ε>fy/E时,截面边缘材料已经屈服,其截面出现了塑性区,此区高度为a(0<a<h/2)。因为此范围的钢材已经屈服,所以此区域上的正应力均等于fy,而此时中间截面部分材料仍保持为弹性,应力与应变成正比,如图4-4c所示。
3)塑性阶段。当弯矩Mx继续增加,梁截面的塑性区不断向内发展,到最后全截面达到塑性,弹性区域完全消失,如图4-4d所示。此时,梁的抗弯承载能力达到极限。此后Mx将不再继续增加,但变形继续增加,形成“塑性铰”。塑性工作阶段的最大弯矩为
Mxp=fy(S1nx+S2nx)=fyWpnx (4-3)
式中 S1nx、S2nx——中和轴以上、以下净截面对中和轴x的面积矩;
Wpnx——净截面对x轴的塑性模量,Wpnx=(S1nx+S2nx)。
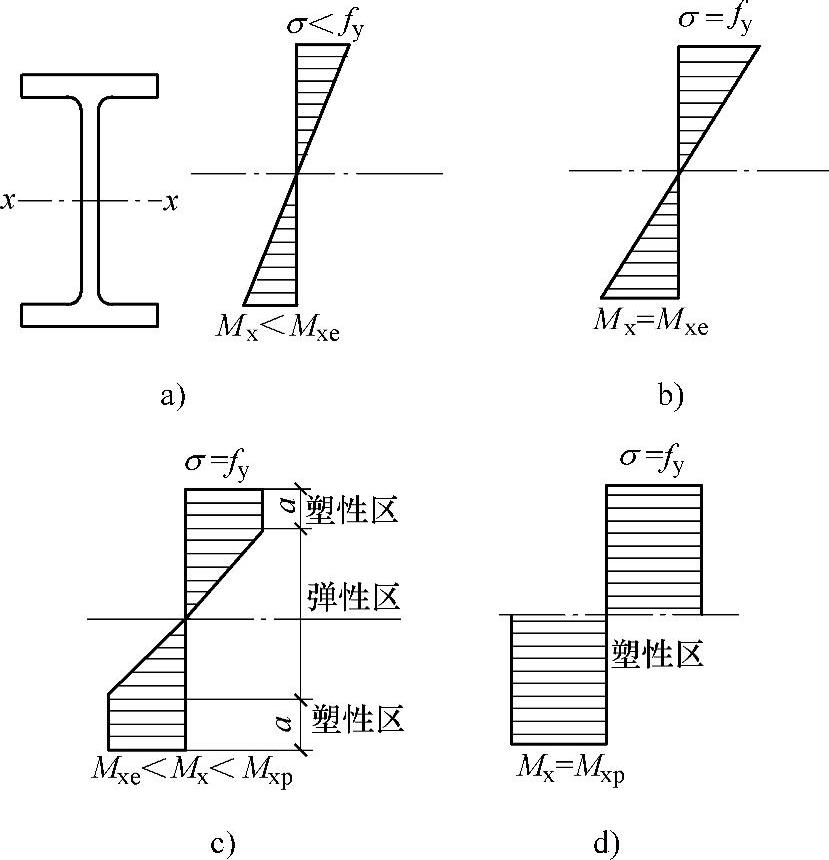
图4-4 梁受弯时各阶段的截面正应力分布
(2)截面形状系数γF 塑性阶段的最大弯矩Mxp与弹性阶段的最大弯矩Mxe之间的比即为截面形状系数,用γF表示,即

γF值的大小反映了截面可利用塑性的程度,其值取决于截面的几何形状,并且同材料的性质无关。一些截面的γF值如图4-5所示。
2.梁的弯曲正应力强度计算公式
钢梁受弯时,其正应力-应变曲线相似于其受拉时,屈服点也相差不多。所以,梁的抗弯强度计算仍然采用钢材为理想弹-塑性体的假定。
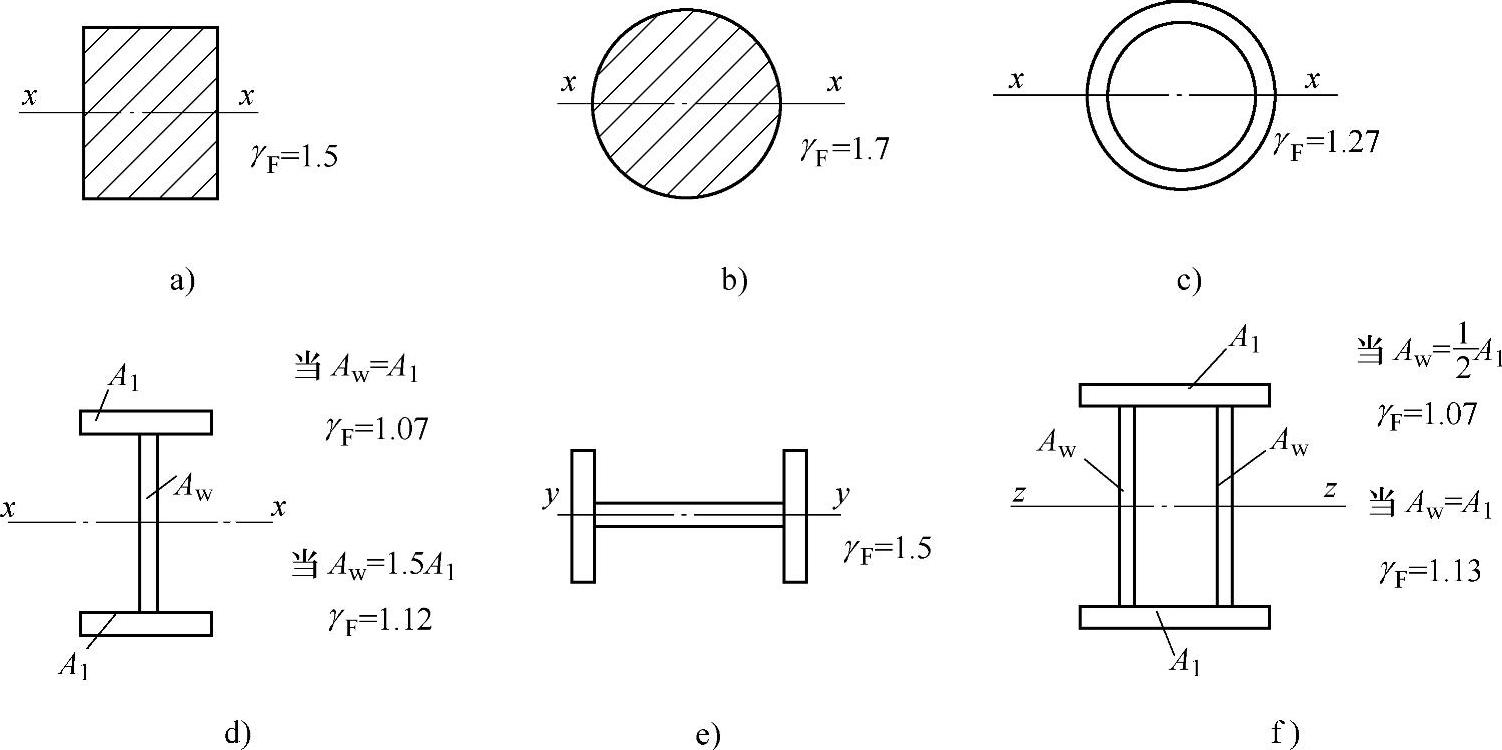
图4-5 截面形状系数
a)矩形截面 b)圆形截面 c)环形截面 d)带翼缘截面 e)工字形截面 f)箱形截面
在截面上、下边缘应力达到屈服点fy之前,材料处于弹性阶段,梁截面满足平截面假定(图4-4a)。梁按照弹性设计时,是把截面纤维屈服作为极限状态,其强度条件计算式为

式中 Mx——绕梁截面z轴的弯矩;
f——钢材的抗弯强度设计值;
Wnx——梁截面对z轴的净截面模量;
fy——钢材的屈服强度;
γR——材料抗力分项系数。
计算梁的抗弯强度时,考虑截面塑性发展会节省钢材,但如果按照截面形成塑性铰来设计,可能使梁的挠度过大,受压翼缘会过早的发生局部失稳。所以,梁截面钢材的塑性只能有限度地进行利用,依据《钢结构设计规范》(GB 50017—2003)规定,取塑性发展深度a≤0.125h。梁按塑性方法设计的抗弯强度计算公式为式(4-6)、式(4-7)。
受单向弯矩(Mx)作用的梁:

受双向弯矩(Mx、My)联合作用的梁:

式中 Mx、My——绕x轴和y轴的弯矩;
f——钢材的抗弯强度设计值;
Wnx、Wny——截面对x轴和y轴的净截面模量;
γx、γy——截面对x轴和y轴的塑性发展系数,各种截面塑性发展系数的取值见表4-1。
表4-1 截面塑性发展系数γx、γy
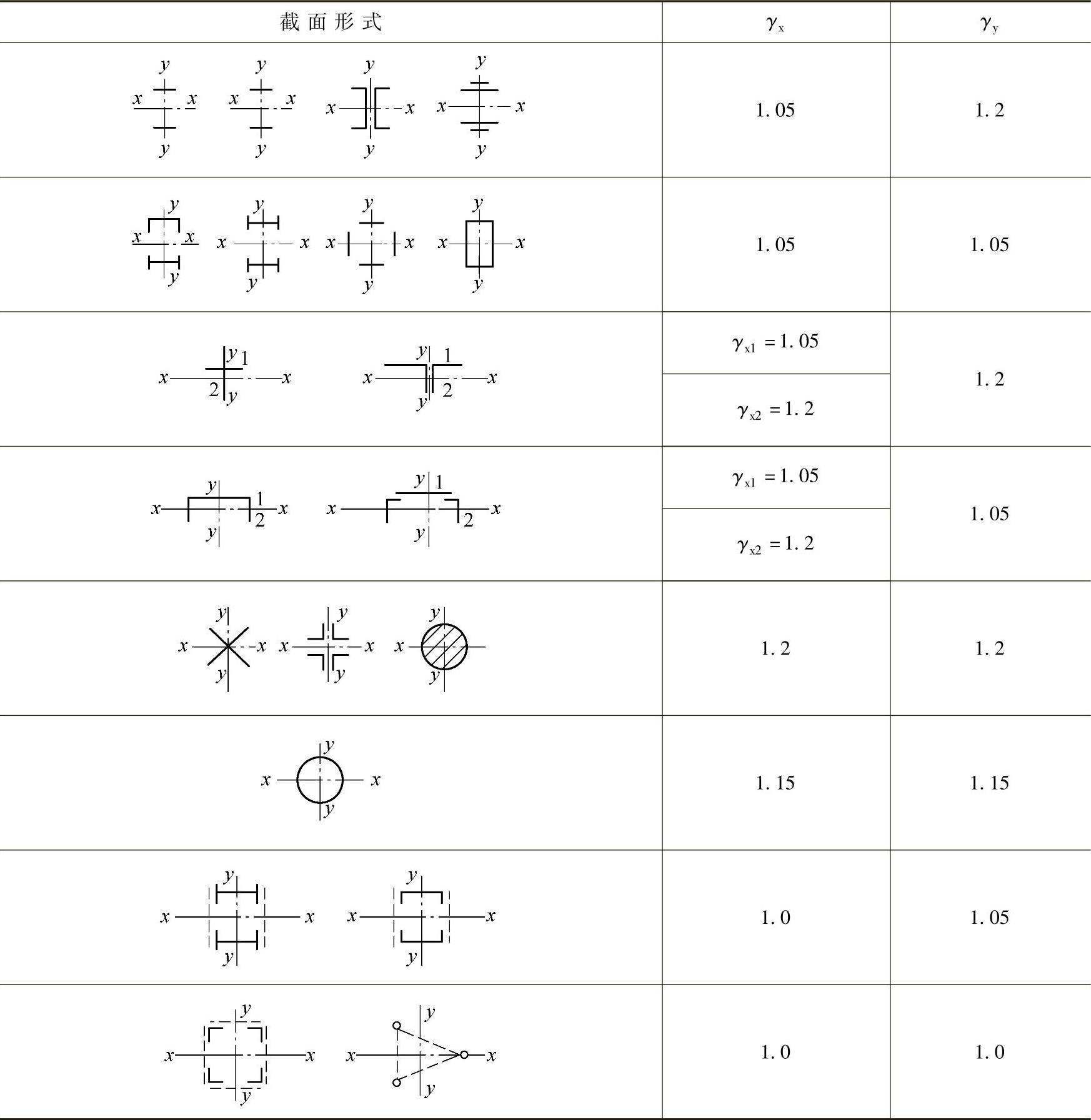
截面塑性发展系数γx与γy的选用应注意下列几方面。
1)为防止梁在失去强度之前受压翼缘局部失稳,《钢结构设计规范》(GB50017—2003)规定:宽厚比满足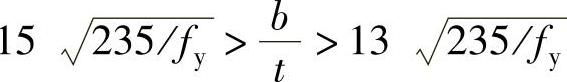 时,应取γx=1.00。b、t分别为梁受压翼缘的自由外伸宽度及厚度;fy为钢材屈服点(不分钢材厚度)。
时,应取γx=1.00。b、t分别为梁受压翼缘的自由外伸宽度及厚度;fy为钢材屈服点(不分钢材厚度)。
2)直接承受动力荷载且需要进行计算疲劳强度的梁,如重级工作制吊车梁,塑性深入截面将使钢材发生硬化,致使疲劳断裂提前出现,应取γx=γy=1.0。
3.梁的抗剪强度
一般情况下,梁既承受弯矩,又承受剪力。工字形和槽形截面梁腹板上的剪应力分布如图4-6所示。
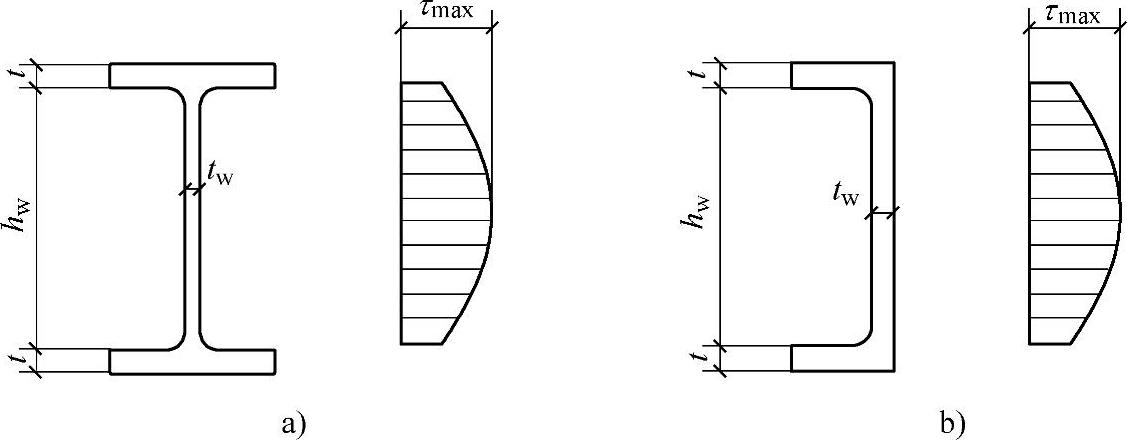
图4-6 腹板剪应力
a)工字形截面梁腹板剪力分布 b)槽形截面梁腹板剪力分布
梁在主平面内受弯时,其横截面上任一点处的剪应力计算式为

式中 V——计算截面沿腹板平面作用的剪力;
S——计算剪应力处以上毛截面对中和轴的面积矩;
I——毛截面惯性矩;
tw——腹板厚度。(https://www.daowen.com)
梁截面上最大剪应力发生在腹板中和轴处,所以抗剪强度计算式为

式中 Smax——中和轴以上毛截面对中和轴的面积矩;
fv——钢材的抗剪强度设计值。
当梁的抗剪强度不足时,最有效的办法是增大腹板的厚度tw。
4.梁的局部承压强度
当梁的翼缘受有沿腹板平面作用的集中荷载,并且该荷载处又未设置支承加劲肋,通常认为集中荷载从作用处以45°角扩散,均匀分布于腹板边缘局部范围之内(图4-7),腹板计算高度上边缘局部承压强度计算式为

式中 F——集中荷载,对动力荷载应考虑动力系数;
ψ——集中荷载增大系数,对重级工作制吊车梁,ψ=1.35;对其他梁ψ=1.0;
lz——集中荷载在腹板计算高度上边缘的假定分布长度,计算式为
lz=a+5hy+2hR (4-11)
a——集中荷载沿梁跨度方向的支承长度,对吊车梁可取为50mm;
hy——自梁顶面至腹板计算高度h0上边缘的距离;
hR——轨道的高度,对梁顶无轨道的梁hR=0;
h0——腹板的计算高度,对轧制型钢梁为腹板与上、下翼缘相接处两内弧起点间的距离;对焊接组合梁为腹板高度;对铆接或高强度螺栓连接组合梁,为上、下翼缘与腹板连接的铆钉或高强度螺栓线间最近距离。
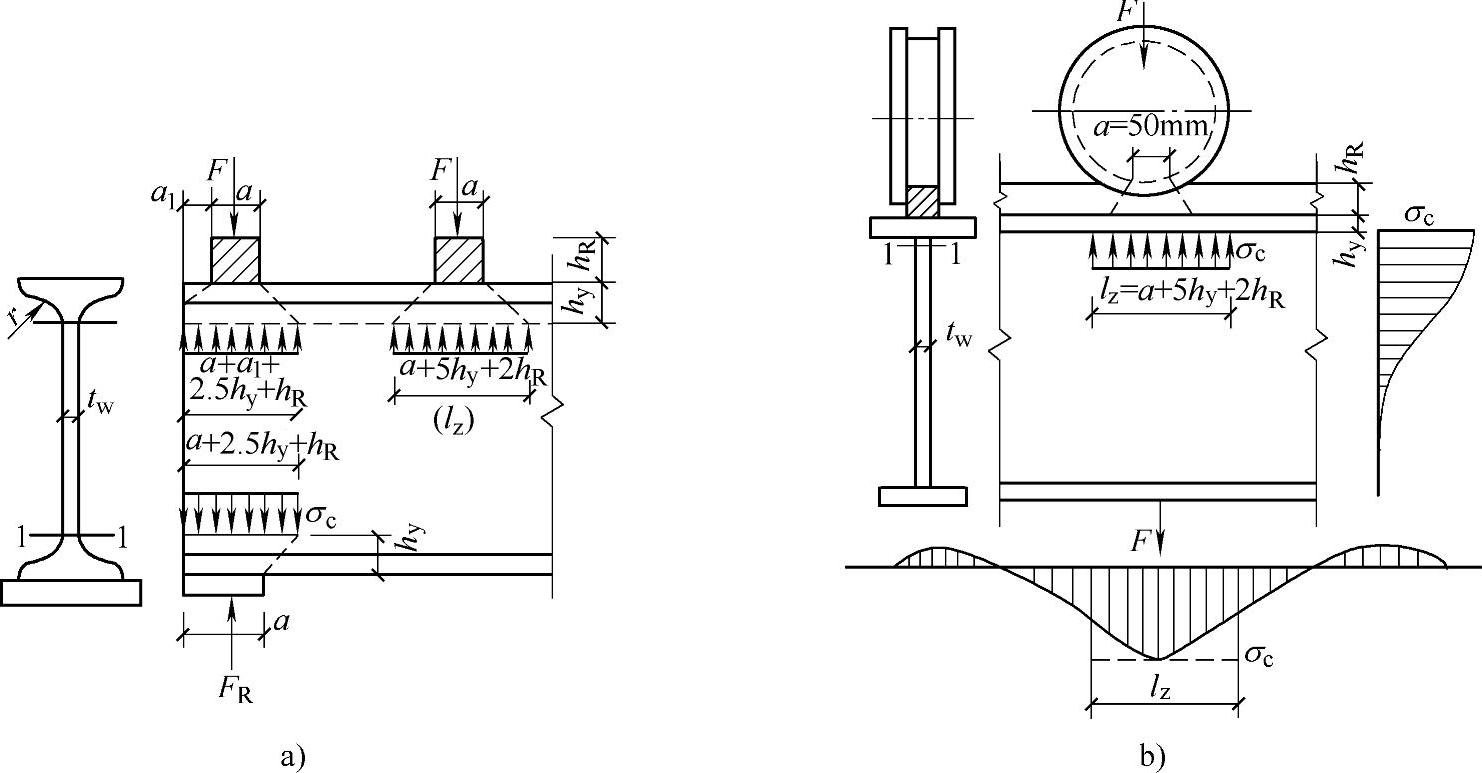
图4-7 局部承压腹板边缘压应力分布
a)固定集中荷载作用在无支承加劲肋处 b)移动集中荷载作用在无支承加劲肋处
在梁的支座处,当不设置支承加劲肋时,也应按上式计算腹板计算高度下边缘的局部承压强度,但取ψ=1.0;支座反力的假定分布长度应根据支座具体尺寸,可按式(4-11)计算。
5.折算应力计算
在组合梁的腹板计算高度边缘处,如果同时受有较大的正应力、剪应力以及局部压应力,或同时受有较大的正应力和剪应力,如连续梁支座处或梁的翼缘截面改变处,其折算应力计算式为
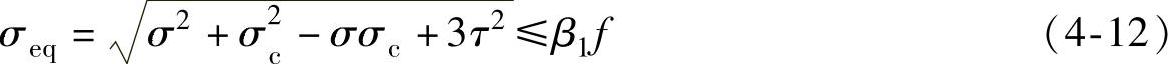
式中 σ、τ、σc——腹板计算高度边缘同一点上同时产生的正应力、剪应力和局部压应力,τ和σc应按式(4-8)和式(4-10)计算,σ应按式(4-13)计算:

σ和σc以拉应力为正值,压应力为负值;
In——梁净截面惯性矩;
y1——计算点至梁中和轴的距离;
β1——计算折算应力的强度设计值增大系数,考虑到计算折算应力的最大值仅发生在梁的局部范围,对梁的不利影响不大,故采用提高钢材强度设计值的办法予以考虑。当σ与σc异号时,取β1=1.2;当σ与σc同号或σc=0时,取β1=1.1。
在主平面内受弯的实腹梁,其抗剪强度计算式为

式中 Fv——计算截面沿腹板平面作用的剪力;
S——计算剪应力处以上毛截面对中和轴的面积矩;
I——毛截面惯性矩;
tw——腹板厚度
fv——钢材抗剪强度设计值。
型钢梁因腹板较厚,一般均能满足抗剪强度要求,若最大剪力处截面无削弱,则可不必进行计算。
【例4-1】 如图4-8所示的热轧钢普通工字钢简支梁,梁上翼缘作用有均布荷载设计值q=35kN/mm(包括自重),该梁为支撑于主梁顶上的次梁,未设置加劲肋,跨中无侧向支承,支承长度a=100mm,荷载标准值qk=27.69N/mm,梁的型号为 36a,材料为Q235B,跨度为6m。Wx=875cm3,Ix=15800cm4,tw=10mm,hy=t+r,此处:t=15.8mm,r=12mm,f=215N/mm2。试试验算此梁的强度。
36a,材料为Q235B,跨度为6m。Wx=875cm3,Ix=15800cm4,tw=10mm,hy=t+r,此处:t=15.8mm,r=12mm,f=215N/mm2。试试验算此梁的强度。
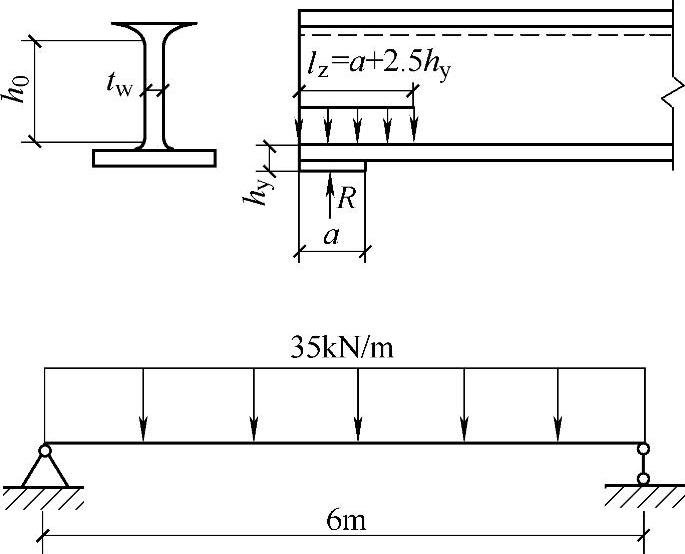
图4-8 带靴梁的柱脚(例4-1)
【解】 (1)最大弯矩设计值
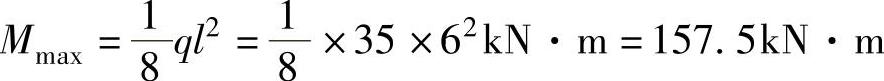
(2)验算强度 根据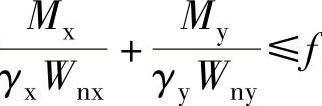 ,由于My=0,得
,由于My=0,得
抗弯强度: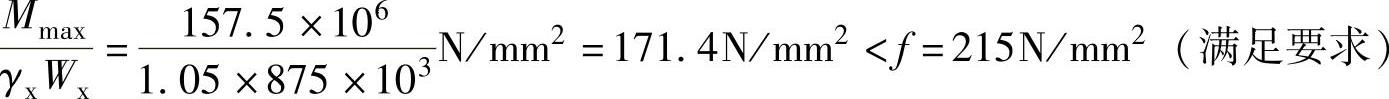
抗剪强度:截面无削弱,型钢可不必计算。
局部承压:翼缘上承受均衡载荷,可不作局部承压验算;梁支承于主梁顶面上,并且端部无支承加劲肋,应验算支座处局部承压强度。
支座反力: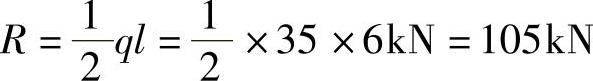
根据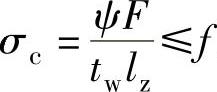 及其规定,得
及其规定,得
hy=r+t=(12.0+15.8)mm=27.8mm
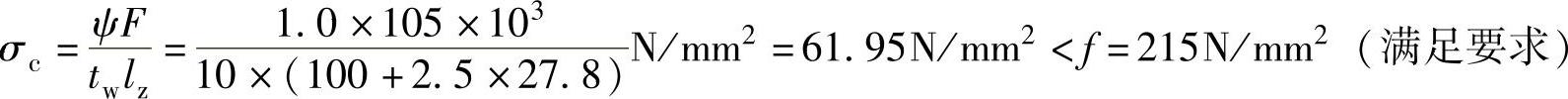
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







