1.组成轴心受压构件的板件的屈曲现象

组成构件的板件，如工字形截面的翼缘和腹板，为得到较大的抗弯刚度，通常其厚度远小于宽度。在均匀压应力的作用下，当压力达到某一数值时，板件就可能产生凸曲现象（图3-16），这就是局部失稳现象。

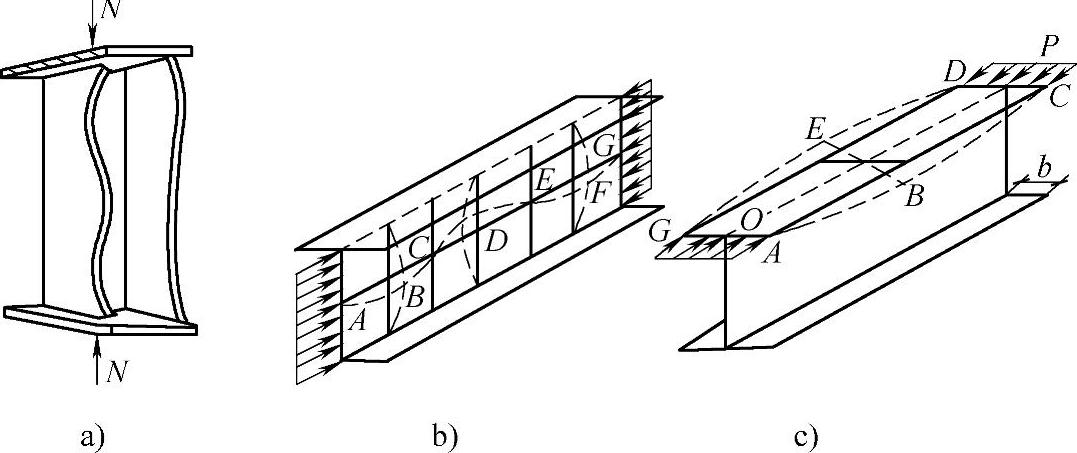
图3-16 轴心受压构件局部屈曲

a）翼缘凸曲现象 b）曲板屈曲变形 c）翼缘屈曲变形

2.四边简支薄板弹性屈曲的临界应力

如图3-17所示的四边简支矩形薄板，在纵向单位宽度均布压力N_x作用下，由薄板的弹性稳定理论可得到其临界应力公式为

式中 K——板的屈曲系数，不同的支撑条件，其值不同；

E、ν——材料的弹性模量、泊松比；

t、b——薄板的厚度和宽度。

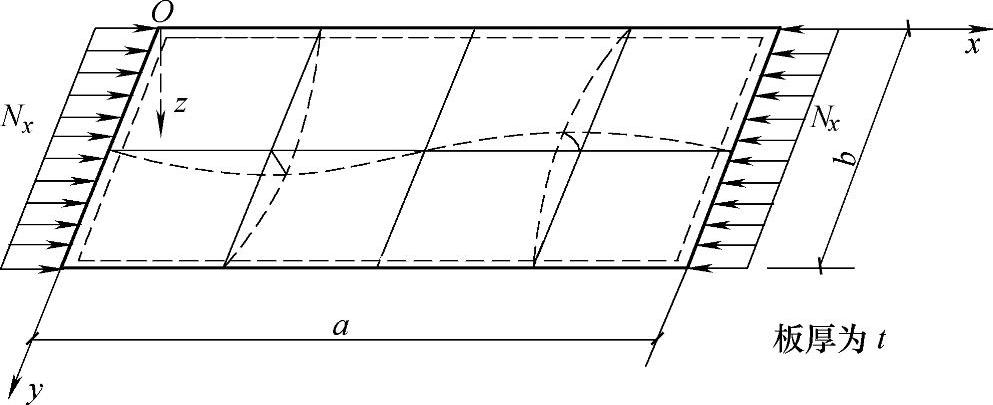
图3-17 四边简支矩形薄板在纵向均布压力作用下的屈曲

由式（3-36）可见，纵向均匀受压的临界应力的大小，取决于宽厚比b/t。

非弹性（弹塑性）任意支撑屈曲的临界应力公式为

式中 χ——不小于1的嵌固系数；

η——弹性模量修正系数，是长细比λ的函数。

3.板件宽（高）厚比的限值

《钢结构设计规范》（GB 50017—2003）对轴心压杆规定，组成压杆的板件的失稳不应先于压杆的整体失稳。

1）翼缘宽厚比的限值。在弹性工作范围内，有

式中 b₁——翼缘的外伸宽度；

t——翼缘板的厚度。

将K=0.425，ν=0.3，λ=75（常用值）代入式（3-38）得(www.daowen.com)

在弹塑性工作阶段，腹板对翼缘没有约束作用，取χ=1。η和φ都是λ的函数，于是得到图3-18中的了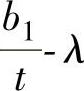曲线（虚线）。规范规定用三段直线代替，如图3-18中实线所示，则有

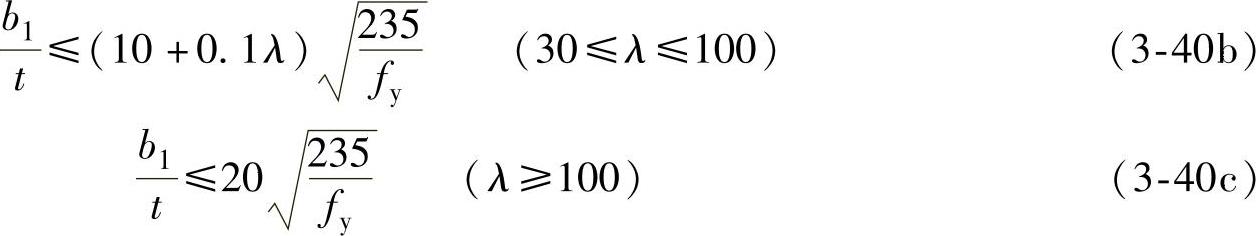
2）腹板高厚比的限制。翼缘对腹板的屈曲有约束作用，χ=1.3，K=4，则

于是得到图3-19中的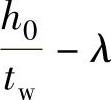

曲线（虚线），规范规定三直线代替曲线，如图3-19中实线所示，则有

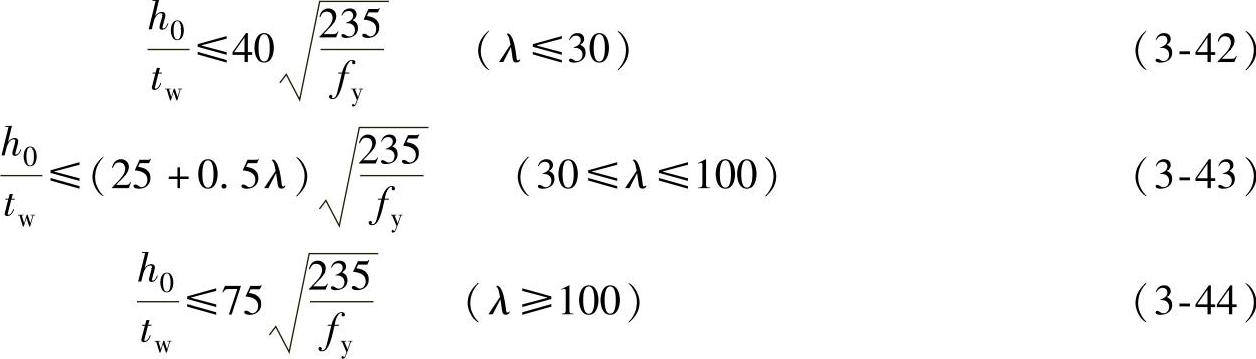
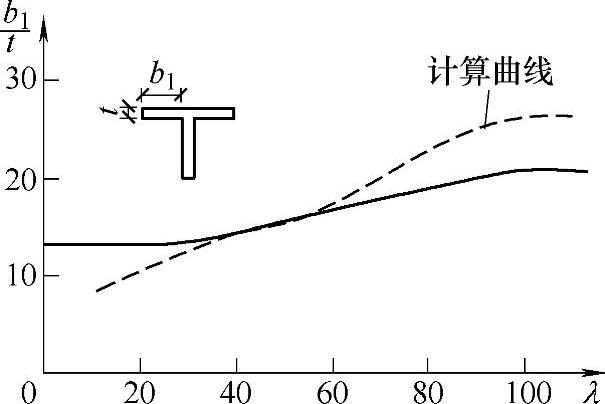
图3-18 工字形截面轴心压杆翼缘的宽厚比

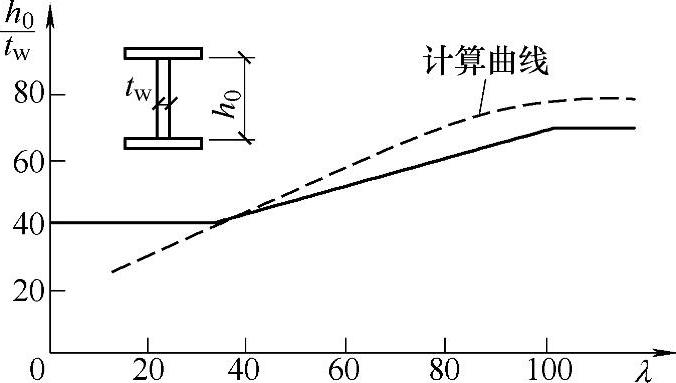
图3-19 工字形截面轴心压杆腹板的宽厚比

双腹壁箱形截面的腹板高厚比偏于安全，取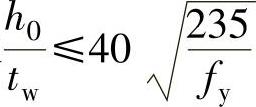

【例3-5】 如图3-20所示，钢材为Q345，翼缘板为焰切边，截面无削弱，焊接组合工字型截面轴心受压柱，柱的计算长度l_0x=6m，l_0y=3m，轴心压力设计值N=2000kN。试验算实腹柱腹板和翼缘的局部稳定。

【解】 腹板高度h₀=250mm，厚度t_w=10mm，长细比λ=50.4，翼缘外伸宽度b=125mm，宽度t=14mm。

腹板局部稳定性：

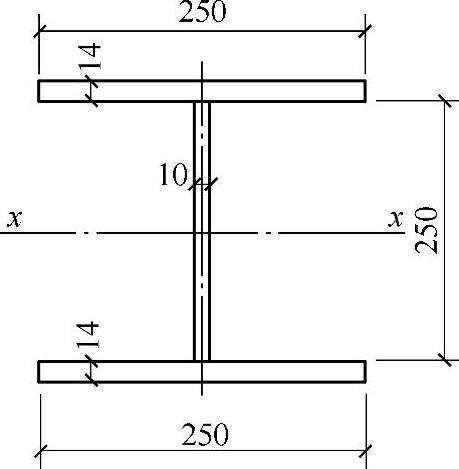
图3-20 工字截面柱（例3-5）

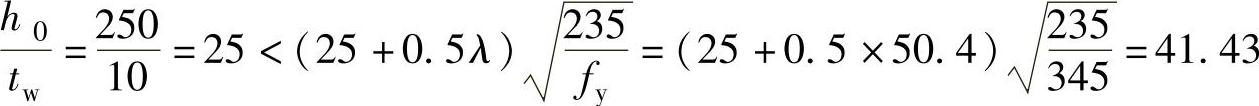
翼缘局部稳定性：

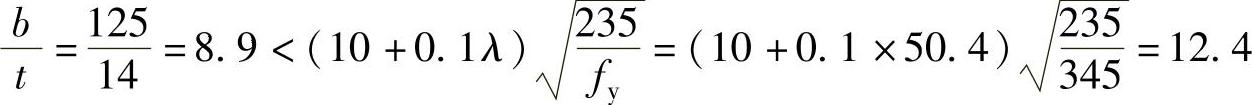
腹板和翼缘的局部稳定性均能得到保证。