1.理想轴心压杆的整体屈曲形式

所谓的理想轴心压杆就是假定杆件完全挺直，荷载沿杆件形心轴作用，杆件在受荷之前既没有初始应力，也没有初弯曲和初偏心等缺陷，截面沿杆件是均匀的。若此种杆件失稳，即称为发生屈曲。屈曲包括以下三种形式。

（1）弯曲屈曲 只发生弯曲变形，杆件的截面只绕一个主轴旋转，杆的纵轴由直线变成曲线，这是双轴对称截面最为常见的一种屈曲形式。图3-13a所示为两端铰接工字形截面压杆发生绕弱轴（y轴）的弯曲屈曲现象。

（2）扭转屈曲 失稳时杆件除支承端外的各截面均绕纵轴扭转，它是某些双轴对称截面压杆可能发生的屈曲形式。图3-13b所示为长度较小的十字形截面杆件可能发生的扭转屈曲情况。

（3）弯扭屈曲 单轴对称截面绕对称轴屈曲时，杆件在发生弯曲变形的同时也会伴随着扭转。图3-13c所示即为T形截面的弯扭屈曲情况。

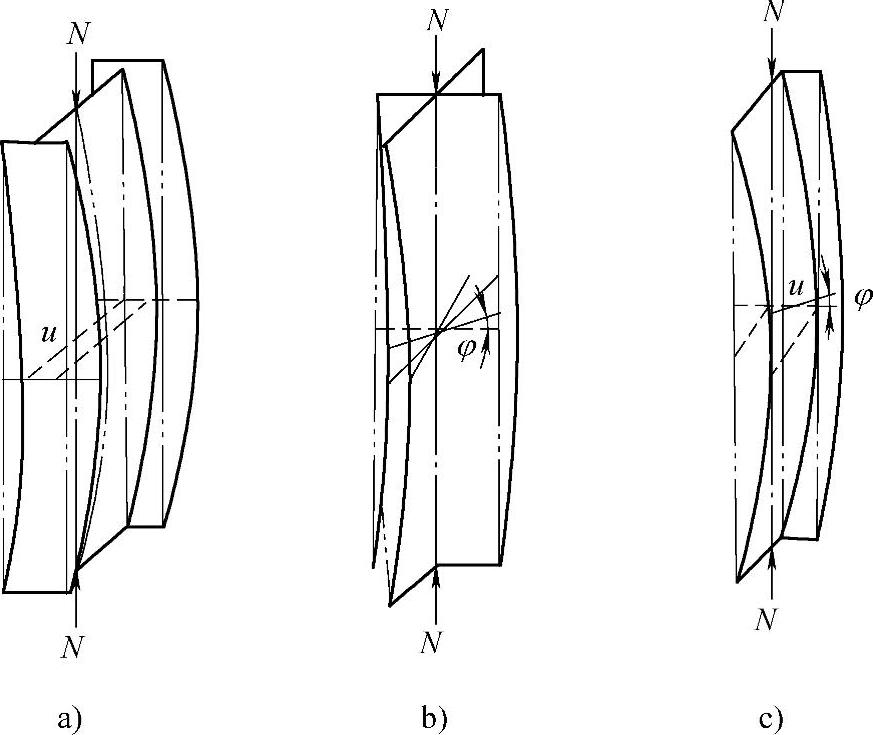
图3-13 轴心压杆的屈曲变形

a）弯曲屈曲 b）扭转屈曲 c）弯扭屈曲

2.理想轴心压杆的整体稳定计算

如图3-14所示的两端铰接的理想细长压杆，若压力N较小，则杆件只有轴心压缩变形，杆轴保持平直。若有干扰使其微弯，则撤去干扰后，杆件即恢复原来的直线状态，这说明荷载对微弯杆各截面的外力矩小于各截面的抵抗力矩，直线状态的平衡是稳定的。当逐渐加大N到某一特定数值时，如遇干扰，杆件就可能发生微弯；此时该干扰撤去后，杆件会保持微弯状态不再恢复其原有的直线状态（图3-14）；这时除直线形式的平衡外，还会存在微弯状态下的平衡位置，这种现象即为平衡的“分枝”；若外力N超过此数值，则微小的干扰将使杆件产生相当大的弯曲变形，杆件随即破坏。中性平衡状态是从稳定平衡向不稳定平衡过渡的一个临界状态，因此称此时的外力N为临界力。这个临界力可定义为理想轴心压杆呈微弯状态的轴心压力。

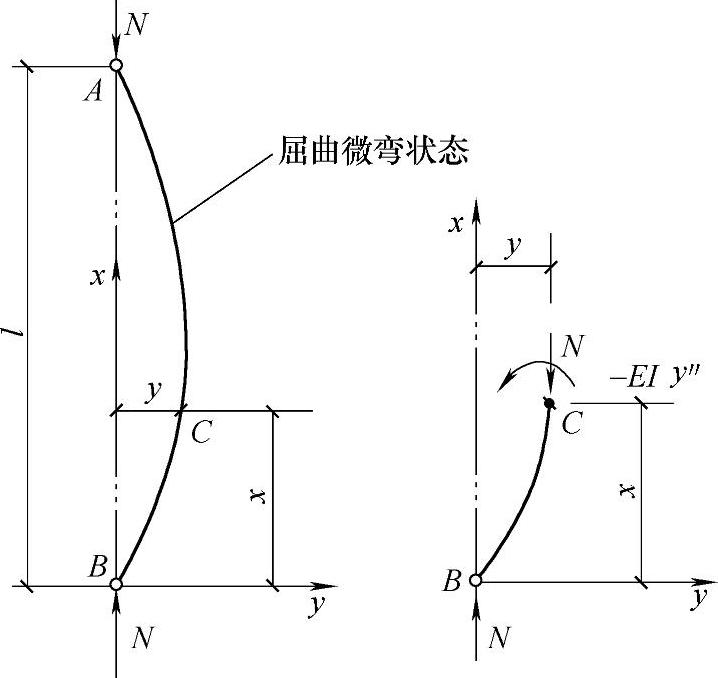
图3-14 两端铰接轴心压杆的临界状态

欧拉（Euler）对理想轴心压杆的整体稳定问题进行了研究，并且得到了著名的欧拉临界力，即

式中 N_E——欧拉临界力；

E——材料的弹性模量；

A——压杆的截面面积；

λ——压杆的长细比；

i——截面的回转半径；

I——截面惯性矩。

若轴心压力N＜N_E，则压杆维持直线平衡状态，不发生弯曲；若N=N_E，则压杆发生弯曲并处于曲线平衡状态。(www.daowen.com)

另外，欧拉临界力只适用于弹性范围。弹塑性阶段发生弯曲屈曲的轴心受压杆件可以采用切线模量理论或者折算模量理论进行解决。

（1）切线模量理论 该理论认为，在非弹性应力状态，应当取应力-应变关系曲线上相应应力点的切线斜率E_t（称为切线模量）来替代线弹性模量E。因此图3-14所示的轴心压杆的非弹性临界力为

（2）折算模量理论 又称双模量理论。该理论认为，荷载达到临界值后杆件就会发生弯曲，这将导致截面上一部分加压，而另一部分减压。此时减压区采用弹性模量E，加压区采用切线模量E_t。于是，图3-14所示的轴心压杆的临界力为

式中 I₁、I₂——截面的减压区和加压区对中性轴的截面惯性矩。

试验结果表明，临界力都达不到N_r，而比较接近于N_t。其原因是失稳的瞬间既有弯曲应力增量又有轴压力增量，整个截面没有卸载区，仍然处于非弹性状态，故应用切线模量来描述。

3.实际轴心受压构件整体稳定计算

（1）轴心受压构件的实际承载力 由压杆的压力挠度曲线可知（图3-15）：理想的直杆轴心受压柱，其弹性屈曲（曲线a，其临界力为欧拉荷载N_E）与弹塑性屈曲（曲线b，其临界荷载为N_crt）均属于分枝型失稳。

实际轴心受压柱的挠度曲线c表示压杆一经压力作用就将产生挠度，A点表示中央截面边缘开始屈服，进入了弹塑性发展阶段；C点则表示达到极值，在C点之前，柱内部抗力与外力之间维持稳定平衡状态；而在C点之后，柱内部抗力与外力之间不能维持稳定平衡，属于极值点失稳。极值点的极限承载力用N_u表示，其数值主要取决于柱长度、初弯曲、柱截面形状和尺寸及残余应力的分布及峰值，用数值积分法来确定。

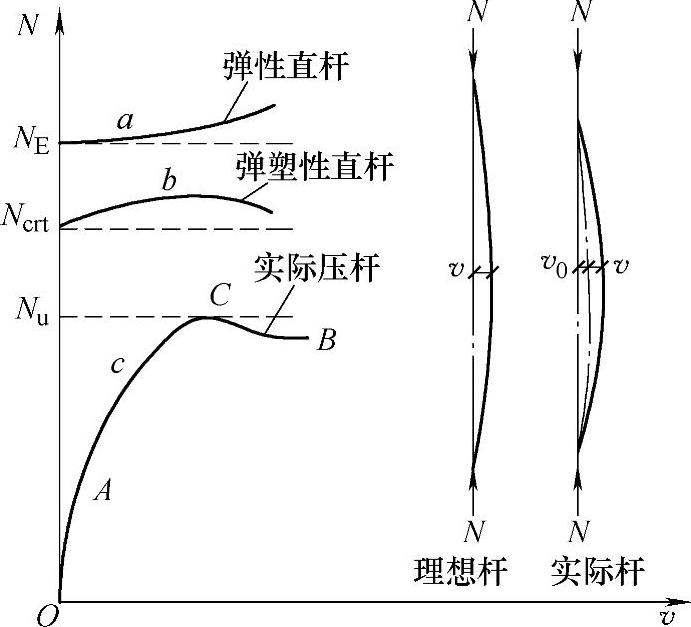
图3-15 压杆的压力挠度曲线

（2）实际轴心受压柱整体稳定计算公式 柱整体不失稳的条件按式（3-9）计算。

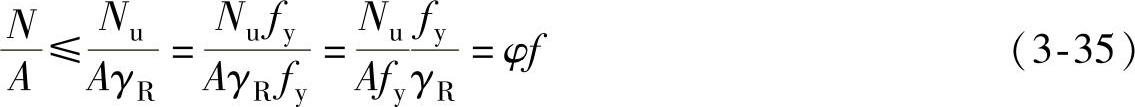
式中 N——轴心受压柱的压力设计值；

A——构件的毛截面面积；

φ——轴心受压构件的稳定系数；

f——钢材的抗压强度设计值；

γ_R——钢材的抗力分项系数。