1.受剪普通螺栓

（1）一个螺栓的设计和承载能力计算

1）抗剪承载力设计值。假设螺栓受剪面上所受的剪应力均匀分布，则单个螺栓的抗剪承载力设计值N^b_v为

式中 n_v——一个螺栓的受剪面数（单剪n_v=1，双剪n_v=2，如图2-21所示）；

d——螺栓杆的直径；

f^b_v——螺栓的抗剪强度设计值，其取值见表2-5。

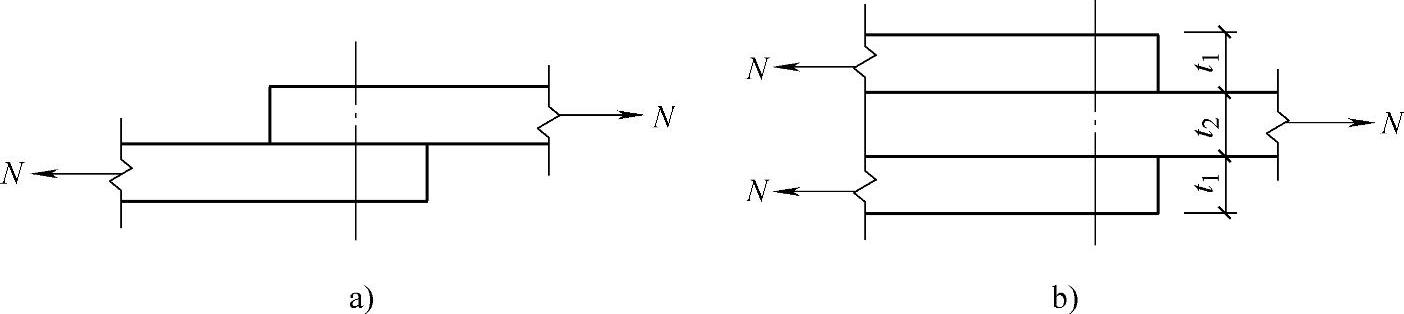
图2-21 受剪螺栓连接的受剪面数

a）单剪 b）双剪

2）承压承载力设计值。假设螺栓孔壁的承压应力沿螺栓直径的投影面均匀分布，则单个螺栓的承压承载力设计值（孔壁不被压坏）N^b_c为

Nb_c=d×∑t×f^b_c （2-11）

式中 ∑t——在同一受力方向承压构件（被连接板件）的较小总厚度（图2-21中取2t₁和t₂中的较小值）；

f^b_c——螺栓的（孔壁）承压强度设计值，取值见表2-5。

可以看出，单个受剪螺栓的承载力设计值应取N^b_v与N^b_c中的较小值N^b_min。

（2）普通螺栓群在轴心力作用下的计算 按照《钢结构设计规范》（GB 50017—2003）规定，每一杆件在节点上和拼接接头的一端，永久螺栓数不宜少于两个，因此螺栓连接中的螺栓一般都是以螺栓群的形式出现。

1）确定螺栓数目。经试验表明，螺栓群的抗剪连接承受轴心力时，螺栓群在长度方向上的各螺栓受力不均匀，如图2-22所示，两端受力大，中间小。连接长度l₁≤15d₀（d₀为螺栓孔直径）时，由于连接工作进入弹塑性阶段后，内力发生重分布，各螺栓受力将逐渐趋于相等，所以可按照平均受力计算。因此，连接一侧螺栓需要的数目为

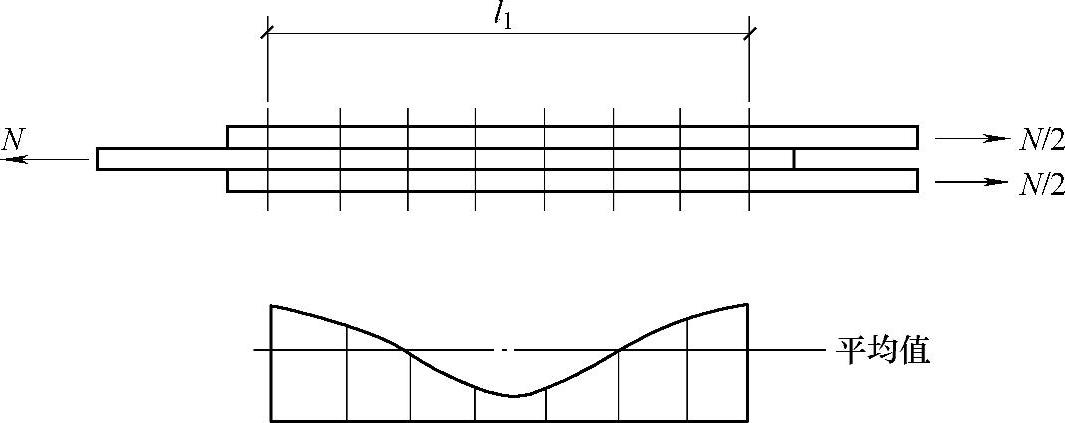
图2-22 长接头螺栓的内力分布

在构件的节点处及拼接接头的一端，当螺栓沿受力方向的连接长度l₁（图2-22）过大时，受力最大的端部螺栓往往先破坏，然后中间螺栓依次向内破坏。所以《钢结构设计规范》（GB 50017—2003）规定，当l₁＞15d₀时，螺栓的承载力设计值N^b_min应乘以折减系数η使其降低，即

当15d₀＜l₁＜60d₀时：

当l₁≥60d₀时：

η=0.7 （2-14）

另外，还需注意，在以下几种情况的连接中，由于连接的工作情况较差，所以我国设计规范规定螺栓或铆钉的数目应较计算增加。

①一个构件借助于填板或其他中间板件与另一构件连接的螺栓（高强度螺栓摩擦型连接除外）或铆钉数目，应较计算增加10%。

图2-23所示为两块厚度不相等钢板的螺栓对接接头，在右端较薄板一侧需设置填板。因为填板一侧的螺栓受力后易弯曲，工作状况比左侧为差，所以右侧螺栓数目应增加10%。

图2-23 用填板的螺栓对接接头

②搭接拼接或用拼接板的单面连接（图2-24），由于接头易发生弯曲，所以螺栓（高强度螺栓摩擦型连接除外）或铆钉数目应相应增加10%。

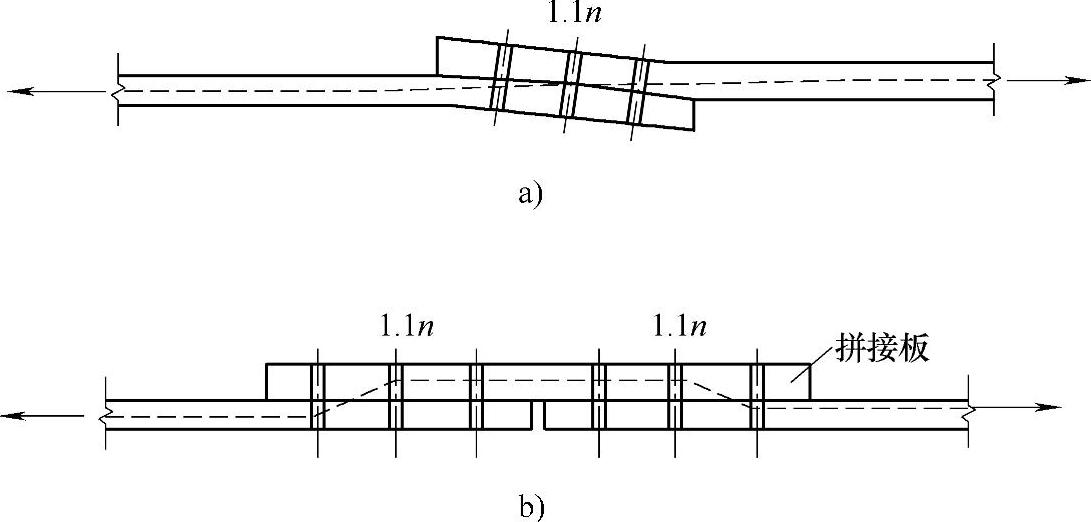
图2-24 搭接接头和单面拼接板连接

a）搭接接头 b）单面拼接板连接

③在构件端部连接中，当通过利用短角钢连接型钢（角钢或槽钢）的外伸肢以缩短连接的长度时（图2-25），在角钢两肢中的一肢上所用的螺栓应比计算数目增加50%。

2）验算净截面强度。为避免构件或连接板由于螺孔削弱而被拉（或压）断，还需要按式（2-15）验算净截面强度：

式中 A_n——构件或连接板的净截面面积；

f——钢材的抗拉（或抗压）强度设计值，按规定的强度设计值选用。

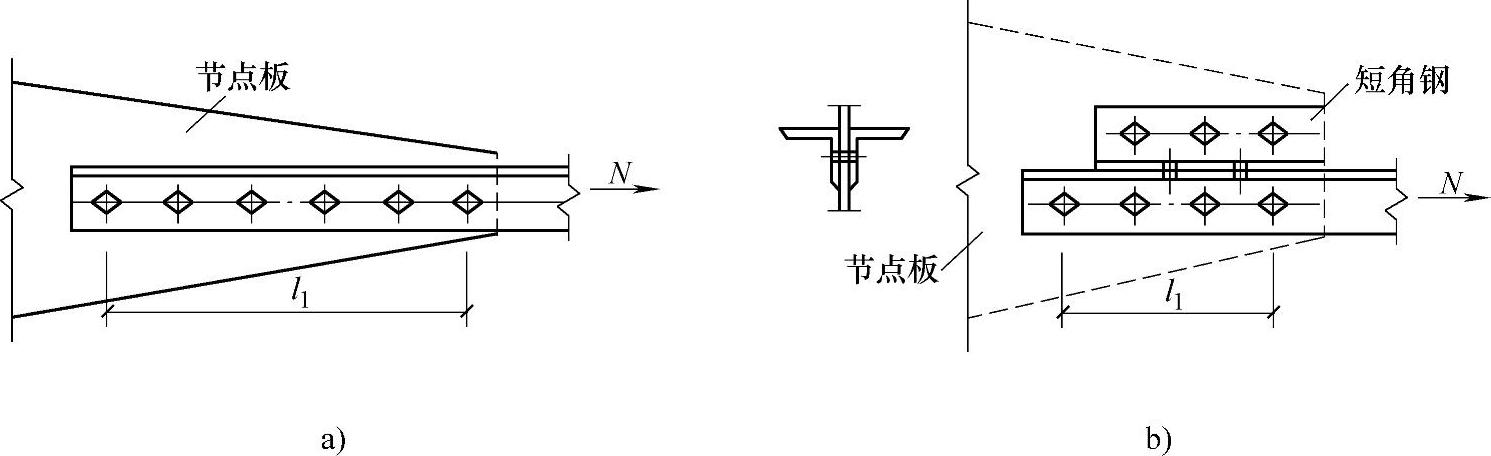
图2-25 角钢构件与节点板的螺栓连接

a）普通构件的端部连接 b）短角钢连接型钢的外伸肢

验算净截面的强度时，应选择构件或连接板的最不利截面，也就是内力最大或螺孔较多的截面。螺栓为并列布置时，如图2-26a所示，构件最不利截面为Ⅰ—Ⅰ截面，其内力最大为N。而截面Ⅱ—Ⅱ和Ⅲ—Ⅲ虽然其板件截面面积相同于Ⅰ—Ⅰ截面，但由于前面螺栓已传递部分力，所以内力分别递减为N-（n₁/n）N和N-[（n₁+n₂）/n]N（n、n₁、n₂分别为连接一侧的螺栓总数和截面Ⅰ—Ⅰ、Ⅱ—Ⅱ上的螺栓数），即都比截面Ⅰ—Ⅰ小。因此，当螺栓孔数未增多时，可以不进行计算。但对连接板（拼接盖板）各截面，由于受力相反，截面Ⅲ—Ⅲ受力最大为N，因此还需按式（2-16）、式（2-17）比较截面Ⅲ—Ⅲ和截面Ⅰ—Ⅰ的净截面面积，以确定最不利截面。

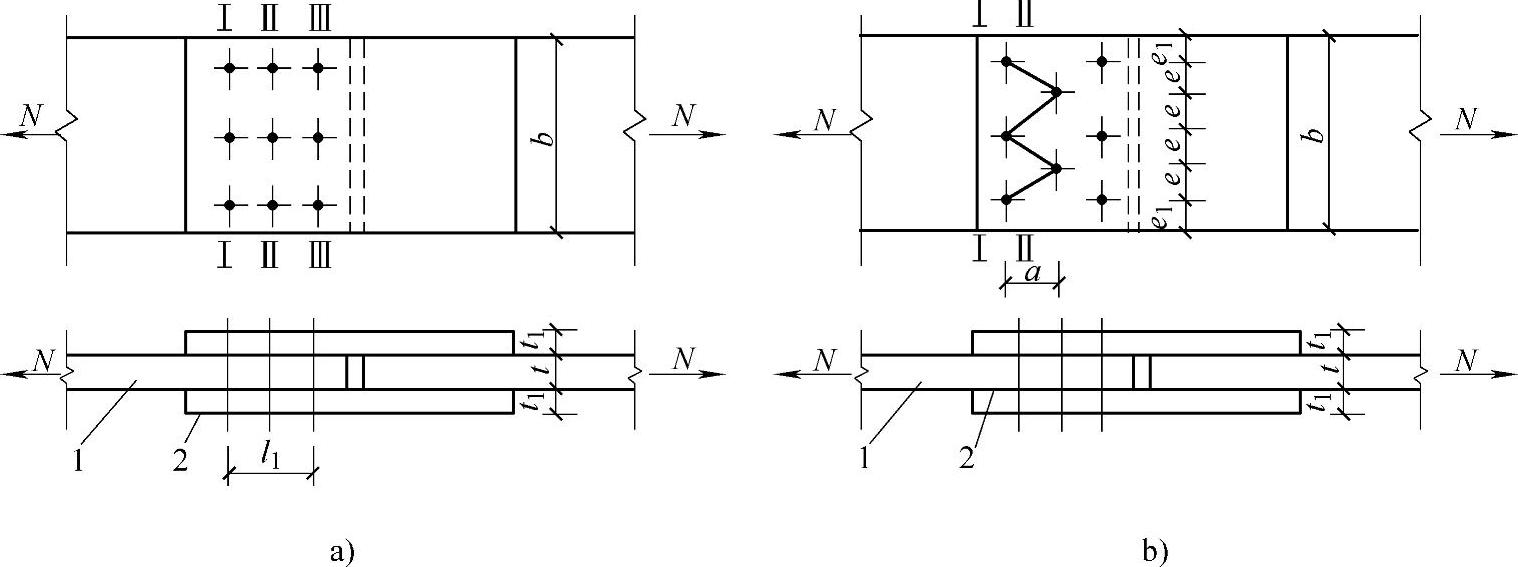
图2-26 螺栓群受轴心力作用

a）螺栓的并列布置 b）螺栓的错列布置

1—板件 2—拼接板

构件截面Ⅰ—Ⅰ：

A_n=（b-n₁d₀）t （2-16）

连接板截面Ⅲ—Ⅲ：

A_n=2（b-n₃d₀）t₁ （2-17）

式中 n₁、n₃——截面Ⅰ—Ⅰ和Ⅲ—Ⅲ上的螺孔数；

t、t₁、b——构件和连接板的厚度及宽度。

当螺栓错列布置时（图2-26b），构件或连接板除可能沿直线截面Ⅰ—Ⅰ破坏外，可能沿折线截面Ⅱ—Ⅱ破坏，由于其长度虽较大，但螺孔较多，因此还需按照式（2-18）计算其净截面面积，以确定最不利截面。

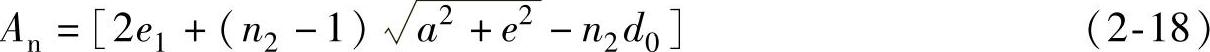
式中 n₂——折线截面Ⅱ—Ⅱ上的螺孔数。

（3）普通螺栓群在扭矩作用下的计算 螺栓群在扭矩作用下，每个螺栓实际受剪计算时假设：被连接构件是绝对刚性的，而螺栓则是弹性的；各螺栓绕螺栓群的形心旋转，其受力大小与到螺栓群形心的距离成正比关系，方向同螺栓到形心的连线垂直，如图2-27所示。

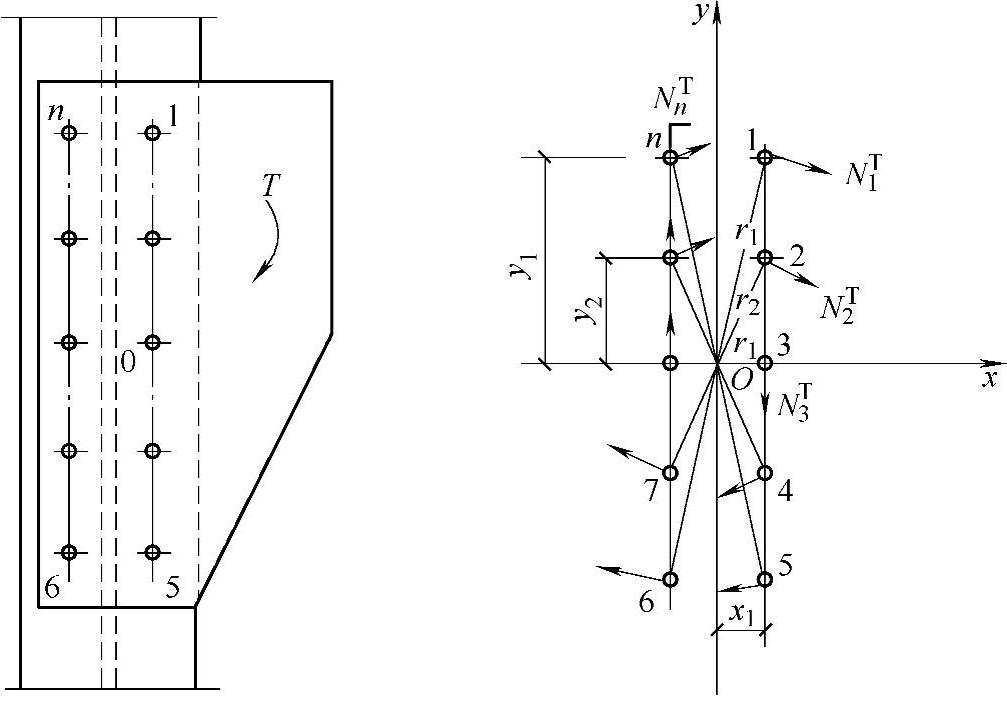
图2-27 扭矩作用下受剪螺栓群的受力情况

设螺栓1、2、…、n到螺栓群形心O点的距离为r₁、r₂、…、r_n，各螺栓承受的力分别为N^T₁、N₂^T、…、N^T_n。由平衡条件得

T=N^T₁r₁+N^T₂r₂+…+N^T_nr_n （2-19）

螺栓受力大小与其距形心的距离成正比，即

将式（2-20）代入式（2-19），得

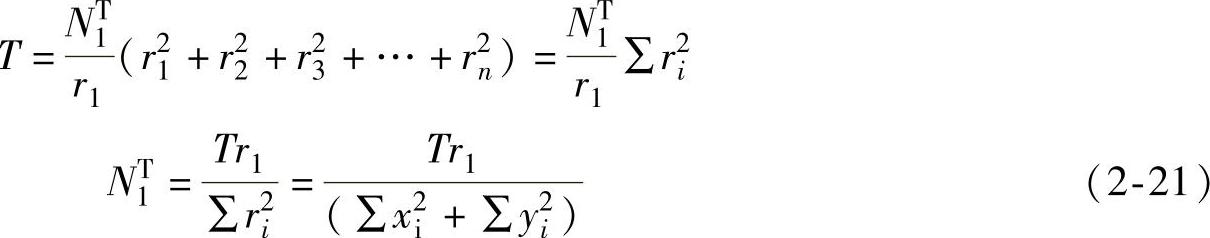
当螺栓群布置在一个狭长带时，若y₁＞3x₁，r₁趋近于y₁，∑x²_i可忽略不计，则式（2-21）可写成

受力最大螺栓所承受的剪力应不大于螺栓的抗剪承载力设计值，即

N^T₁≤N^b_min （2-23）

（4）普通螺栓群在扭矩、剪力和轴心力联合作用下的计算 螺栓群在通过其形心的剪力V与轴向力N作用下（图2-28），每个螺栓受力相同，其值为

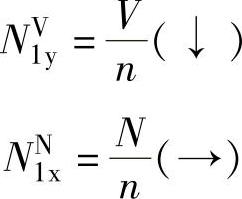
在扭矩T作用下，螺栓1受力最大，将N^T₁分解为水平和竖直方向的分力，即

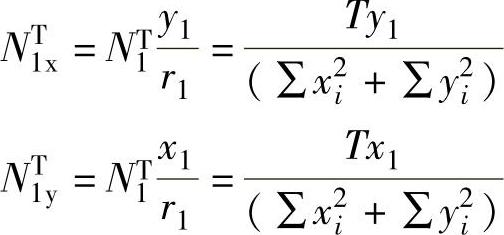
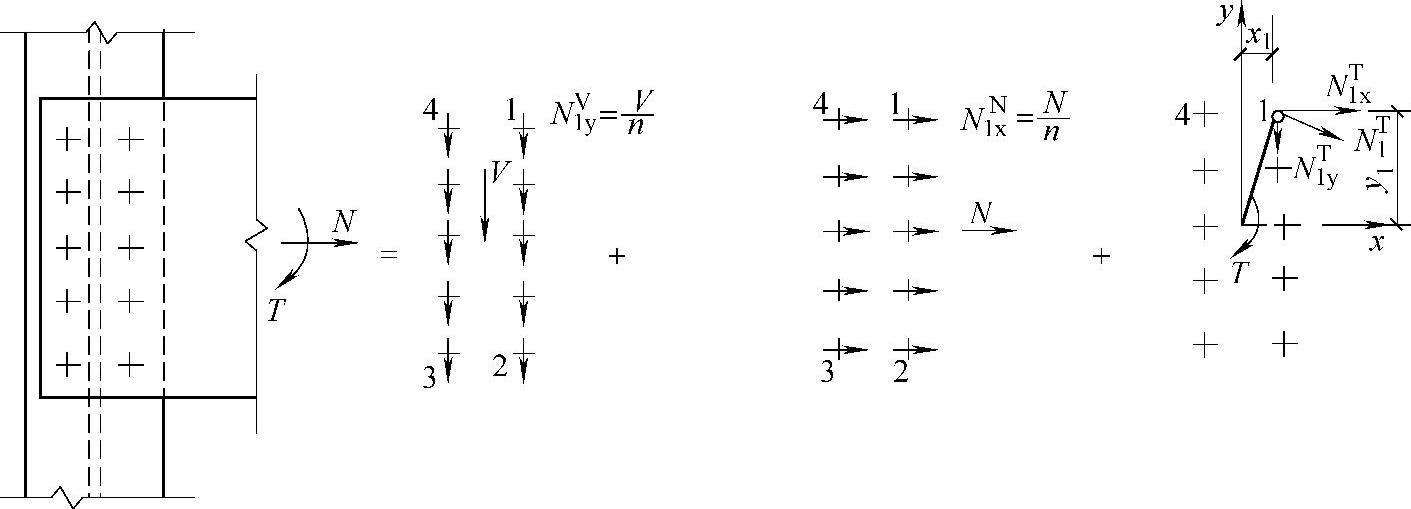
图2-28 扭矩、剪力和轴向力共同作用下受剪螺栓群的受力情况

所以在扭矩、剪力及轴向力共同作用下，螺栓群中受力最大的一个螺栓所承受的合力及强度条件为

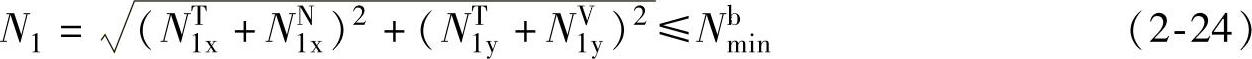
【例2-7】 钢材为Q235的钢板，承受轴心拉力设计值F=560kN，截面为12mm×13mm，采用双盖板和M18、C级普通螺栓连接，螺栓孔径19.5mm。试设计此连接的接头。

【解】 （1）确定连接盖板截面 采用双盖板拼接，盖板截面尺寸选6mm×300mm，与被连接钢板截面面积相等，钢材采用Q235。

（2）确定连接一侧所需螺栓数目及对螺栓合理布置 查表得f^b_v=140N/mm²，f^b_c=350N/mm²。

单个螺栓受剪切承载力设计值为

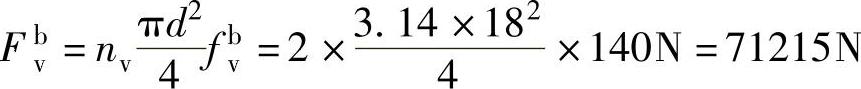
单个螺栓承压力承载力设计值为

Fb_c=d∑tf^b_c=18×12×305N=65880N

F^b_min=Fbc=65880N

则连接一侧所需螺栓数目为

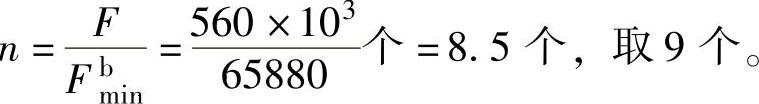
采用如图2-29所示的并列排列，连接盖板尺寸为26×300×490，其布置符合表2-4螺栓的最大、最小容许距离的要求。

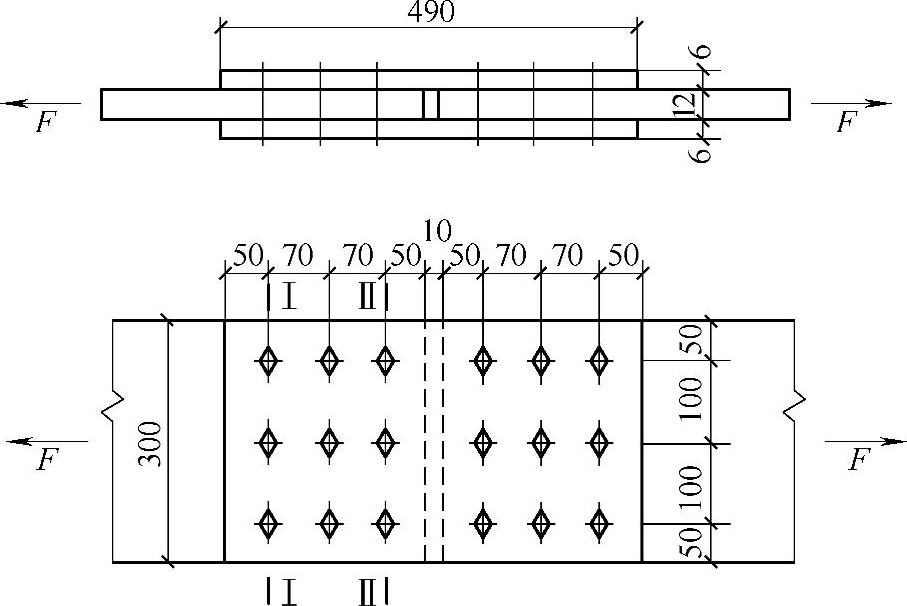
图2-29 螺栓的并列排列（例2-7）(www.daowen.com)

（3）验算连接板件的净截面强度 查表得f=215N/mm²。连接钢板在Ⅰ—Ⅰ截面处受力最大为F，连接盖板则在Ⅱ—Ⅱ截面处受力最大也为F，但因两者材质、截面均相同，故只验算连接钢板。其净截面面积A_n为

A_n=A-n₁d₀t=（300×12-3×19.5×12）mm²=2898mm2

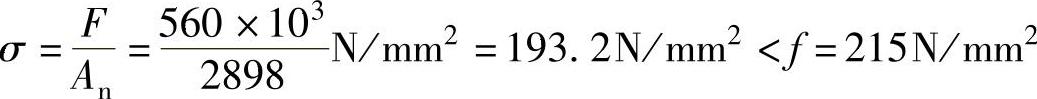
经验算连接钢板净截面强度满足受力要求。

2.受拉普通螺栓

（1）单个普通螺栓的抗拉承载力 抗拉螺栓连接在外力作用下，构件的接触面有脱开趋势，此时螺栓受到沿杆轴方向的拉作用，因此抗拉螺栓连接的破坏形式为栓杆被拉断。

假设拉应力在螺栓螺纹处截面上均匀分布，则单个螺栓的抗拉承载力设计值为

式中 d_e——螺栓的有效直径；

f^b_t——螺栓抗拉强度设计值。

1）螺栓的有效截面面积。如图2-30所示，由于螺纹是斜向的，所以在计算单个螺栓的抗拉承载力时采用的直径，不是净直径d_n，而是有效直径d_e（d_n＜d_e＜d，根据国家标准规定），d_e的取值为

式中 d——外直径；

t——螺距。

2）螺栓垂直连接件的刚度对螺栓抗拉承载力的影响。螺栓受拉时，一般不可能使拉力正好作用于螺栓轴线上，而是通过与螺杆垂直的板件使之传递。图2-31所示为T形连接，如果连接件的刚度较小，受力后与螺栓垂直的连接件会发生变形，从而会产生杠杆作用，使螺栓有被撬开的趋势，螺杆中的拉力增加并且产生弯曲现象。考虑杠杆作用时，螺杆的轴心力为

N_t=N+Q （2-27）

式中 Q——由于杠杆作用对螺栓产生的撬力。

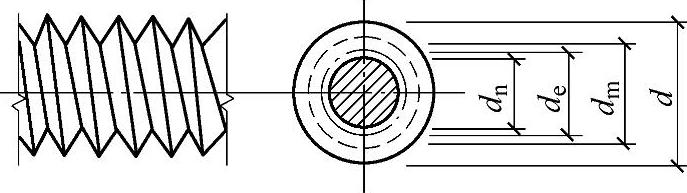
图2-30 螺栓螺纹处的直径

图2-31 受拉螺栓的撬力

撬力的大小与连接件的刚度有关，连接件的刚度越小，其撬力越大；同时撬力也与螺栓直径和螺栓所在位置等相关。由于确定撬力比较复杂，我国现行钢结构设计相关规范为了简化，规定普通螺栓抗拉强度设计值f^b_t取为螺栓钢材抗拉强度设计值f的0.8倍（即f_t=0.8f），以考虑撬力的影响。此外，在构造上也可采取相应的措施以加强连接件的刚度，比如设置加劲肋（图2-32），这可以减小或者消除撬力的影响。

（2）普通螺栓群轴心受拉 如图2-33所示，螺栓群在通过利用其形心的轴心力作用时，一般假定每个螺栓平均受力，则连接所需螺栓数为

式中 N^b_t——个螺栓的抗拉承载力设计值。

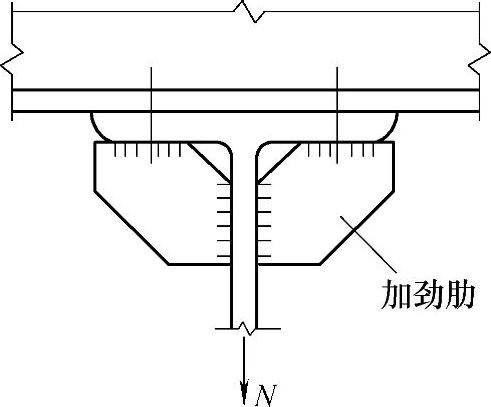
图2-32 设置加劲肋的T形螺栓群连接

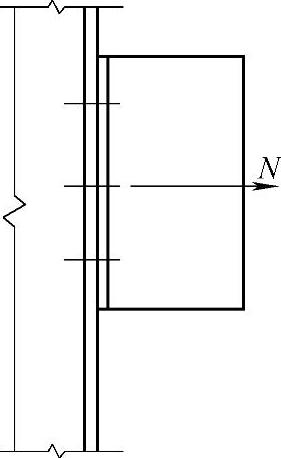
图2-33 螺栓群承受轴心拉力

（3）普通螺栓群弯矩受拉 螺栓群受弯矩M的作用，如图2-34所示。由于普通螺栓在旋拧时的预拉力较小，弯矩的作用下，有使被连接板件上部与之分离的趋势，它的旋转中心将由螺栓群的形心逐渐下移，旋转中心上部螺栓受拉。假设旋转中心在顺弯矩方向最外排螺栓的形心轴处，各排螺栓所受拉力的大小与其到旋转中心（图中为最下排螺栓）的距离成正比，因而最上排螺栓所受拉力最大。其值可以根据以下平衡条件求得，即

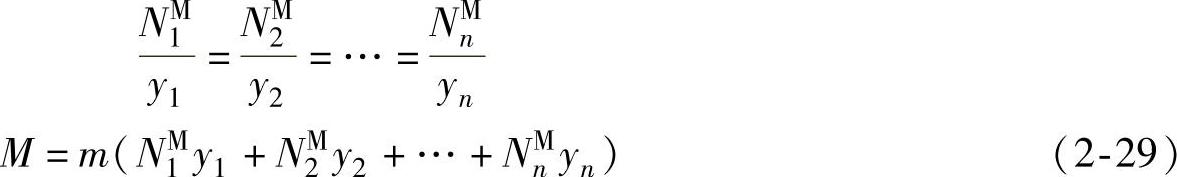
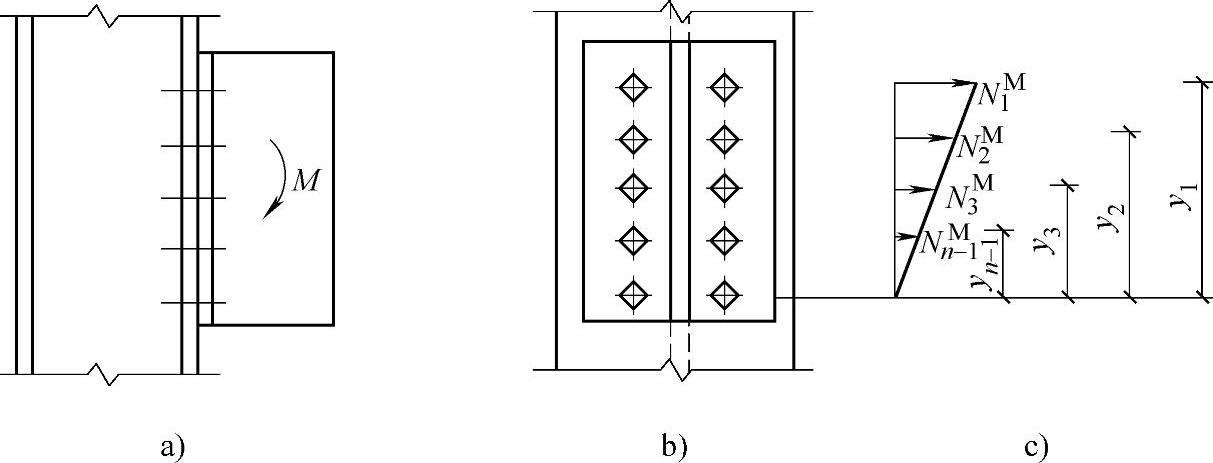
图2-34 螺栓群受弯矩作用

a）螺栓群受弯矩M的作用 b）连接件受力趋势 c）旋转中心上部螺栓受拉

最上排一个螺栓所受的拉力为

式中 y₁——最外排螺栓到旋转中心的距离；

y_i——每排螺栓到旋转的距离；

m——螺栓的列数。

要使连接不发生破坏，需要符合的条件为

（4）普通螺栓群偏心受拉 图2-35所示为钢结构中较为常见的一种螺栓连接形式（如屋架下弦端部与柱的连接）。螺栓群受偏心拉力F与剪力V作用。若剪力由焊接在柱子上的支托承受，则螺栓群只承受偏心拉力F的作用。在螺栓群承受偏心力作用的计算时，需要区分两种情况。

1）小偏心受拉情况。对于小偏心受拉情况（图2-35a），所有的螺栓都承受拉力作用，端板与柱翼缘有分离趋势。因此在计算时，轴心拉力N由各螺栓均匀承受；而弯矩M则引起以螺栓群形心O处水平轴为中和轴的三角形应力分布，使上部螺栓受拉，下部螺栓受压；叠加之后全部螺栓都为受拉。最大和最小受力螺栓的拉力计算公式以及须满足的设计要求为（y都由O点算起）

N_max=N/n+Ney₁/∑y²_i≤N^b_t （2-32）

N_min=N/n-Ney₁/∑y²_i≤0 （2-33）

式（2-32）表示的是最大受力螺栓的拉力不超过一个螺栓的承载力设计值；式（2-33）则表示全部螺栓均受拉，不存在受压区。根据式（2-33）可得N_min≥0时的偏心距e≤∑y²_i/（ny_i）。令ρ=∑y²_i/（ny₁）为螺栓有效截面组成的核心距，即e≤p时为小偏心受拉。

2）大偏心受拉情况。偏心距e较大，弯矩M也较大时，端板底部将会出现受压区（图2-35b），中和轴位置将下移。为简化计算，可近似的将中和轴假定在（弯矩指向一侧）最外一排螺栓轴线O′处。所以，按照同小偏心情况相似的方法，写出对O′处水平轴的弯矩平衡方程（e′和y自O′点算起，最上排螺栓“1”的拉力最大），即

N₁/y′₁=N₂/y′₂=…=N_i/y′_i=…N_n/y′_n

Ne′=N₁y′₁+N₂y′₂+…+N_iy′_i+…+N_ny′_n

=（N₁/y′₁）y′21+…+（N_n/y′_n）y′_n2

=（N_i/y′_i）∑y′_i2

则N₁=Ne′y′₁/∑y′_i2≤N^b_t（N_i=Ne′y′_i/∑y′_i2） （2-34）

【例2-8】 设有一梁一柱，柱上设有承托板，假设承托承受全部剪力，钢材均为Q235，承受的竖向剪力V=380kN，弯矩M=60kN·m（均为设计值）。试设计梁端部和柱翼缘的C级螺栓连接。

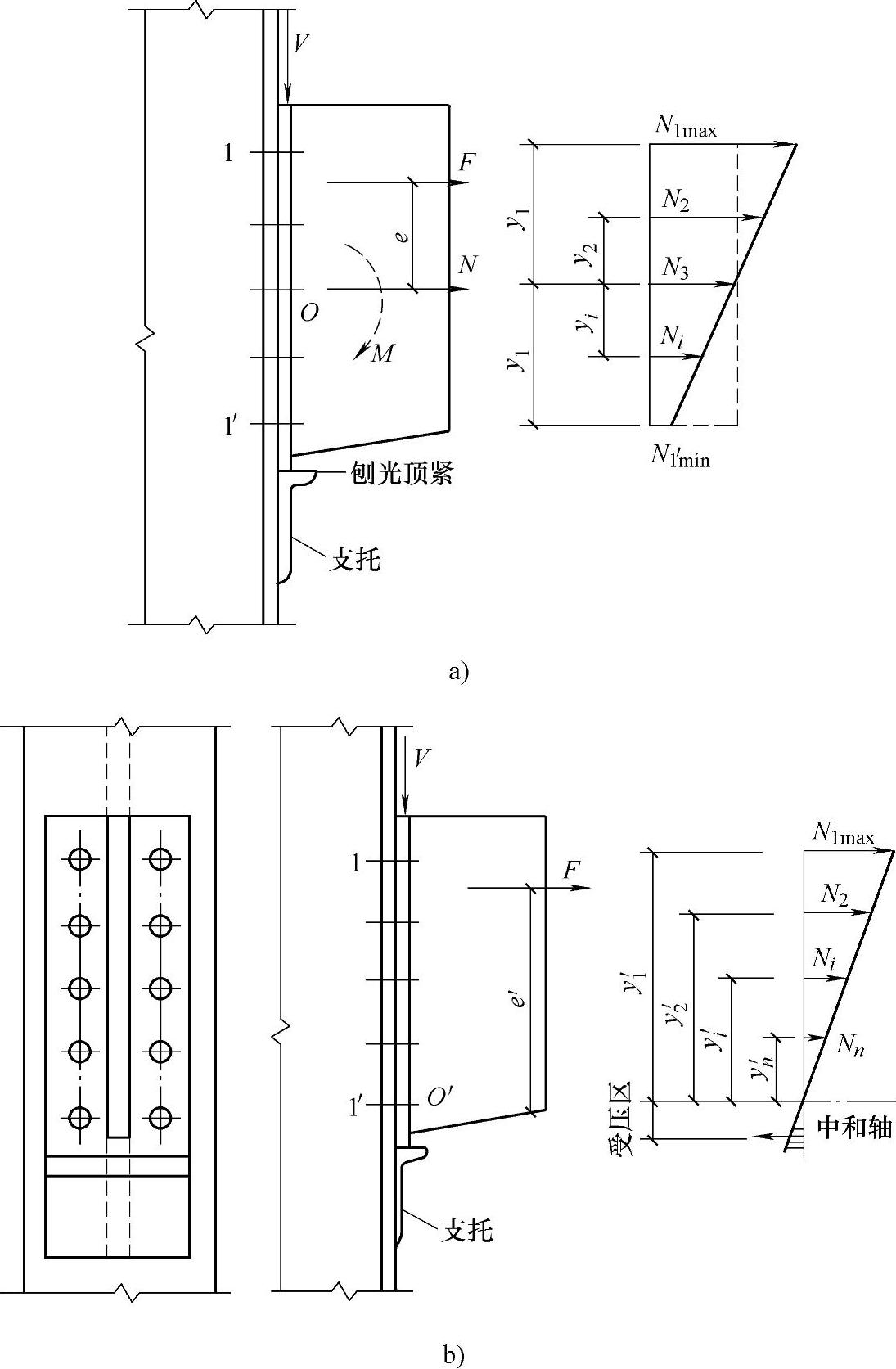
图2-35 螺栓群受偏心力作用时的受拉螺栓

a）小偏心受拉情况 b）大偏心受拉情况

【解】 初选10个M20螺栓，d₀=22mm，并按图2-36所示的尺寸排列。中距布置较大，以增加抵抗弯矩的能力。

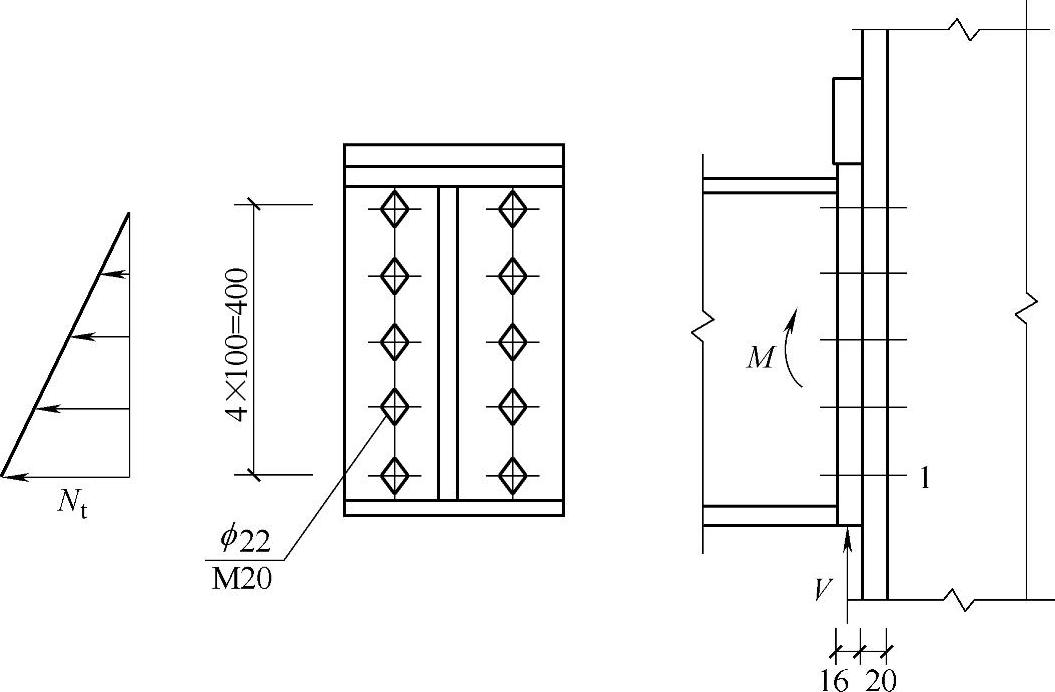
图2-36 梁端部和柱翼缘的螺栓连接（例2-8）

单个螺栓的抗拉承载力设计值为

N_t^b=A_ef^b_t=244.8×170N=41616N=41.6kN

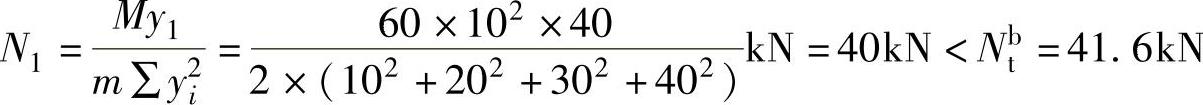
3.同时受拉剪螺栓连接

（1）同时承受剪力和拉力的普通螺栓连接计算 图2-37所示的连接，把作用力V移到螺栓群的形心时，螺栓群同时受剪力V与弯矩M=Ve的作用。

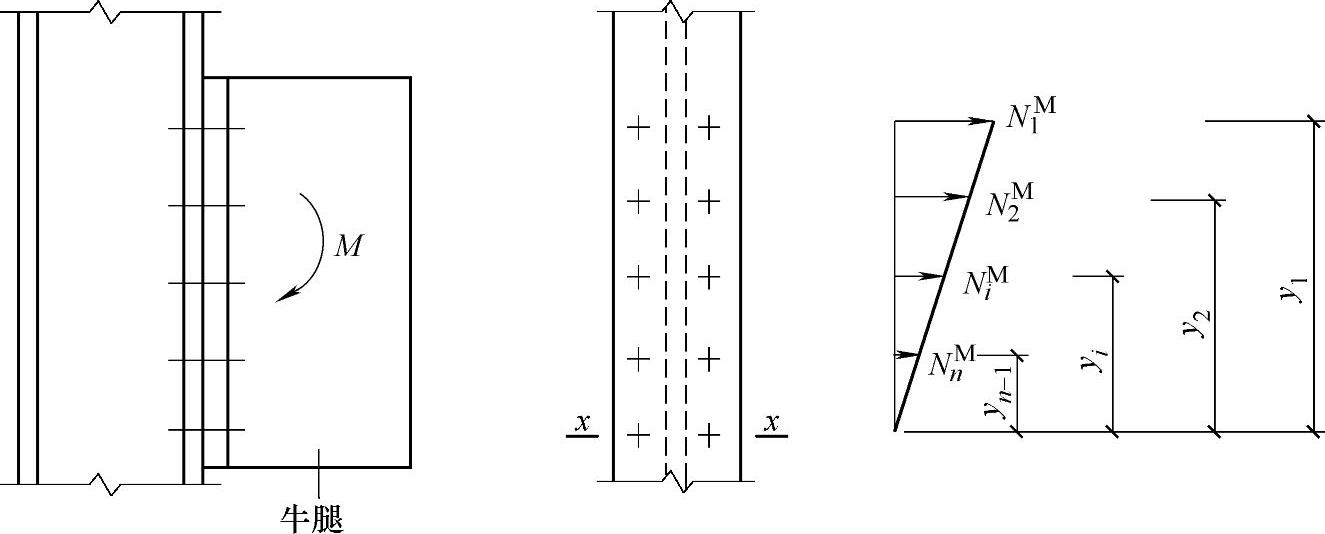
图2-37 剪力和拉力共同作用下螺栓群的受力情况

1）支托只作为安装时所用的临时支撑，不传递剪力。在剪力V的作用下，各个螺栓均匀受力，每个螺栓受力为

在弯矩M的作用下，螺栓群中受力最大的螺栓应按式（2-29）计算其所受的拉力，即。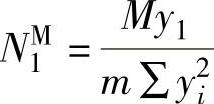

螺栓在拉力与剪力共同作用下安全工作的条件应符合式（2-36）和式（2-37）。

式中 N^b_v、N^b_c、N^b_t——单个螺栓的抗剪、承压和抗拉承载力设计值。

2）支托是永久性的，此时剪力则由支托承受，弯矩由螺栓承受。支托与柱翼缘采用角焊缝连接，按照式（2-38）计算。

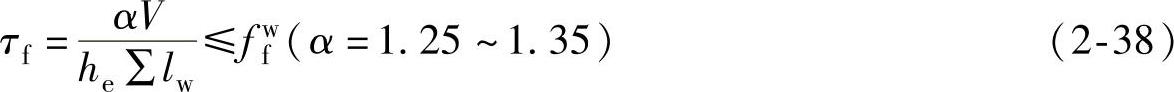
【例2-9】 图2-38所示为柱翼缘与短横梁的连接，Q235B钢材，电弧焊，焊条E43型，剪力V=260kN，e=120mm，螺栓为C级，梁端竖板下有支托。根据承托承受全部剪力V与不承受V两种情况设计此连接。

【解】 （1）承托承受全部剪力 V=260kN，螺栓群只承受由偏心力引起的弯矩，M=Ve=260×0.12kN·m=31.2kN·m。根据弹性设计法，可假设螺栓群旋转中心在弯矩指向的最下排螺栓的轴线上。设螺栓为M20（A_e=244.8mm²），则受拉螺栓数n_f=8，连接中为双列螺栓，用m表示，一个螺栓的抗拉承载力设计值为

N_t^b=A_ef^b_t=244.8×170×10^-3kN=41.62kN

螺栓的最大拉力为

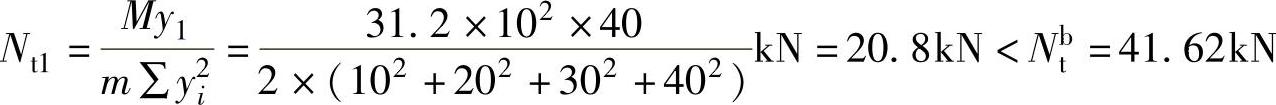
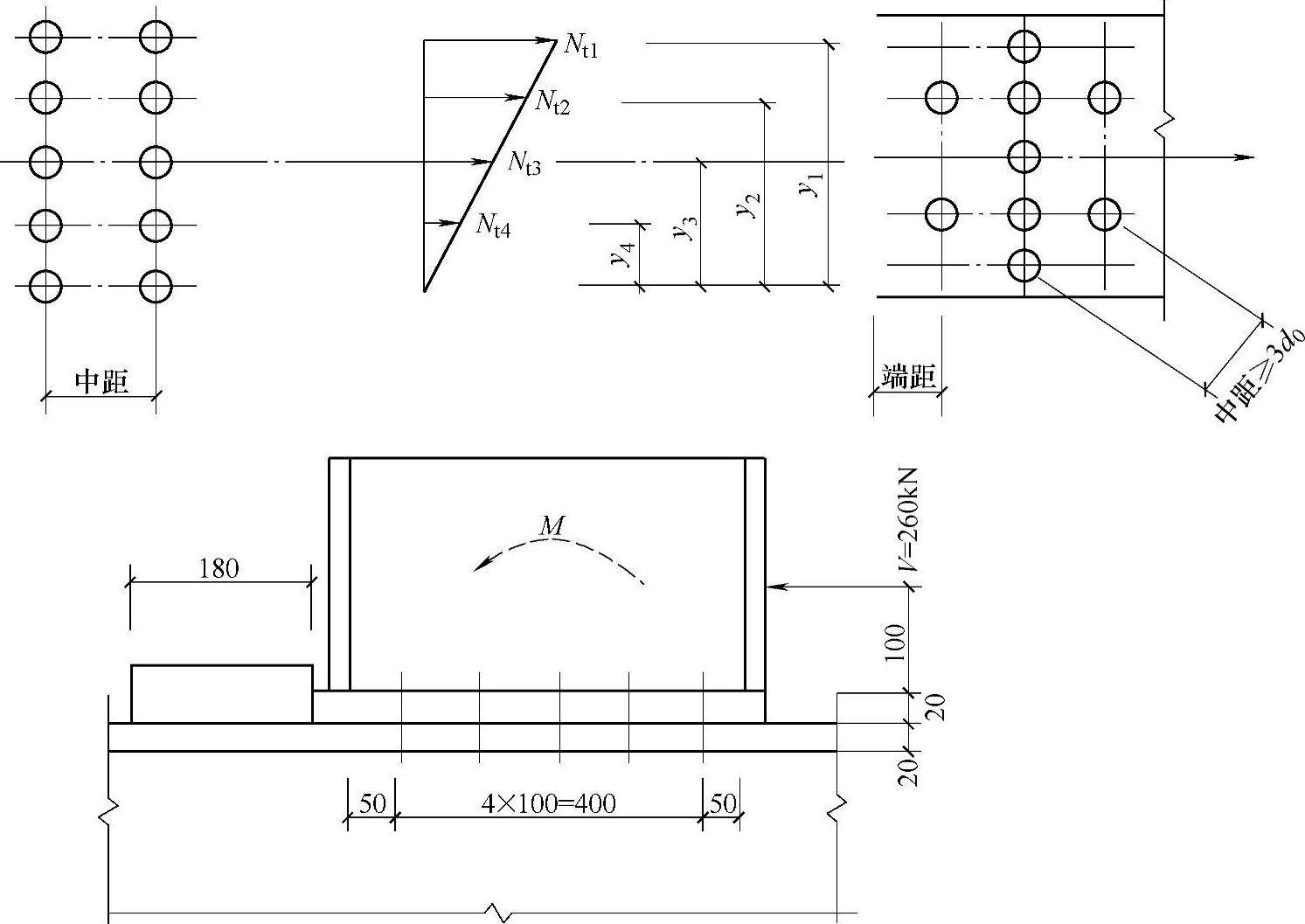
图2-38 短横梁与柱翼缘的连接（例2-9）

设支托与柱翼缘连接角焊缝为两面侧焊，并且取焊脚尺寸h_f=10mm，焊缝应力为

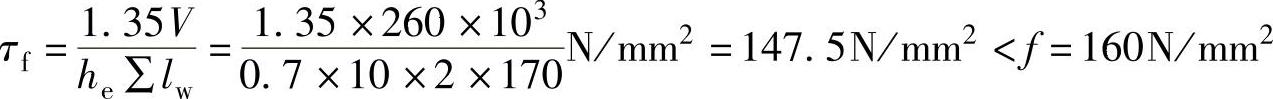
常数1.35是考虑剪V对支托与柱翼缘连接角焊缝的偏心影响。

（2）不考虑支托承受剪力V 螺栓群同时承受剪力V=260kN和弯矩M=31.2kN·m作用，则一个螺栓承载力设计值为

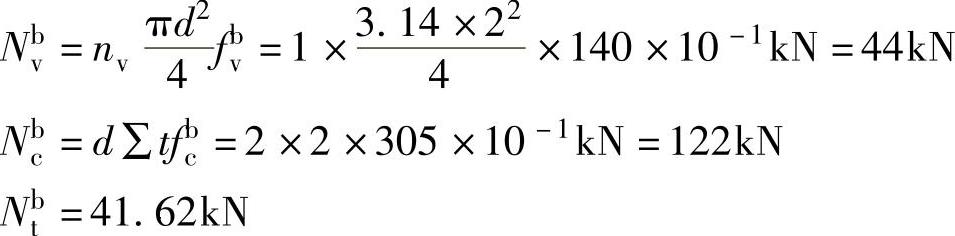
一个螺栓的最大拉力N_t=20.8kN

一个螺栓的剪力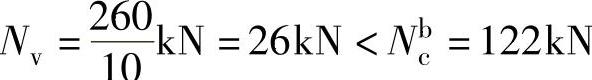

剪力和拉力联合作用下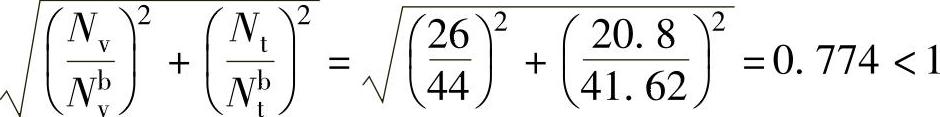，满足要求。