拐角装药，是指装药在传爆路径上存在夹角的装药。

5.1.2.1 拐角效应

当爆轰波从小尺寸装药向大尺寸装药传播时，由于离散而使爆轰波在部分区域内产生偏离正常爆轰的状态，在拐角处发生绕射，产生一个不稳定的爆轰区，这一区域内有不爆区和弱爆区，称拐角效应。其临界特性表现为一定装药尺寸下的拐角角度和一定角度下的装药尺寸。

图5.6中，r*称为拐角半径，d*为拐角距离。当装药尺寸d＜dc+d *时，爆轰波不能拐过拐角传播；当d＞dc+d *时，爆轰波可以传播，但需经过r*长度后才能达到正常爆轰，这种现象称为拐角效应，拐角效应存在延迟爆轰现象。令dcc=dc+d*为临界尺寸，则d＞dcc 是拐角传播的装药条件。拐角装药爆轰波传播临界特性研究包括两个内容：一个是研究在一定拐角角度下，爆轰波沿拐角传播的最小尺寸；另一个是研究在一定装药尺寸条件下，爆轰波能拐过的最大角度。在爆炸网络技术研究中，一般采用等沟槽尺寸设计爆炸逻辑网络，且沟槽的最大拐角一般也不会超过90°，因此在拐角装药爆轰波传播临界尺寸研究中，主要研究爆轰波拐过直角时的最小装药尺寸。

图5.6　拐角效应示意图

5.1.2.2 拐角装药临界尺寸研究

分别设计加工了沟槽尺寸为0.7 mm × 0.7 mm、0.6 mm × 0.6 mm、0.5 mm × 0.5 mm、0.4 mm × 0.4 mm的试验基板，在设计装药密度为1.77 g/cm3的条件下研究其拐角装药爆轰波传播的临界尺寸，典型测定装置如图5.7所示。其中，每一块基板中含有18个拐角，沟槽间距最小为5 mm，最大为15 mm，最短直线沟槽长度为15 mm。

图5.7　小尺寸装药爆轰波拐角传播临界尺寸测定装置

（a）测定装置示意图；（b）沟槽尺寸为0.6 mm × 0.6 mm测定装置实物

按所设计的约束条件及试验环境温度，分别用LD-14B雷管从输入端起爆测定装置，观察爆轰波在沟槽中的传播情况，试验装置爆炸效果图如图5.8、图5.9所示，试验结果见表5.1。

图5.8　全约束条件下试验基板爆炸效果图

（a）沟槽宽和深0.5 mm；（b）沟槽宽和深0.4 mm

图5.9　无盖板约束试验基板爆炸效果图

表5.1　爆炸逻辑网络沟槽拐直角装药临界尺寸爆轰试验结果

由表5.1可知，在装药密度为1.77 g/cm3时，所研究炸药在小尺寸沟槽装药条件下拐直角传播的临界尺寸约为0.5 mm × 0.5 mm。对于超细化HMX，装药密度对小尺寸装药爆轰波拐角传播的临界尺寸影响较大，提高装药密度，爆轰波传播的临界尺寸明显减小。此外，环境温度对临界尺寸基本没有影响，沟槽装药在常温及低温下均能可靠传爆。理论上，约束条件对拐角装药爆轰波传播的临界尺寸会有影响，无盖板约束条件下的临界尺寸应大于全约束条件下的临界尺寸，但试验结果表明盖板约束条件对临界尺寸无明显影响。因此，综合分析表5.1中的试验数据可知，在全约束条件下该沟槽装药拐直角传播的临界尺寸不会大于0.5 mm × 0.5 mm，以此沟槽尺寸为依据，采取裕度设计的方法设计爆炸逻辑网络。

5.1.2.3 小尺寸拐角装药爆轰延迟现象物理模型与数学方程

由于拐角效应，小尺寸非直线装药爆轰波在通过拐角时，存在一段非稳态爆轰区或引爆点偏离拐角点的延迟引爆现象，由此造成爆轰波延迟传播现象[5～7]。

王树山通过高速摄影实验[8]，对某挠性炸药的小尺寸拐角装药爆轰波传播特性进行了研究，证实了爆轰波通过小尺寸装药拐角时存在一段非稳态爆轰区，其长度与装药尺寸和拐角角度有关。他还通过对不同拐角角度、不同装药尺寸下爆轰波传播时间的测量，发现装药尺寸越小，拐角角度越大，爆轰延迟时间越长，当拐角大于某一角度时，甚至可能造成熄爆，据此给出所研究炸药的爆轰延迟时间与拐角角度的经验关系式。

小尺寸拐角装药爆轰延迟时间现象的理论基础就是小尺寸装药的拐角效应现象，爆轰波在通过拐角时，存在一段非稳态爆轰区或引爆点偏离拐角点的延迟引爆现象，由此造成爆轰波延迟传播。非稳态爆轰区越长，爆轰延迟时间越长。因此，小尺寸拐角装药爆轰延迟现象的物理模型与拐角效应现象的物理模型相同，如图5.6所示，其中不爆区与弱爆区的长度就是延迟引爆距离。

爆轰波从直线向拐角传播方向的示意图如图5.10所示。

图5.10　小尺寸装药爆轰波拐角传播示意图

（a）垂直三通；（b）α 拐角

图5.10中，在OC = OB情况下，爆轰波沿拐角传播的时间tOB大于沿直线传播的时间tOC，即tAB＞tAC ，δt=tAB-t AC 称为延迟时间，δt是表达延迟现象的特征量，称为拐角装药爆轰延迟时间，单位为ns。通常情况下，α在0～π之间变化，α=π/2则更常见。

影响小尺寸爆轰传递的主要参数：

爆炸网络基板的几何及性能参数：沟槽尺寸（等宽深）d、基板密度ρs、声速as、拐角角度α。

沟槽装药的性能参数：装药密度ρ、反应区特征厚度Δ、爆速D、爆轰产物膨胀系数β。

介质的初始状态：如压强P0，由于空气冲击波压强比0P大得多，故可忽略0P的影响。再者，在爆轰试验的瞬间，由于基板与盖板用螺钉紧固，对沟槽装药形成强约束，外界环境对爆轰波的传播几乎无影响。

此外，结合拐角效应的物理模型（图5.4）分析可知，含拐角装药的沟槽尺寸d越小，爆轰波通过拐角绕射并趋于稳定所经历的弱爆区会越长，拐角爆轰延迟时间越长。当d小于临界尺寸dcc时，拐角爆轰延迟时间将趋于无穷大，出现熄爆；当d大于极限尺寸dL时，几乎不产生爆轰延迟现象。因此，d的取值范围为dcc≤d≤dL 。

当爆轰波经拐角发生绕射时，其爆轰延迟时间tδ可表述为

在基板材料和装药品种以及装药工艺一定的情况下，以上分析的各物理量中，除爆速D以外都是独立自变量。爆速D在一定范围内随着装药尺寸的变化而变化，但考虑到它与极限爆速DJ之间存在的关系，即D是DJ与d的函数，在已经列出物理量d的情况下，可以考虑用DJ替代D进行分析。因此式（5-24）可写为

取Δ、ρ、DJ为基本参量，对式（5-25）进行无量纲化可得

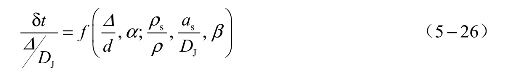
在给定装药条件下，上式右端后三个无量纲量可以视为常数，隐含在函数f1(α)和参数m中，则表达式可进一步简化为

即

随着拐角角度α的不断增大，最终会出现熄爆现象，取αc表示出现爆轰波熄爆的最小拐角角度，称为临界拐角角度，则当α≥αc 时出现熄爆，即f1(α)→∞。因此拐角角度α的取值范围为0＜α＜αc 。分析α对δt的影响，还应有f1(0)=0，当α不断向0°趋近时需满足收敛。

结合上述边界条件和收敛性要求，假设函数，则式（5-28）可写为

(www.daowen.com)

显然，。临界拐角角度随装药尺寸的增大而增大，其极限值为π，方便起见，本研究取αc=π进行讨论，即f1(π)→∞。则上式可写为

如果给定α，那么，的比例系数为。若，则的比例系数为。这样，决定关系的经验参数有三个：k0、m、n。

式（5-30）就是拐角延迟时间的理论表达式，设计不同装药尺寸不同拐角角度的网络基板进行试验，通过对数据的拟合可得待定参数k0、m及n，并最终获得δt～d～α三者之间的普适关系式。

5.1.2.4 小尺寸拐角装药爆轰延迟时间的试验研究

1. 小尺寸拐角装药爆轰延迟时间测试方法

采用薄膜探针法测量拐角装药爆轰延迟时间[9]，探针安装原理如图5.11所示。试验中采用5个探针，探针1作为触发探针，安装在沟槽装药分岔点之前，探针2～5作为测试探针，安装在以沟槽装药拐角中心为圆心的两段等距圆弧上，两段圆弧的半径分别为15 mm、30 mm。试验基板起爆后，第一个探针接通，触发测试仪计时，当爆轰波传播到第2、3、4、5探针时，各传感器分别记录下爆轰波到达的时间，即t2、t3、t4、t5。分别对所记录的时间按Δt24=t4-t 2，Δt35=t5-t 3进行处理，就可以得到爆轰波通过拐角时的延迟时间。

图5.11　拐角装药爆轰延迟测试原理

2. 试验结果与分析

确定式（5-25）中的每一个参数，获得普适的半经验关系式需要大量的实验数据支持。根据直线装药爆速测试结果及小尺寸装药临界尺寸试验研究结果，采用细颗粒JO-9C传爆药，在平均装药密度为ρ=1.77g/cm3时，沟槽装药极限尺寸dL=1.2mm ，拐直角传播临界尺寸dcc=0.50mm ，根据上述推导过程可知该表达式的适用范围应为0.50mm≤d ≤1.2mm 。设计爆炸逻辑网络装药沟槽尺寸为0.8mm×0.8mm ，由于爆炸逻辑网络设计中拐角角度一般不超过120°，加工拐角角度分别为30°、45°、60°、90°、120°的拐角试验基板进行测试。基板装药效果图如图5.12所示。

图5.12　基板沟槽装药效果图

（a）90°；（b）30°；（c）45°；（d）60°；（e）120°

按图5.11所示的原理安装薄膜电极传感器，进行拐角装药爆轰延迟时间测试，安装薄膜电极传感器后的基板如图5.13所示。基板沟槽尺寸为0.8 mm × 0.8 mm时，拐角装药爆轰延迟时间测试结果见表5.2。其中，采取了从示波器直接读取直线和拐角间爆轰波传播时间差的方法确定拐角装药爆轰延迟时间Δt24、Δt35。

图5.13　拐直角沟槽装药薄膜电极传感器装配图

表5.2　沟槽尺寸为0.8 mm × 0.8 mm时拐角装药爆轰延迟时间测定结果

由表5.2可知，随着拐角角度增大，爆轰波拐角延迟时间增大，通过数据处理，依据最小二乘法原理，按式（5-30）进行拟合，得到k0、m和n分别为：k0=62，m=0.6，n=0.5。即得到沟槽尺寸为0.8 mm × 0.8 mm时拐角装药爆轰延迟时间与拐角角度关系的半经验关系式：

利用半经验关系式（5-31）计算所得延迟时间和对应角度的延迟时间测试值如表5.3所示，拟合曲线如图5.14所示。

表5.3　装药尺寸为0.8 mm × 0.8 mm时拐角装药爆轰延迟测试与计算对比

图5.14　沟槽尺寸为0.8 mm × 0.8 mm时拐角延迟时间与拐角角度的关系

从图5.14中不难看出，测试结果与利用式（5-31）计算所得结果变化趋势基本吻合，说明利用此半经验关系式计算出的拐角延迟时间与试验结果基本一致。为了验证此研究方法及拟合过程所得参数的合理性，本研究还设计了装药尺寸为d=0.6mm ，拐角角度分别为45°、60°、90°、120°的拐角网络基板。同样采用细颗粒JO-9C传爆药，在平均装药密度为ρ=1.77g/cm3时，沟槽装药极限尺寸dL=1.2mm ，拐直角传播临界尺寸dcc=0.50mm ，装药尺寸d=0.6mm 符合使用要求，测试结果如表5.4所示。

表5.4　沟槽尺寸为0.6 mm × 0.6 mm时拐角装药爆轰延迟时间测定结果

续表

从表5.4中的数据可以看出，随着拐角角度的增大，爆轰波拐角延迟时间增大，且在α=2π/3时爆轰波未能拐过拐角，出现熄爆现象。

将d=0.6mm ，k0=62，m=0.6，n=0.5代入式（5-30），可得拐角装药爆轰延迟时间与拐角角度的关系式：

由表5.4试验测试结果及由式（5-32）计算得出的拐角装药爆轰延迟时间与拐角角度关系的对比见表5.5，建立的拐角装药爆轰延迟时间与拐角角度的关系如图5.15所示。

表5.5　装药尺寸为0.6 mm × 0.6 mm时拐角装药爆轰延迟测试与计算对比

从图5.15可以看出，在沟槽尺寸为0.6 mm × 0.6 mm时，拐角装药存在明显的爆轰延迟现象，且随拐角角度增加，爆轰延迟时间增大。理论值与实验值相近，拐角延迟时间随拐角角度的变化趋势相符，说明式（5-30）的理论推导具有合理性。

图5.15　沟槽尺寸为0.6 mm × 0.6 mm时拐角延迟时间与拐角角度的关系

对比表5.2和表5.4的测试结果可知，与d=0.8mm 的网络基板相比，在相同拐角角度下，d=0.6mm 时的拐角爆轰延迟时间普遍较大，甚至在α=2π/3时还不能传爆，说明装药尺寸的减小导致了拐角熄爆现象的临界角度提前出现，此结果符合物理模型。

分别将k0=62，m=0.6，n=0.5代入式（5-30），可计算出不同装药尺寸下的拐角延迟时间，计算结果如表5.6所示，曲线如图5.16所示。

表5.6　不同装药尺寸下的拐角装药爆轰延迟

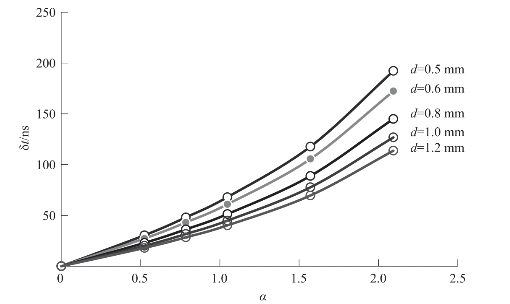
图5.16　不同装药尺寸下拐角延迟时间与拐角角度的关系

图5.16预报了临界尺度dcr=0.5mm 、极限尺度dL = 1.2 mm等的延迟时间δt随α 变化的曲线。由式（5-32）的推导过程可知，该公式的适用范围为dcc＜d＜dL ，即在dcc邻域δt发生强间断，当d→0.5 mm时δt→max ，在d＜0.5 mm时δt→∞。从图中可以看出，多种不同装药尺寸下拐角延迟时间均随拐角角度的增大而增大，在相同的拐角角度下拐角延迟时间随装药尺寸的增大而减小，符合一般的物理规律，说明本研究的分析过程及所得半经验公式是合理的。由此所得的半经验关系式在爆炸逻辑网络及其他导爆、传爆装置的设计过程中有一定的工程实用意义。