3.3.2.1 计算模型

图3.20　电流流经SCB的过程

电流流经SCB的过程如图3.20所示，当脉冲电流经过两端的引线流入SCB时，SCB将电能转换为引发含能材料作用的其他能量，其中SCB的电阻起了主要作用，由于铝电极与掺杂硅之间采用大面积接触，降低了接触电阻。所以换能元电阻的核心由桥区部分决定，为了计算SCB的静态电阻，还需要作如下假设：

（1） 垂直于电流方向的任一截面的电流密度均匀。

（2） 忽略电极与焊点之间的接触电阻，以及两端引线的电阻。

3.3.2.2 数学表达

导体的电阻值取决于导体的材料性质和几何尺寸，对于截面积恒定的导体，其电阻与长度l成正比，与截面积s成反比，可表示为[15]

式中，l为导体的长度（cm）；s为导体的截面积（cm2）；ρ为与材料特性有关的常数，称为电阻率（Ω·cm），是电导率σ的倒数。

对于SCB而言，一定温度下，掺杂浓度ND又决定了SCB的电阻率ρ，即R = R（l，w，δ，θ，ρ）。

以SCB桥区的长度方向为x轴，宽度方向为y轴，左边界中点为坐标原点建立直角坐标系，如图3.21所示，分别对Ⅰ、Ⅱ两部分积分求电阻。沿x轴SCB桥区的横截面积可表示为

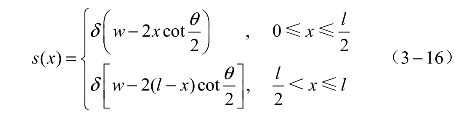
图3.21　SCB阻值计算坐标图

根据电阻计算式（3-1），可得

当时，将式（3-16）代入式（3-17）得Ⅰ部分电阻随长度的变化率为

当时，将式（3-13）代入式（3-14）得Ⅱ部分电阻随长度的变化率为

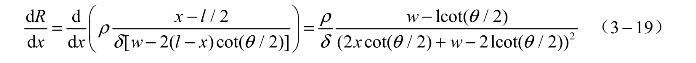(www.daowen.com)

分别对式（3-15）、式（3-16）积分并求和得电阻表达式：

式中，，为薄膜的膜电阻或方阻。令，称为长宽比，则式（3-20）可简化为

式（3-21）即双V形SCB电阻的理论计算式。通过上式可知，当方阻确定时，SCB的电阻只与长宽比ω和V形角θ 有关，ω越大，电阻R越大，V形角θ 的设计需满足一定范围，即2arctanω＜θ≤π。当θ=π时，为方形桥，R为最小值，R=Rsω ；当θ=2arctanω 时，R的阻值为无穷大。

3.3.2.3 电阻率ρ 随温度的变化

对于半导体材料，导带中的电子和价带中的空穴两种载流子均参与导电，对于N型半导体，电子浓度远远大于空穴浓度，空穴对电流的贡献可以忽略[16]。所以N型硅电阻率的理论计算公式可表示为[17]

式中，q=1.6×10-19，为载流子（电子）电量；n为载流子（电子）浓度；μn为载流子（电子）迁移率。载流子浓度和迁移率均与硅中杂质浓度和温度有关，即SCB电阻率随杂质浓度和温度而异。

在不同温度区域，固态SCB载流子浓度的表达式为

式中，Tb为饱和电离区温度上限。

液态硅的电阻率比固态硅电阻率低1个数量级，可达到10-4 Ω·cm的数量级，这样的导电水平类似于一些金属，如水银。这是因为液态硅的4个价电子都能参与导电，从而液态硅的电子密度为

式中，NSi=5×1022cm-3为硅原子密度。文献［18］把液态半导体电阻率当作金属处理：

式中，σ(Tmelt )=12300（Ω·cm）-1；Tmelt为SCB的熔点（1 684 K[19]）。

综上所述，电阻率可以表示如下：

式中，Tg = 2 880 K为SCB的汽化点。