为了验证上述换能模型，本章针对金属桥带电火工品经常使用的能量加载方式，对不同的金属桥带换能元分别进行5 min恒流激励实验和50 ms恒流激励实验。

3.2.2.1 5 min恒流激励实验

1. 实验样品

为了研究金属桥带形状、散热面积对恒流激励下熔断电流的影响，本章选择两种不同尺寸的金属桥带换能元进行实验，具体形状如图3.12所示，尺寸如表3.7所示。

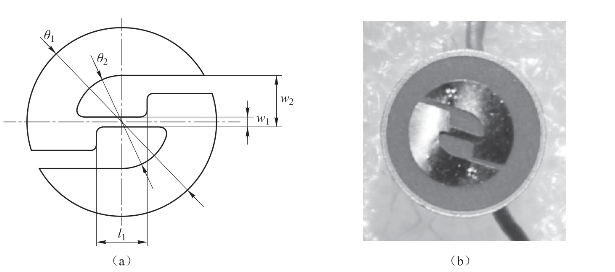
图3.12　实验用金属桥带

（a）S形桥带结构示意图；（b）S形桥带样品

表3.7　S形桥带尺寸

2. 实验方法和结果

实验方法采用的是D-最优化法，实验所用的仪器设备和实验电路图同3.1.2.2节。本实验取电流变为“0”，电压不再发生变化看作恒流激励情况下桥带熔断的判据，如图3.13所示。

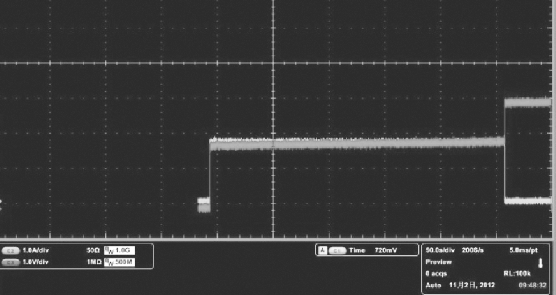
图3.13　恒流激励下桥带熔断时示波器上的信号

按照D-最优化法和上述判据测试出桥带换能元的临界熔断电流ˆ0μ和标准误差ˆ0σ，然后按照正态分布模型计算出99.9%熔断电流和0.1%熔断电流，如表3.8所示。本章定义99.9%熔断的电流为全熔断电流，0.1%熔断的电流为全不熔断电流。

表3.8　5 min恒流激励时金属桥带的临界熔断电流实验结果

3. 实验与理论对比(www.daowen.com)

按照式（3-9）及式（3-10）的差分表达式，利用MATLAB软件计算桥带的临界熔断电流值，并将其与实验结果进行对比，如表3.10所示。计算所用的桥带的参数如表3.7所示，玻璃塞子的参数如表3.9所示，桥带的熔化温度取其熔点。

表3.9　玻璃材料的物化参数

表3.10　5 min恒流激励时桥带临界熔断电流的理论计算值与实验值对比

由表3.10可知，临界熔断电流的理论计算值与实验值的误差在6%以内，两者非常吻合，所以用上述方法来计算金属桥带的临界熔断电流值是比较合理的，这为金属桥带换能元的设计提供了一定的理论指导。

3.2.2.2 50 ms恒流激励实验

实验样品和方法同3.2.2.1节，实验所用设备如图3.14所示。

图3.14　阵列式火工品测试系统点火控制台与光靶

D-最优化法测试金属桥带在50 ms恒流激励情况下的临界爆发电流和标准差，按照3.2.2.1节中的方法计算全不爆发电流和全爆发电流，结果如表3.11所示。

表3.11　50 ms恒流激励下金属桥带的临界爆发电流实验结果

按照式（3-9）及式（3-10）的差分表达式，利用MATLAB软件计算50 ms恒流激励时金属桥带的临界爆发电流值，并将其与实验结果进行对比，如表3.12所示。计算中用到的桥带爆发点取桥带的汽化温度。

表3.12　50 ms恒流激励时桥带的临界爆发电流的理论计算值与实验值对比

由表3.12可知，50 ms临界爆发电流的理论计算值与实验值的误差在5%以内，两者非常吻合，所以可以用上述方法计算金属桥带的50 ms临界爆发电流。