3.1.2.1 临界熔断电流实验

1. 实验样品

为了验证方程（3-3），本书对桥丝（Ni80/Cr20）直径为9 μm、12 μm、16 μm、20 μm和25 μm，基体材料为塑料和玻璃，基体直径分别为4.7 mm和4.4 mm的两种桥丝换能元进行实验，样品具体形状和尺寸如图3.5和表3.1所示。

图3.5　桥丝换能元件结构

（a）双电极塑料基体桥丝换能元外形；（b）双电极塑料基体桥丝换能元俯视图；（c）单电极玻璃基体桥丝换能元外形；（d）单电极玻璃基体桥丝换能元俯视图

表3.1　桥丝换能元参数

续表

2. 实验方法

主要的感度实验方法有升降法、兰利法、步进法和OSTR 法等。升降法是火工品和火炸药界应用最广的感度实验方法。这种方法操作简单，但是GJB 337—1987指出使用升降法时要首先确定样本量、初始刺激量和步长，而初始刺激量和步长的选择依赖于对期望值和标准差的某种先验知识；兰利法的实验程序规定了一种按当前的响应与否的实验条件，分析从实验开始至当前所获得的数据，确定下一个刺激量的规则，它虽然克服了升降法的上述缺点，但没有成熟的计算标准误差的方法；步进法一般需要用8个以上的刺激量做实验，且每个刺激量下实验样本量至少25发才能得到比较好的参数估计值，这样需要的样本量就太大了。

1989年Neyer根据D-最优化设计理论，提出了Neyer D-最优化感度实验方法，把实验安排、数据处理、似然函数方程以及下一个刺激量的选择统一考虑，使得在每个刺激量上获得的数据含有最大的信息，减少了实验次数。该方法根据实验目的和数据分析来选择实验点，不仅使得在每个实验点上获得的数据含有最大的信息量从而减少实验次数，而且使数据的统计分析具有一些较好的性质。该方法从测试样品的数据中获取最充分的统计信息，并能利用前面全部的测试结果来计算下一个刺激水平，但它需要利用计算机进行详细的计算以得出刺激水平。为了用最少的样本量得到最好的期望估计和标准差估计，本书选择D-最优化法进行实验。

实验测试设备如图3.6所示，包括Agilent E3634A恒流稳压源、TEK TDS7104示波器、TCPA300放大器、TCP312电流探头、1 Ω标准电阻等。测试装置如图3.7所示。实验时首先将单刀双掷开关1扳到a侧，将标准电阻R接入电路形成闭合回路，调整恒流源的输出电流，调到合适的值之后，按下“output off”按钮，然后再将开关1扳到b侧，将换能元件2接入电路，按下恒流源上的“output on”按钮，形成闭合回路，为换能元件通电5 min，同时示波器5通过电压探头4和电流探头3记录换能元两端的电压和电路中的电流。5 min后判断换能元件是否熔断，然后根据D-最优化法程序给出的下一发刺激量，再次接通标准电阻回路，重新调整恒流源的输出电流并换样品，依此类推，直至实验结束。

图3.6　 实验测试设备

（a）恒流稳压源；（b）信号采集设备

图3.7　桥丝换能元临界熔断电流测试实验电路

1—单刀双掷开关；2—换能元件；3—电流探头；4—电压探头；5—示波器；R—1 Ω标准电阻

3. 实验结果

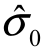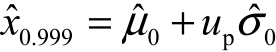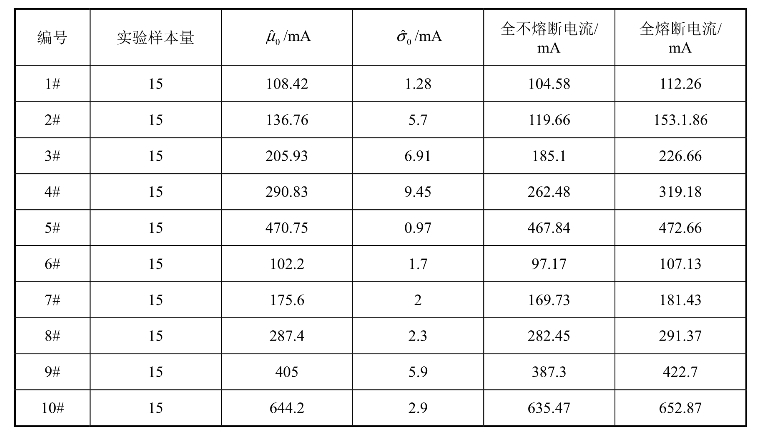
本实验将电流变为“0”视为熔断，按照D-最优化法程序可得出不同桥丝换能元的50%熔断电流和标准差，然后经过计算得出99.9%熔断电流和0.1%熔断电流，如表3.2所示。就换能元实验而言，在均值附近，样品临界刺激水平常被认为服从正态分布。所以计算99.9%熔断电流的公式为：；计算0.1%熔断电流的公式为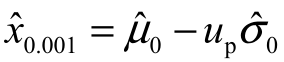：。其中，u0.999=3.09。此外，本书中定义99.9%熔断的电流为全熔断电流，0.1%熔断的电流为全不熔断电流。

表3.2　桥丝换能元临界熔断电流实验结果

4. 实验与理论计算对比

按照式（3-3）计算实验所用的Ni80/Cr20桥丝换能元件的临界熔断电流，并将理论计算值与实验所得值进行对比（计算中所用到的参数见表3.3），结果如表3.4所示。(www.daowen.com)

表3.3　Ni80/Cr20材料参数

从表3.4可以看出，桥丝换能元临界熔断电流的理论计算值与实验值的误差都在15%以内，所以由式（3-4）来计算桥丝换能元的临界熔断电流是可行的；同一种桥丝直径下，玻璃基体桥丝换能元的临界熔断电流比塑料基体的大，这是由于玻璃的导热性比塑料好。

表3.4　桥丝换能元临界熔断电流实验与理论计算对比

3.1.2.2 临界爆发电压实验

针对桥丝换能元在电容放电加载下的临界爆发电压实验，同样选择了10种不同的样品分别进行实验，实验样品的具体参数如表3.1所示。

1. 实验方法

实验采用D-最优化法，所用仪器主要包括ALG-CM储能放电起爆仪（图3.8）、信号采集设备［TEK TDS7104示波器、TCPA300放大器、TCP312电流探头、电压探头，见图3.6（b）］、47 μF钽电容等，测试装置如图3.9所示。实验时首先将换能元件2接入电路，然后闭合开关a，接通充电回路，对钽电容1进行充电。当充到所需要的电压值时断开开关a，闭合开关b，接通放电电路，对桥丝换能元2进行放电，同时示波器5记录电路中的电流和桥丝换能元2两端的电压。根据示波器上记录的电压、电流信号以及换能元有无火花判断桥丝换能元是否爆发。当电流信号变为“0”，电压信号不再变化，同时桥丝换能元上观察到火花时，即认为桥丝爆发了，否则没有爆发。然后断开开关b，换另一发样品，依此类推，直至完成D-最优化法的实验量。

图3.8　储能放电起爆仪

图3.9　换能元件临界爆发电压测试实验电路

1—47 μF钽电容；2—换能元件；3—电流探头；4—电压探头；5—示波器

2. 实验结果

本实验将电流变为“0”，电压不再发生变化看作桥丝在电容放电加载下的爆发判据，如图3.10所示。

图3.10　电容放电加载情况下桥丝爆发时示波器上的信号

按照D-最优化法测试出10种桥丝换能元的临界爆发电压和标准误差，然后按照正态分布模型计算出99.9%爆发电压和0.1%爆发电压，如表3.5所示。本章定义99.9%爆发的电压为全爆发电压，0.1%爆发的电压为全不爆发电压。

表3.5　桥丝换能元临界爆发电压实验结果

3. 实验与理论计算对比

按照式（3-9）计算桥丝换能元件的临界爆发电压，并将理论值与实验值对比，结果如表3.6所示，计算所用到的参数见表3.3。

表3.6　桥丝换能元临界爆发电压实验与理论计算值对比

从表3.6可以看出，样品爆发电压的理论计算值与实验值的误差都在15%以内，所以由式（3-9）来设计满足某一爆发电压的桥丝换能元的尺寸是可行的；同一直径下，塑料基体桥丝换能元的临界爆发电压比玻璃的高，这是因为同一直径下，塑料基体换能元的桥丝较长，电阻较大，所以所需的电压较高。