钢管穿过磁化线圈时会发生如下两种电磁感应现象：

1）当钢管在横向漏磁检测磁化器内运动时，钢管切割磁力线而在其内部形成感生涡流。

2）钢管磁介质在管头进入磁化线圈和管尾离开磁化线圈时，由于磁化线圈的磁通总量发生急剧变化，线圈中会产生感生电流。

1.钢管内产生的感生涡流

钢管横向缺陷漏磁检测方法采用穿过式线圈产生轴向磁化场，并在磁化线圈内布置检测传感器。当钢管沿着轴向移动时，处于磁化线圈内的钢管段被磁化至近饱和状态，如存在缺陷将在钢管表面产生泄漏磁场，然后被磁敏感元件拾取并依次转换为模拟信号和数字信号，最终由计算机信号处理系统实施报警和分类。

如图5-1所示，以钢管轴线为中心建立圆柱坐标系。沿着钢管运动方向，以磁化线圈为中心将钢管划分为进入区和离开区，在磁化线圈中施加如图所示的磁化电流，磁力线分布特征为：在进入区磁力线从空气中进入钢管，并在磁化线圈中部汇聚，然后在离开区折射入空气中。

如图5-1所示，将磁感应强度矢量B（r，z）分解为轴向分量B_z（r，z）和径向分量B_r（r，z），即

B（r，z）=B_z（r，z）+B_r（r，z） （5-1）

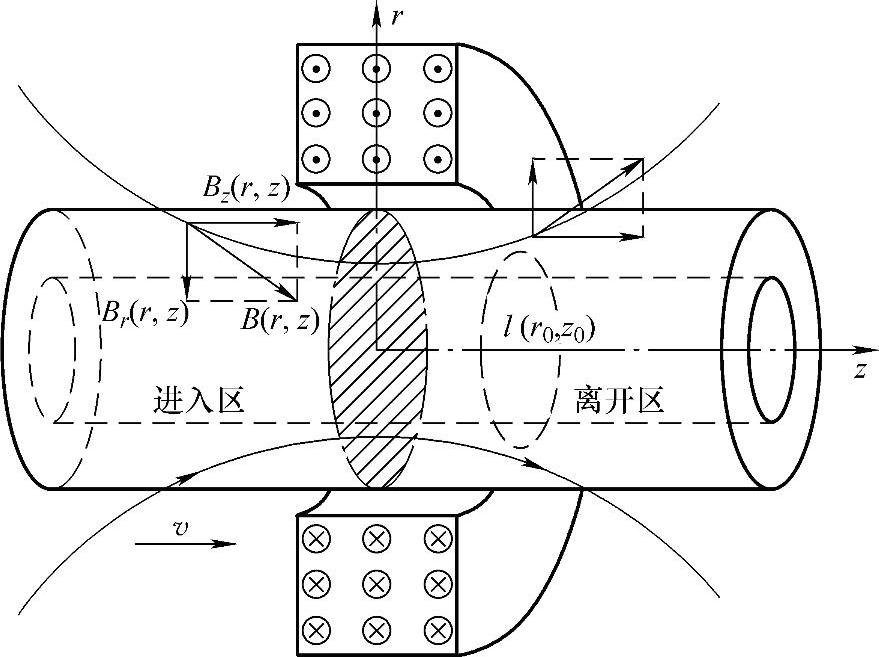
图5-1 钢管漏磁检测系统磁化场分布

从图5-1中可以看出，轴向分量B_z（r，z）在进入区和离开区方向一致，沿着钢管前进方向，其强度在进入区逐渐增大，并在磁化线圈中部达到极大值，之后在离开区逐渐减小。径向分量B_r（r，z）在进入区方向指向钢管内部，并在磁化线圈中部发生转变，在离开区方向指向钢管外部。

为了研究与钢管同轴圆环l（r₀，z₀）的涡流分布，设圆环半径为r₀，轴向位置为z₀。根据楞次定律，当圆环移动时，轴向分量B_z（r，z）的强度变化导致圆环磁通量也发生改变，从而在圆环中产生感生电动势。因磁化场为轴对称，建立圆环感应电动势ε（r₀，z₀）方程为

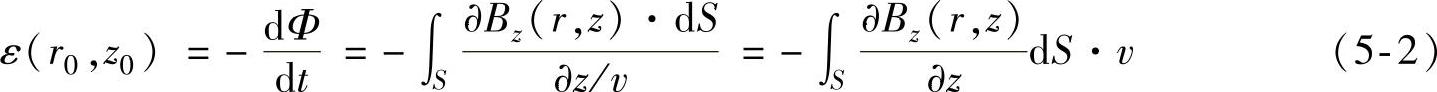
式中，Φ为圆环通过磁通量；S为圆环面积；v为钢管运行速度。

由式（5-2）可知，感应电动势ε（r₀，z₀）与钢管运动速度v成正比。设圆环l（r₀，z₀）的线电导率为γ，进一步得到钢管圆环上感生涡流J（r，z）方程为

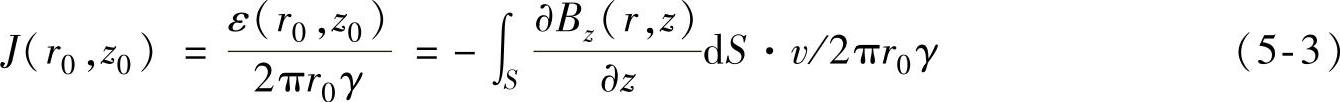
根据式（5-3），沿钢管前进方向，在进入区，轴向分量强度逐渐增强，感生涡流方向与原磁化电流方向相反；在磁化线圈中间位置，由于轴向分量变化率为零，故此部位无感生涡流产生；在离开区，轴向分量强度由中间最大值逐渐减小，于是形成与原磁化电流方向相同的感生涡流，最终钢管中感生涡流分布如图5-2a所示。如果改变磁化电流方向，根据式（5-3），同样可得出钢管内感生涡流分布，如图5-2b所示。

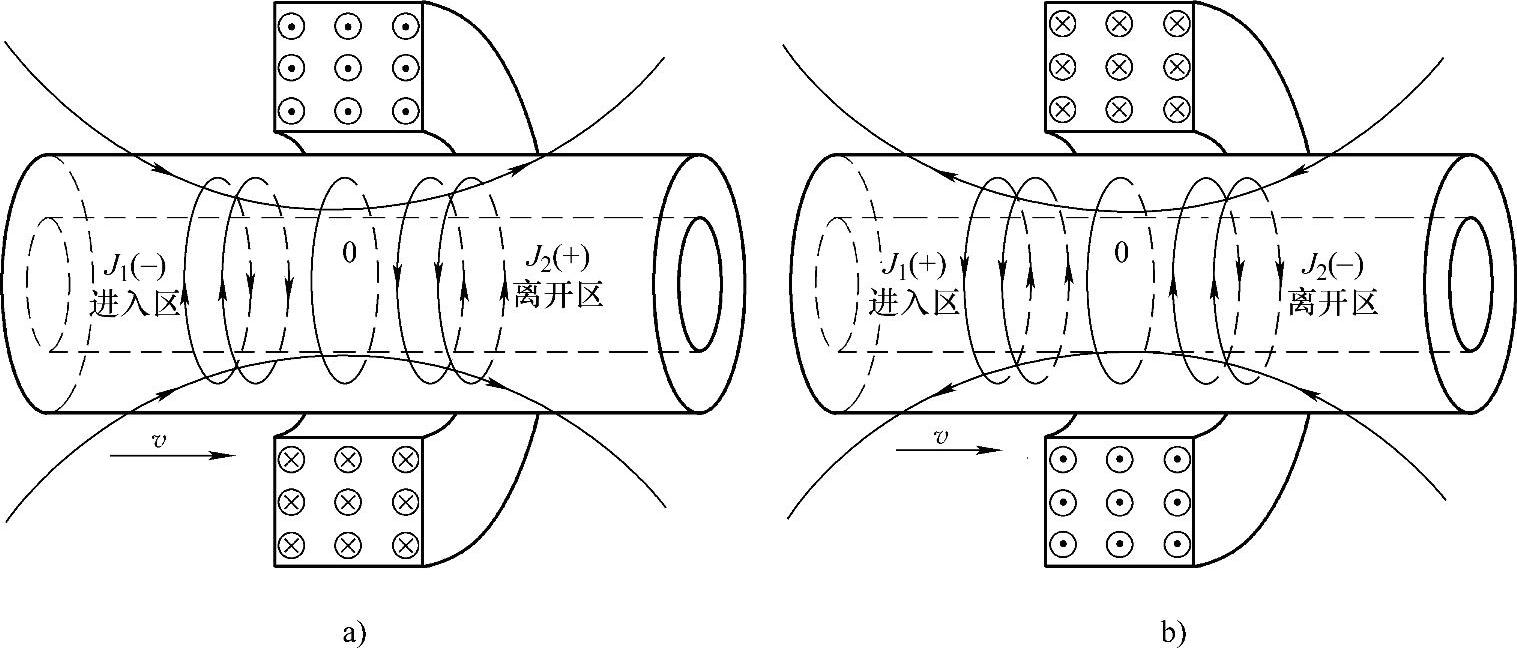
图5-2 钢管中感生涡流分布示意图

a）正方向导入磁化电流时感生涡流分布 b）反方向导入磁化电流时感生涡流分布

从图5-2中可以看出，钢管中感生电流分布方向由磁化电流方向和钢管运动方向共同决定。在进入区，钢管中的感生涡流J₁与磁化电流方向相反；在磁化线圈中间位置无感生涡流产生；在离开区，感生涡流J₂与磁化电流方向相同。从而，在感生涡流产生的磁场作用下，钢管的磁化状态将发生变化。

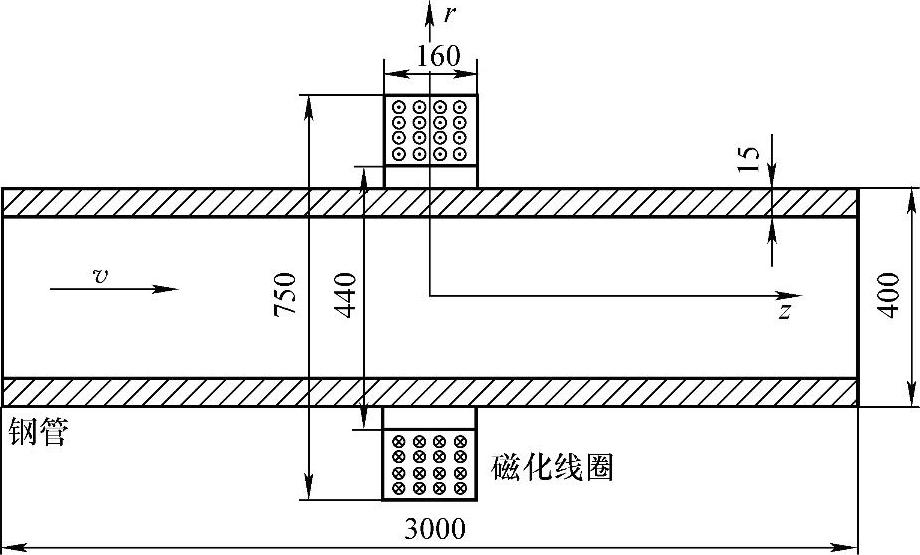
图5-3 感生涡流仿真模型几何尺寸参数

建立如图5-3所示的仿真模型。钢管直径为400mm、壁厚为15mm、长度为3000mm，材质为25钢（电导率为2×10⁶S/m）。磁化线圈内径为440mm、外径为750mm、厚度为160mm，磁化电流密度i=1.0×10⁷ A/m²，电流方向如图5-3所示。

对钢管中的感生涡流分布进行仿真研究。磁化线圈固定不动，钢管运行速度设置为1m/s，钢管从左端进入并向右端移动，当钢管中心与磁化线圈中心重合时获取感生涡流分布云图，如图5-4所示。从图中可以看出，进入区的感生涡流方向与磁化电流方向相反，离开区的感生涡流方向与磁化电流方向相同，在线圈中部感生涡流几乎为零。进入区和离开区的涡流分布相对于线圈呈对称分布，方向相反，强度基本相同，仿真结果与图5-2所示的涡流分布理论分析结论相同，其中感生涡流最大值为1.4×10⁵A/m²。

为了研究感生涡流与钢管运行速度的关系，分别取速度0.1m/s、1m/s、2m/s、5m/s、8m/s、10m/s、20m/s、30m/s、40m/s和50m/s进行仿真。当钢管中部与磁化线圈重合时提取涡流密度最大值和最小值，绘制成如图5-5所示的涡流密度与运行速度关系曲线。从图中可以看出，感生涡流与钢管运行速度成近似正比关系。钢管低速运动时感生涡流很小，可忽略不计；当运行速度增至50m/s时，涡流密度为2.01×10⁶A/m²，此时，感生涡流已接近传导电流密度。因此，高速运动时，感生涡流对钢管漏磁检测的影响不可忽视。(www.daowen.com)

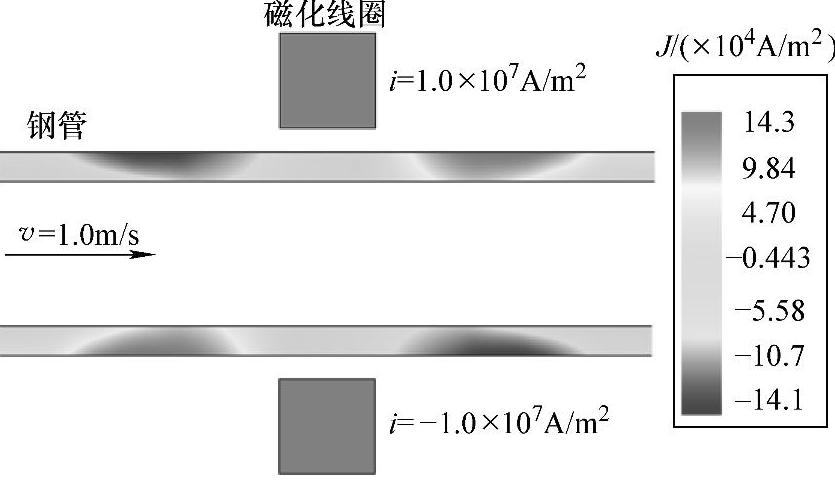
图5-4 钢管内部感生涡流分布仿真云图

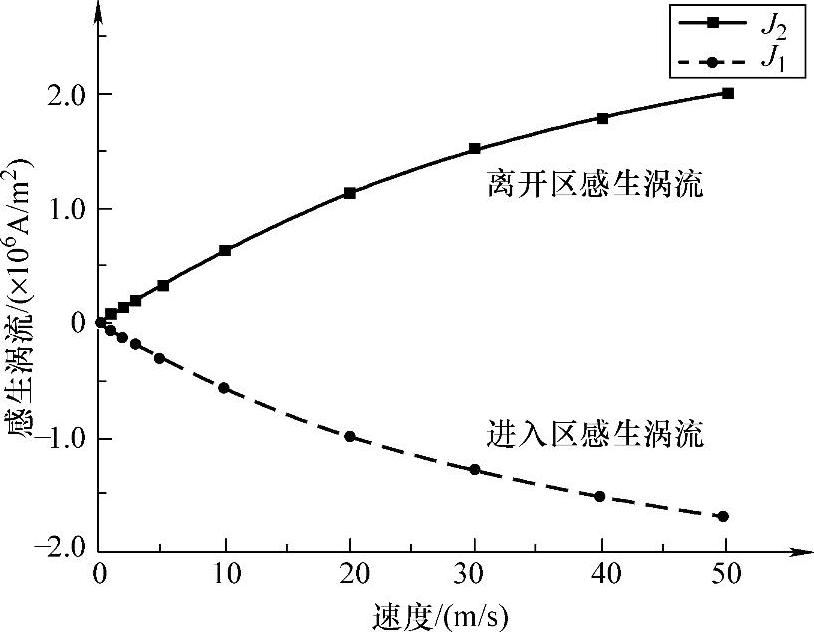
图5-5 钢管中感生涡流与运行速度关系曲线

2.磁化线圈中产生的感生电流

当钢管端部进入和离开磁化线圈时，线圈中的磁通量发生变化而产生感生电流。设磁化电源提供的电压为U₀，磁化线圈电阻为R，则磁化电源在线圈中产生的初始传导电流为I₀=U₀/R。磁化线圈通过的磁通总量为Φ，当磁化线圈中磁通总量发生变化时，根据楞次定律，线圈中将产生感生电动势U₁=-Δϕ/Δt，对应的感生电流I₁=U₁/R=-Δϕ/（ΔtR），此时，磁化线圈中通过的电流I为初始传导电流和感生电流之和，即

当线圈中没有钢管时，磁化线圈磁通总量为线圈自身产生的静态磁通量，其与磁化电流强度成正比，当磁化电流不变时，线圈磁通总量也不发生变化。此时线圈中通过的电流为磁化电源产生的初始磁化传导电流I=I₀。

当管头进入磁化线圈时，具有高磁导率的钢管磁介质进入磁化线圈内部，使得线圈内部的磁通总量增大。根据式（5-4），磁化线圈中会产生与初始磁化传导电流方向相反的感生电流，此时线圈中通过的电流为I=I₀-I₁，如图5-6a所示。

当管体通过磁化线圈时，线圈内部磁介质总量及分布特性基本不变，从而线圈内部的磁通总量也保持恒定。根据式（5-4），磁化线圈基本无感生电流产生，此时，磁化线圈中通过的电流与无钢管时相同，为磁化电源产生的初始磁化传导电流I=I₀，如图5-6b所示。

当管尾离开磁化线圈时，由于线圈内部的高磁导率磁介质不断减少，导致磁化线圈的磁通总量也不断减少。根据式（5-4），磁化线圈中会产生与初始磁化传导电流方向相同的感生电流，此时线圈中通过的电流为I=I₀+I₁，如图5-6c所示。

钢管内的磁场包括：磁化线圈通过电流I产生的磁场和钢管中感生涡流J形成的磁场。磁化线圈的磁通总量包含了由感生涡流J产生的部分磁通量，因此钢管中的涡流效应会对磁化线圈中的感生电流产生一定影响。

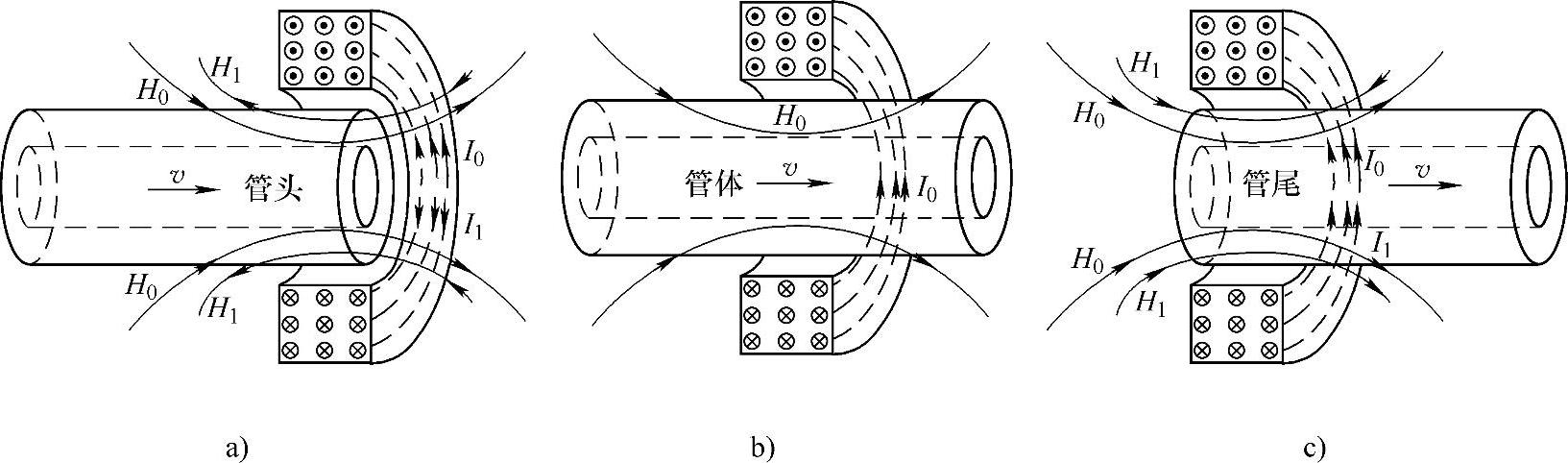
图5-6 磁化线圈感生电流分布示意图

a）管头磁化线圈感生电流 b）管体磁化线圈感生电流 c）管尾磁化线圈感生电流

采用如图5-3所示模型，进一步研究磁化线圈中产生的感生电流变化规律。其中，线圈匝数为600匝，磁化电流为5A。当钢管管头、管体和管尾分别与磁化线圈耦合时提取磁化线圈内部产生的感生电流，如图5-7所示。仿真分两种：一是考虑钢管涡流效应时分析线圈感生电流与运动速度的关系，二是忽略钢管涡流效应而单独分析线圈感生电流与钢管运动速度关系。分别取速度0.1m/s、1m/s、2m/s、5m/s、8m/s、10m/s、20m/s、30m/s、40m/s和50m/s进行仿真，获得如图5-8所示的磁化线圈感生电流与运动速度关系曲线。其中I_1cs、I_2cs和I_3cs分别为考虑钢管涡流效应时在管头、管体和管尾处线圈中产生的感生电流，I_1c、I_2c和I_3c分别为忽略钢管涡流效应时磁化线圈中产生的感生电流。

图5-8所示的仿真结果与图5-6所示的理论分析结论相同：当管头进入磁化线圈时，线圈中产生的感生电流幅值为负，即与磁化电流方向相反；当管体通过磁化线圈时，线圈中基本无感生电流产生；随着管尾离开磁化线圈，此时线圈中产生与磁化电流方向相同的感生电流。根据楞次定律，线圈中产生的感生电流会阻碍线圈磁通量的变化：当管头进入磁化线圈时，线圈中会产生反向感生电流来阻碍磁通量的增大；当管体与磁化线圈耦合时，由于线圈磁通量基本不变而无感生电流产生；当管尾离开磁化线圈时，线圈中会产生同向感生电流来阻碍磁通量的减小。

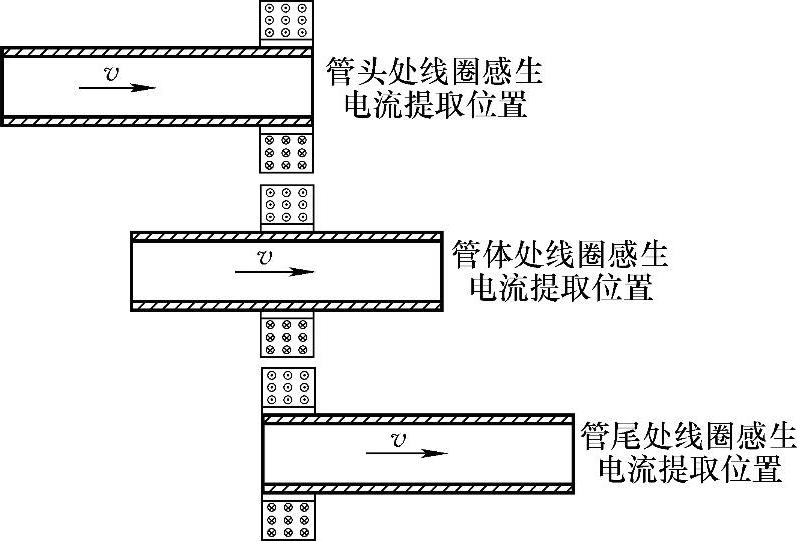
图5-7 磁化线圈感生电流仿真示意图

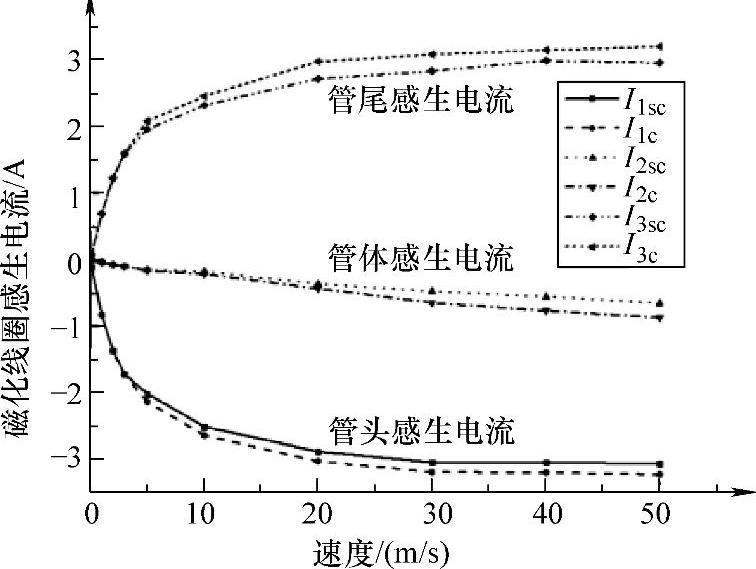
图5-8 磁化线圈感生电流与运行速度关系曲线

另外，从图5-8中可以看出，在运行速度较低时，磁化线圈中感生电流随着速度的增加而快速上升；当速度达到一定幅值时，磁化线圈中的感生电流基本保持不变。因为感生电流只能减缓磁化线圈磁通量的变化速度，而不能改变磁通量的变化趋势。

从图5-8中还可以看出，钢管中的涡流会削弱磁化线圈中产生的感生电流，即

根据楞次定律，钢管中的涡流同样会阻碍钢管中磁通量的变化。当钢管进入和离开磁化线圈时，钢管中的磁通量变化规律同样先增大后减小。由于磁化线圈磁通总量包含了钢管磁通量，所以，感生涡流在阻碍钢管磁通量变化的同时也阻碍了线圈磁通量的变化速率，最终削弱了线圈感生电流的强度。