径向剪切干涉法是一种激光干涉测量方法，即波前错位干涉，基本原理是在待测波前与其自身在空间产生的错位波前的重叠区域内，待测波前与其自身错位波前发生干涉，在重叠区域形成一组干涉条纹，通过对干涉条纹图的图像处理后得到待测波前信息。该测试方法无须单独引入参考理想平面，仅通过对干涉图的图像进行复原即可获得待测波前的相位分布。与传统的测量方法相比，该方法的优点在于光路抗振性好，系统稳定，较适合于现场测试。

在经典的径向剪切干涉仪的基础上，增加一个反射镜，使光路得到优化，便于光路的调节和降低系统误差。具体的测量系统光路详见图7.3。这种光路由一个分束棱镜、三个反射镜以及一个开普勒望远系统构成。望远系统由两个凸透镜组成，两个透镜分别位于四边形光路的两个相对支路中（任意一对支路都可）。设两个凸透镜的焦距分别是f1和f2，它们的比值M称为径向剪切比，即M＝f1／f2＜1。入射光束经分束镜后分成两路，反射光（用虚线表示）经凸透镜1后由反射镜1和2反射，由凸透镜2将光束扩束1／M倍，再经反射镜3和分束镜反射后出射；透射光（用实线表示）经反射镜3射入凸透镜1，再与经反射镜2和1反射进凸透镜1得到的缩束光束发生干涉，在光斑重叠区域内产生剪切干涉条纹，此干涉图经光阑后由面阵CCD相机采集。为了得到对比度较为鲜明的干涉条纹图，径向剪切比的平方应接近于1，即M 2→1，缩束光束和扩束光束的光强近似相等，此时干涉图的对比度最大。

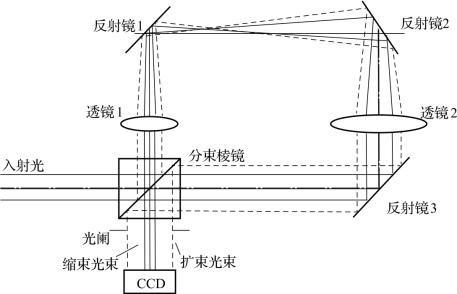
图7.3　径向剪切波前相位测量方法原理

为了便于信息提取、抑制高频噪声，通常把干涉条纹图调制到载波上。一般情况下，采用将分束棱镜旋转一定的角度对干涉图增加线性调制的方法来实现。这种方法对透射光的传播方向没有影响，但会导致反射光发生偏转，使得入射光经过光路后相对于透射光产生倾斜。用CCD相机采集干涉图信息，再利用相位恢复算法进行图像处理，从而获得待测波前的相位分布。相位恢复的

过程主要由以下两个步骤组成：

1.傅里叶变换

经过条纹去噪等预处理后，用傅里叶变换法从条纹图中提取剪切波前的相位分布。傅里叶变换法的处理过程包括以下4个步骤：

（1）对干涉条纹图的光强分布进行傅里叶变换。

调制在载波上的干涉条纹的一维光强分布可表示为

式中，a（x）和b（x）表示背景光强和条纹调制度函数；f0x表示引入的载波条纹在x方向的空间频率；φOPD（x）表示待测波前相位。则式（7.13）可以写为

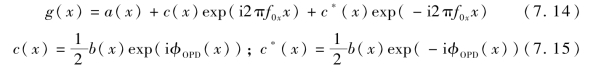
对式（7.14）进行一维傅里叶变换，可以得到

式中，C和C*分别是c（x）exp（i2πf0xx）和c*（x）exp（－i2πf0xx）的傅里叶变换，因此含有剪切波前相位信息；A（fx）是背景光强的傅里叶变换。

通过把干涉条纹调制在载波上，可以在频域中把含有重叠波前相位信息的频谱成分与背景光强分开，从而有利于相位信息的提取。所加载频越大，波前相位恢复的精度越高，但测量分辨率会降低。(www.daowen.com)

（2）频域滤波。

由于G（fx）的频谱成分C（fx－f0x）包含φOPD（x）的信息，因此只要分离出这一部分，就可以解出φOPD（x）。首先确定C（fx－f0x）在频域中的位置以及频谱宽度，然后在频域中设计中一个滤波器H（fx－f0x）滤除频谱成分C*（fx－f0x）和A（fx），即可提取出C（fx－f0x）。

（3）频谱移中处理。

C（fx－f0x）的傅里叶逆变换c（x）exp（i2πf0xx）包含载频因子f0x，因此还需把C（fx－f0x）移到频域中央以消除载频，得到c（x）的频谱C*（fx）。

（4）逆傅里叶变换。

对C*（fx）进行逆傅里叶变换得到c（x），再由式（7.15）可得剪切波前相位：

式中，Im和Re分别表示复数的虚部和实部。

根据三角函数的性质，解得的φOPD（x）被包裹到－π～π之间，因此还需要进行相位解缠运算，以得到连续的波面分布。

2.迭代求出待测波前相位

设缩束波前相位分布为φ（x），则剪切干涉波面相位分布可表示为

式中，β＝M2＜1。

由剪切波前重构待测畸变波前，需用迭代算法从式（7.18）中解出缩束波前，将缩束波前放大1／M倍即可得到待测波前。将式（7.18）左右两边的波前不断放大1／β倍，并求和抵消后得到

可以看出，当迭代次数n大到一定程度时，βn趋近于零，扩束后的波面φ（βnx）接近于平面波，可忽略，即可解出缩束波前，而φ（Mx）即待测波前。

影响波前恢复精度的因素包括剪切比、迭代次数和采样点数。因此，如何选取这些参数使得波前恢复算法精度较高，需要根据实际情况折中考虑。若用此种径向剪切干涉法测量液晶光学相控阵波前相位，由于所测波前相位分布是远场相位分布，且测得的波前相位畸变与被测件的驱动电压单元无法一一对应，因此，相位畸变溯源非常困难。