（1）流场计算方法。

流场数值计算的基本过程是在空间上采用有限体积方法或其他类似方法将计算域离散成很小的体积单元，在每个单位体积单元上对离散后的控制方程进行求解。由此可见，流场计算方法的本质是对离散后的控制方程组进行求解。对本章涉及的多相流场离散方法有很多，包括半隐式连接压力方程——SIMPLE、调和一致的SIMPLE算法——SIMPLEC和压力的隐式算子分割算法——PISO等。SIMPLE和SIMPLEC是两步算法，即一步预测、一步修正，而PISO算法增加了一个修正步，包括一步预测和两步修正，在完成第一步修正得到的流场参数后寻求二次改进值，目的使它们更好地同时满足动量方程和连续性方程。PISO算法由于采用了预测—修正—再修正的三步，加快了单步迭代中的收敛速率。PISO算法在求解瞬态问题时具有明显优势，因此被本章采用，其计算流程图如图5.2.2所示。压力项离散采用PRESTO！离散格式，对流项采用QUICK离散格式，而动量方程和耗散采用二阶迎风格式。此外，本章采用有限体积法对流场的控制方程进行离散化处理，并使用耦合算法对流场进行计算。计算过程采用双精度模式，计算模型采用适合低雷诺数的Laminar模型，近壁面层流计算采用滑移网格边界条件进行处理。同时，对流场的计算还使用了油膜运动规律的求解模型、气液两相流Mixture模型、Singhal-et-al气穴求解模型等[208]。此外，将气液相变和热量通过源项的形式添加到流体动力学控制方程中，耦合算法求解流程如图5.2.3所示。

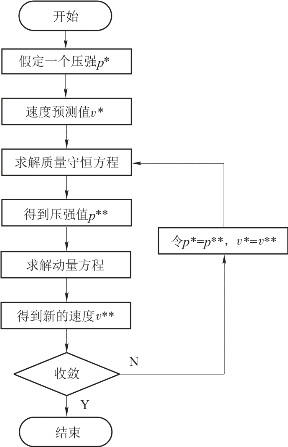
图5.2.2　PISO算法流程图

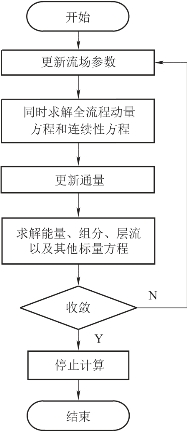
图5.2.3　耦合算法求解流程图

（2）计算收敛条件。

应用有限体积法对控制方程进行离散后，对于任意变量ϕ在计算单元p中的守恒方程为：式中，ap为单元中心系数；anb为计算相邻单元影响系数；b为源项的常数部分与边界条件引起的变量。采用耦合算法求解器时，各方程的规则化残差可以定义为：

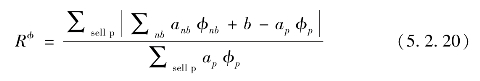
当变量ϕ计算后所得的残差小于指定收敛精度时，则认为该计算收敛，本章对计算收敛精度的要求为10-6，且进出口流量相对差小于1%。为了提高计算的准确性，考虑气穴现象对支承轴承的性能影响，特作如下假设：因为支承轴承的变形较小，所以在计算时不考虑支承轴承的变形，认为支承轴承油膜外表面是无限刚度的。润滑油通过油口进入油腔内部，经计算得Re小于2 300，油腔内部为层流状态。在稳态状态下选择操作压力为101 325 Pa，汽化压力为28 186 Pa。(www.daowen.com)

（3）模型有效性验证。

为了充分地验证该研究方法的有效性，以文献[209]中的测试轴承为对象，基于本章建立的多相流计算模型，针对不同工况下的轴承进行流体动力学仿真计算。将仿真结果与文献[209]中轴承试验结果对比，验证本书计算方法的正确性和有效性，仿真计算参数如表5.2.1所示。

表5.2.1　轴承仿真计算参数

网格密度是影响流场数值计算的一个重要因素，特别是针对复杂的工程问题，网格数量的多少直接关系到计算结果的经济性和精确性，因此开展网格密度无关性验证检验对计算效率和准确性具有重要的意义。根据上述模型建立的轴承物理模型分别建立不同密度的网格模型。采用单因素分析法保持不同工况的数值算法一致，以油膜压力最大值达到收敛时间和计算结果作为评价标准。图5.2.4为不同网格密度下计算得到的在外载为8 kN时，轴承油膜最大压力值和网格密度情况。由图可知，当网格较为稀疏时计算的油膜最大压力值较小，随着网格密度的增加，油膜最大压力值逐渐增大，并保持稳定。当径向网格层数为10时，网格数量为41万，油膜最大压力值为3.764 MPa，计算时间为1 500 s。而当径向网格层数为30时，网格数量为58万，油膜最大压力值为3.782 MPa，计算时间为3 300 s。网格数为41万和58万两种工况计算得到的油膜最大压力值相当，基本满足计算精度要求，但58万网格数模型的轴承总计算时间是41万网格数的两倍，效率较低。因此，综合考虑计算精度和计算效率，本书所有高速重载机械压力机支承轴承油膜动力学计算模型径向网格层数设定为10。

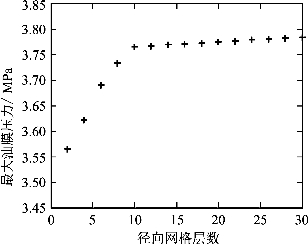
图5.2.4　轴承仿真值与试验值对比

图5.2.5给出了在不同载荷（6 kN、8 kN）作用下，油膜周向压力分布情况仿真计算结果和试验测试结果对比曲线。由图中可以看出，仿真计算得到的压力峰值略高于实测值，出现偏差的原因是忽略了润滑油的惯性力，其中还存在计算参数偏差、测量误差等因素影响。但仿真结果与试验结果相差很小，整体压力分布吻合度较好，这表明本章所提出的多相流计算方法能有效地进行支承轴承动力学性能分析。

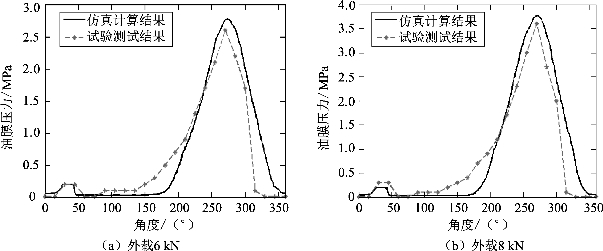
图5.2.5　轴承仿真值与试验值对比