5.2.3.1　气穴方程

在支承轴承运转过程中，润滑油的油膜会产生两个区域（收敛区和发散区）。收敛区内充满在一定压缩作用下产生正压力的润滑油，而发散区域内的油膜压力为非正值，这将导致该区域油膜破裂，从而发生气穴现象。由文献[199]测试试验结果可以看出，当润滑油流经发散区域时，由于气穴现象的存在润滑油不能连续流动，从而该区域成为液体与气体共存的两相流状态。当油压为饱和蒸气压力值时，两相润滑油的相互转化达到动态平衡，各相成分值处于稳定值，气穴方程表达式如下：

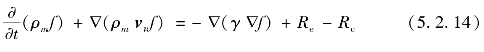
其中，

式中，ρm为润滑油混合物平均密度；vv为气体速度矢量；f是气相质量分数；γ是交换系数；Re和Rc分别为气穴的生产率和凝聚率。

5.2.3.2　气液多相流模型

气穴现象的存在会破坏油膜的连续性，常用的雷诺边界条件适用于油膜破裂边界条件，但对油膜再形成状态的计算却无法准确求解[200-201]。因此，有必要对油膜破裂边界条件进行分析，这将有助于提高计算的准确性。

针对上述存在的问题，国内外学者对此做了大量的研究工作[202-203]。破裂边界条件主要包括Sommerfeld、Half-Sommerfeld和Reynold三种形式，如图5.2.1所示。不同的边界条件会产生不同的压力轮廓曲线，为了准确模拟气穴区域的流场状态，本节对以下三种边界条件进行详细的分析。如图5.2.1（a）所示，Sommerfeld模型假设流体可以承受很高的张力，即允许其值低于周围环境压力，甚至负压。有相关试验验证了某些流体在特定条件下可以满足上述情况，但对于本章研究的支承轴承与实际情况不符。由于润滑油的流动不仅会产生很大的剪应力，油膜分子还可能会更容易形成低于相邻油膜的油压，从而导致油膜的破裂。而Sommerfeld模型中周向压力分布是反对称周期性连续函数，忽略了油膜在发散区内足够大的负压条件下发散破裂的现象，与实际情况不符。Dowson等[204]对Sommerfeld模型做了相应的改进。由图5.2.1（b）可以看出，Half-Sommerfeld模型中假设当油膜发散区内低于破裂压力时，其发散区内压力全部为零，相对Sommerfeld模型更符合实际情况。但Half-Sommerfeld模型忽略了当油膜再次形成时，收敛区与发散区的过渡处出现流体流动的不连续性，此外也不满足质量守恒定律。在此基础上，Mahdavi等[205]提出的Reynold模型假设全油膜内不允许低于气穴压力的存在，同时在气穴区内压力保持不变，满足流体流动的连续性。相对于其他两种边界条件，Reynold边界条件准确性较高，也更为接近于实际情况。(www.daowen.com)

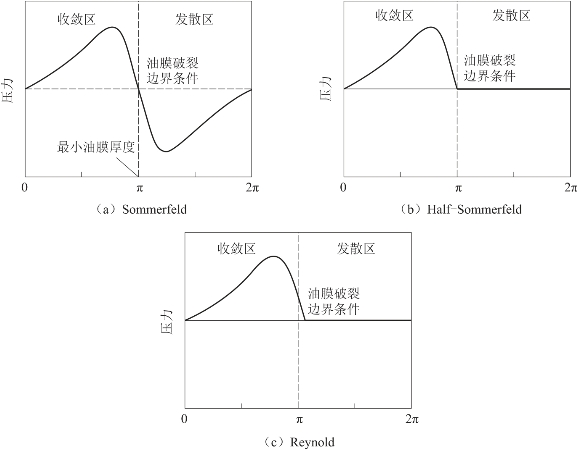
图5.2.1　滑动轴承不同油膜破裂边界条件的压力分布

针对支承轴承负压区的气液两相流混合存在现象，本节基于Mixture模型建立了高速重载机械压力机曲轴支承轴承的三维CFD两相流计算模型。Mixture模型适用于流体中混合相或分散相的体积分数超过10%的情况。支承轴承的汽化区域内大部分气体体积分数都超过10%，甚至部分气穴体积分数接近100%，因此采用基于Mixture建立的两相流模型计算更符合实际情况[206-207]。两相流混合模型的求解必须在混合相的连续性方程、质量守恒方程以及动量守恒方程下进行。气液多相流模型控制方程的表达式如下：

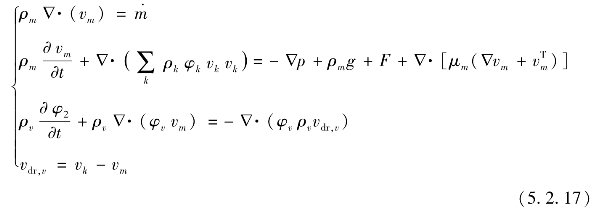
式中，k和m下标分别表示第k相和混合物平均值；m　˙为两相直接的质量传递；μm为混合黏度；φk为体积分数；νm为混合体平均速度；νdr，v是第k相的漂移速度。

两相流模型的计算边界条件为：

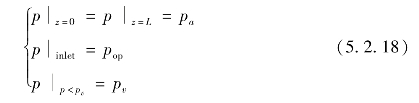
式中，pa为环境压力；pv为汽化压力；下标op表示供油区压力。