5.2.2.1　质量守恒方程

在进行计算流体动力学分析时，首先将流体区域划分为有限个流体微团，再对每一个微团进行分析[195]，将润滑油视为不可压缩流体，流场中各流体微团均须满足连续性条件，即连续方程：

引入矢量符号，式（5.2.1）表达式为：

引入矢量符号，式（5.2.1）表达式为：

式中，ρ为润滑油密度；t为时间；∇为哈密顿算子；u、v和w为流体运动速度矢量（v）在x、y和z方向的分量。

式（5.2.1）和式（5.2.2）表示质量方程的流体为瞬态可压缩流体，由于本章所研究的油膜区域流体流动状态处于稳态均质不可压缩，则密度ρ为常数，故质量方程表达式可改写成：

式中，ρ为润滑油密度；t为时间；∇为哈密顿算子；u、v和w为流体运动速度矢量（v）在x、y和z方向的分量。

式（5.2.1）和式（5.2.2）表示质量方程的流体为瞬态可压缩流体，由于本章所研究的油膜区域流体流动状态处于稳态均质不可压缩，则密度ρ为常数，故质量方程表达式可改写成：

5.2.2.2　动量守恒方程

除了满足质量守恒方程之外，润滑油运动同时也应该满足动量守恒方程[196-197]。动量守恒定律实际上也是牛顿第二定律，根据该定律可推导出x、y和z三个方向的动量守恒方程表达式为：

5.2.2.2　动量守恒方程

除了满足质量守恒方程之外，润滑油运动同时也应该满足动量守恒方程[196-197]。动量守恒定律实际上也是牛顿第二定律，根据该定律可推导出x、y和z三个方向的动量守恒方程表达式为：

当黏度为常数时，不随坐标位置而变化条件下的矢量形式可以写成：

当黏度为常数时，不随坐标位置而变化条件下的矢量形式可以写成：

由于流体区域内为不可压缩流体，其密度和黏性系数为常数时，动量方程表达式为：(www.daowen.com)

由于流体区域内为不可压缩流体，其密度和黏性系数为常数时，动量方程表达式为：

式中，F为微元体的质量力；p为流体微元上的压力；μ为黏度系数；λ为第二分子黏度（λ=-2/3）。

5.2.2.3　能量守恒方程

假设润滑油的动力黏度沿油膜厚度方向不变，且润滑油密度与温度无关，则热流体动压润滑除了满足以上两个方程之外，同时也应该满足能量守恒方程[198]，能量守恒方程与轴承热传导方程如下：

式中，F为微元体的质量力；p为流体微元上的压力；μ为黏度系数；λ为第二分子黏度（λ=-2/3）。

5.2.2.3　能量守恒方程

假设润滑油的动力黏度沿油膜厚度方向不变，且润滑油密度与温度无关，则热流体动压润滑除了满足以上两个方程之外，同时也应该满足能量守恒方程[198]，能量守恒方程与轴承热传导方程如下：

式中，ρ为油膜密度；k为油膜导热系数；u、v和w分别为油膜x、y、z方向的速度分量；r为径向坐标；T为油膜温度。边界条件为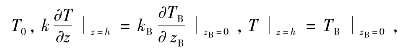其中θ为周向转角；kB为轴承导热系数；TB为轴承的温度；zB为轴承的厚度。

由于本章研究的流体为黏性流体，即该状态方程对理想气体有：

式中，ρ为油膜密度；k为油膜导热系数；u、v和w分别为油膜x、y、z方向的速度分量；r为径向坐标；T为油膜温度。边界条件为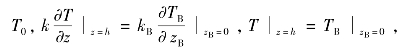其中θ为周向转角；kB为轴承导热系数；TB为轴承的温度；zB为轴承的厚度。

由于本章研究的流体为黏性流体，即该状态方程对理想气体有：

式中，R为理想气体常数。

式中，R为理想气体常数。