含间隙多体系统动力学建模的关键是建立转动副间隙与机构之间的运动学关系。为了更有效地描述含柔性构件高速重载机械压力机传动机构运动过程，将图4.1.1所示的含间隙转动副模型引入多体系统的动力学模型中，并通过轴承中心与轴中心的相对位置变化来表示转动副元素之间的运动关系[167-168]。同时，还可以通过相对位置的大小来反映碰撞体间的变形大小。

式中，x和y分别表示轴承与轴之间水平和垂直方向的距离；当h＞0时，表示轴承与轴处于分离状态，而h≤0时，则表示轴承与轴之间发生了接触。

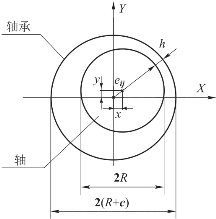
图4.1.1　含间隙转动副模型示意图

对于理想机构而言，通常认为轴承与轴是同心的，且相互之间不发生碰撞。但是在实际的机构运行过程中，由于转动副间隙的存在，轴承与轴之间会产生相对运动，从而产生偏心距eij。由于转动副间隙会对传动机构动力学特性产生较大的影响，因此基于上述转动副间隙模型进行建模，轴承与轴之间的间隙大小可以表示为：

式中，RB与RJ分别表示轴承与轴的半径。

多体系统中转动副间隙模型如图4.1.2所示，体i（轴承）和体j（轴）的质心位置分别由Oi和Oj表示[169]。Pi和Pj分别表示轴承和轴的中心位置，轴承与轴的间隙矢量为：

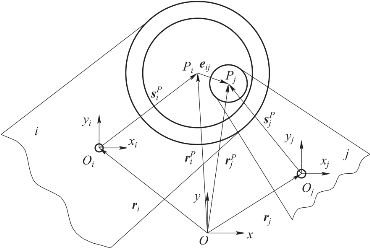
图4.1.2　多体系统中转动副间隙模型

式中，全局惯性坐标系下表示的位置矢量和通过坐标变换[170]，在体坐标系下可表示为：

由图4.1.1可知，间隙矢量的偏心距可表示为：

轴承和轴碰撞时的法向单位矢量表达式如下：(www.daowen.com)

如图4.1.3所示，由接触碰撞引起的接触变形可以写成：

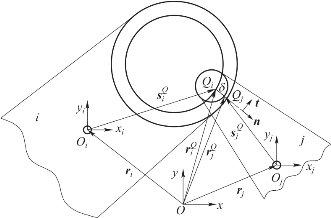
图4.1.3　碰撞时转动副间隙示意图

式中，轴承与轴半径差c为常数。

轴承和轴上的接触碰撞点Qi和Qj的位置由下式决定：

式中，Ri和Rj分别为轴承和轴的半径。

考虑接触碰撞过程的能量损耗是计算碰撞问题不可缺少的因素，接触碰撞点Qi和Qj的速度可由式（4.1.9）和式（4.1.10）求导得到：

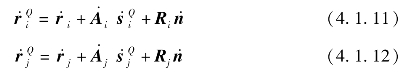
碰撞点位置的相对法向速度和相对切向速度在平面上的投影，如图4.1.4所示。

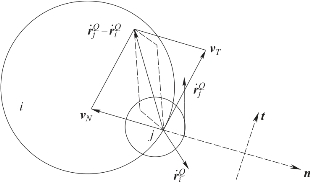
图4.1.4　轴承与轴碰撞点的速度矢量

从图4.1.4可知，通过法向速度可以判断接触体之间的状态，即接触或分离。而接触体间是滑动状态还是黏滞状态可由法向速度决定，则相对速度标量表达式如下：

式中，切向单位矢量t可由法向单位矢量n逆时针旋转90°得到。