转动副间隙的存在一定会引起轴承与轴之间产生摩擦现象，摩擦力对含间隙传动机构的动力学特性会产生一定的影响。因此，在含间隙传动机构动力学建模过程中，转动副元素之间的摩擦力影响不能忽略。由于本章研究不考虑润滑，故转动副间摩擦力为干摩擦情况。

Coulomb摩擦力模型在摩擦问题上应用最为广泛[163]，该模型认为摩擦力与作用在摩擦面上的正压力成正比，与接触面积无关，其表达式为：

式中，μd为滑动摩擦系数。

由式（3.2.14）可以看出，Coulomb摩擦模型没有考虑接触碰撞过程与切向速度的关系，该摩擦力模型无法根据不同的摩擦状态进行相应的转换。

针对上述存在的问题，国内外学者做了大量的研究工作[164-166]。Dubowsky和Rooney分别对Coulomb摩擦模型做了相应的改进，主要是为了解决在接触碰撞时切向速度为零情况下，如何使摩擦力连续并能有效处理摩擦状态转换的问题。最初，Dubowsky认为碰撞时切向摩擦力是一个方向与切向速度相反的常力，该摩擦力模型可以定性地反映摩擦力与切向速度之间的关系，其摩擦力与切向速度之间的映射关系如图3.2.12所示。

图3.2.12　摩擦力模型

进一步，Rooney和Deravi提出了一种模型，采用一组方程来计算切向摩擦力。在该摩擦力模型中，当接触碰撞过程相对切向速度不趋向于零时，也即相对切向速度不为零时，摩擦力可以表示为：

式中，μf表示滑动摩擦系数。

而当相对切向速度趋于零时，摩擦力可以表示为一个不等式：(www.daowen.com)

由图3.2.12可以看出，当相对切向速度为零时，由表中Coulomb摩擦力改进模型计算得到的摩擦力直接由-Ft跃变到Ft，并没有考虑相对速度为零的情况，由于这个过程是瞬间完成的，因此这种计算方法对于数值积分计算时很难求解。然而，Rooney提出的另外一种摩擦力模型虽然消除了由于摩擦力瞬间转变带来的问题，但还是没能给出当切向速度接近于0时，摩擦力数值的表达式。

基于Coulomb摩擦力模型，Threlfall提出了一种改进的摩擦力模型，在该摩擦力模型中，当摩擦力由-Ft跃变到Ft的过程中，即当相对切向速度趋于零时，摩擦力可以表示为：

式（3.2.17）中νt为比νr小的在切向速度趋向于零时的特征速度，是一个特点参数。当νr的取值比较小时，摩擦力模型就与Dubowsky提出的模型一致。当νr取值比较适中时，便可以使摩擦力曲线光滑，摩擦力模型如图3.2.13（a）所示。该模型在使用过程中需要人为设定一个适合的νr值，而νr值的选取缺少标准准则，这会引起摩擦力描述的误差，其计算精度较低。

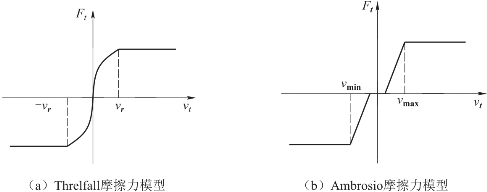
图3.2.13　改进的摩擦力模型

在此基础上，Ambrosio将动态修正系数cd引入摩擦力模型中，提出了一种改进的摩擦力模型，如图3.2.13（b）所示。在该模型中，摩擦力不仅与滑动摩擦系数有关，还与动态修正系数cd有关，是一种动态摩擦力，其表达式可以写为：

式中，cd为动态修正系数。其中cd的表达式如下：

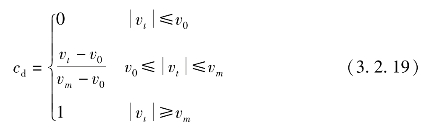
式中，v0和vm为给定的速度极限值。