3.2.1.1　Kelvin-Voigt线性弹簧阻尼模型

对于两个球体接触碰撞问题，Kelvin-Voigt模型用一组线性平行弹簧-阻尼器描述接触变形过程[89，158]。如图3.2.3所示，弹簧可以描述接触体的弹性变形，阻尼器可以描述碰撞中动能的损失，模型假设弹簧和阻尼器均为线性已知常数。

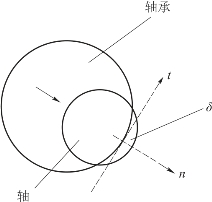
图3.2.2　含间隙转动副接触碰撞示意图

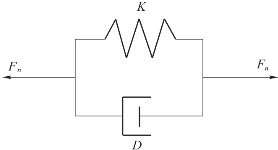
图3.2.3　Kelvin-Voigt线性弹簧阻尼模型

Kelvin-Voigt法向接触力表达式如下：

式中，K为弹簧刚度系数；b为阻尼系数；δ为在碰撞方向上碰撞体相对挤压深度。取K=6.61×1010，b=2 000 N˙s/m，仿真结果如图3.2.4所示。

由图3.2.4可知，接触力大小与变形深度为线性关系，该模型优点在于简单方便。但是模型存在一定的局限性，主要体现在接触力在初始时不连续，弹性力和阻尼力由零时刻随时间增长。当碰撞体分离时变形量为零，相对速度可能会出现负值，即弹性力和阻尼力之和也可能小于零，这与实际情况不符。此外，接触力与碰撞体材料属性、接触面形状等因素有关，简单的线性关系也是不准确的。因此，该模型不能准确地描述接触碰撞过程，误差较大。

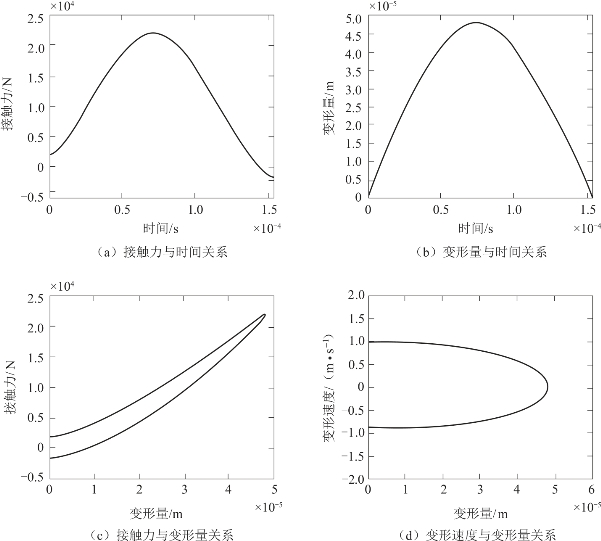
图3.2.4　Kelvin-Voigt接触模型仿真结果

3.2.1.2　Hertz非线性弹簧模型

Hertz[159]在研究弹性非协调接触时提出了Hertz接触理论，Hertz接触碰撞力模型是基于完全弹性变形，并假设接触表面光滑。Hertz接触力表达式如下：

式中，n为接触指数，取n=1.5；其他各项含义与前文定义相同。

其中，两球体接触碰撞刚度系数表达式为：

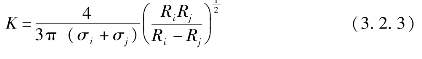
材料参数σi和σj可由下式求得：

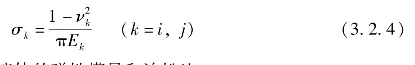
式中，Ek和νk分别为碰撞体的弹性模量和泊松比。

由图3.2.5可以看出，接触力与变形量之间是非线性关系，但是还可以发现Hertz接触碰撞力模型是基于纯弹性理论，没有考虑接触碰撞过程中能量的损耗。因此，加载过程存储的接触能量与卸载过程中的恢复能量正好相等。虽然Hertz接触碰撞力模型不能反映含间隙转动副接触碰撞过程中的能量损失，但相比Kelvin-Voigt线性接触碰撞模型，该模型可以较好地描述坚硬材料或低速接触碰撞过程。

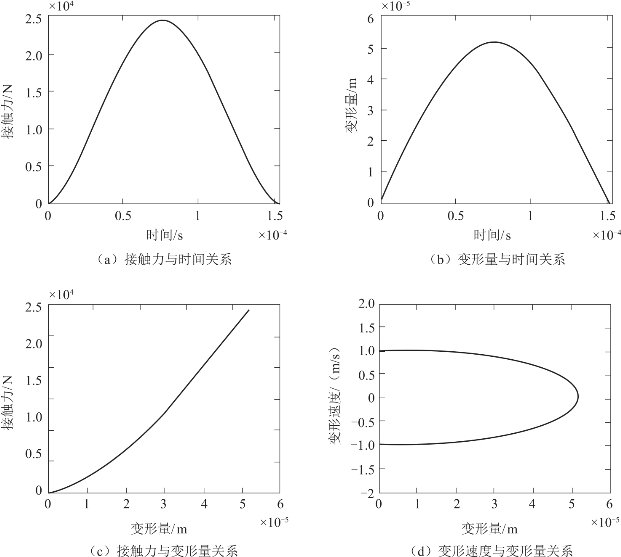
图3.2.5　Hertz接触模型仿真结果

3.2.1.3　Hunt-Crossley非线性弹簧阻尼模型

连续接触碰撞力模型是一种以弹簧阻尼系统代替接触区复杂变形的近似方法，而且模型中必须包含轴与轴承接触碰撞过程中的能量损失。接触碰撞过程的能量损失是一定存在的，而且不能被忽略。由上述分析可知，虽然Hertz接触碰撞力模型没有考虑接触碰撞过程中的能量损耗，但该模型可以较好地描述非协调接触碰撞过程。Hunt和Crossley基于Hertz接触碰撞力模型，并克服Kelvin-Voigt线性弹簧阻尼的局限性，提出了一种考虑接触碰撞过程中的能量损失的非线性弹簧阻尼模型[160]。该模型的接触力计算公式为：

(www.daowen.com)

式中，阻尼系数b与恢复系数ce有关，对于中心碰撞问题，取α=2b/3K，恢复系数为0.9。

由仿真结果（图3.2.6）可知，Hunt-Crossley接触碰撞力模型考虑了材料属性对接触碰撞过程的影响，初始接触和分离点接触力没有出现不连续情况。该模型可以有效地描述接触碰撞过程的能量损耗，并且接触力和变形量之间为非线性关系。

3.2.1.4　Lankarani-Nikravesh非线性弹簧阻尼模型

Lankarani和Nikravesh在Hunt-Crossley接触碰撞模型研究的基础上，假设含间隙传动机构接触碰撞过程中的能量损失是由材料阻尼引起的，并且含间隙转动副中轴与轴承为低速碰撞，提出了另一种非线性弹簧阻尼模型[92，161]，基于上述假设条件建立了一种新的接触力模型，其表达式如下：

式中，D为碰撞过程中的非线性阻尼系数，可以表示为：

式中，η为滞后阻尼因子。假设能量损失是由材料阻尼引起的，考虑滞后阻尼的碰撞力曲线如图3.2.7所示。

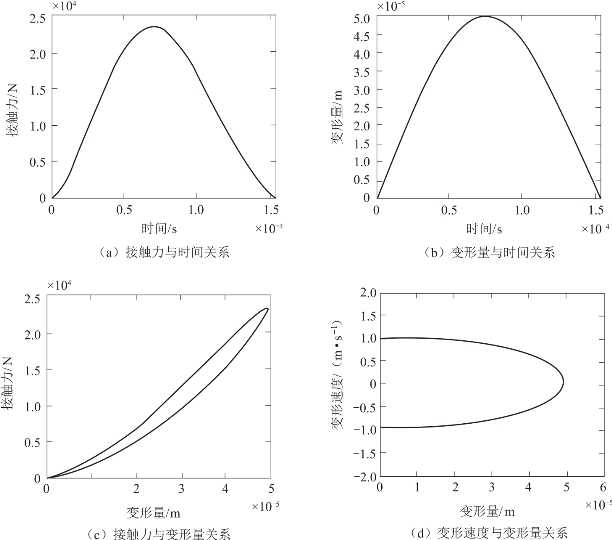
图3.2.6　Hunt-Crossley接触模型仿真结果

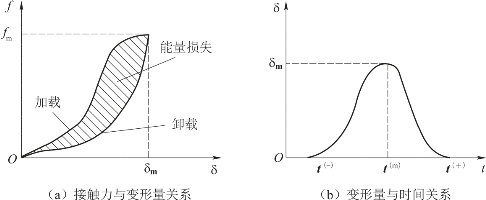
图3.2.7　考虑滞后阻尼的碰撞力曲线

图3.2.7中，t（-）、t（m）和t（＋）分别为初始碰撞时刻、达到最大变形量时刻和碰撞体分离时刻。最大变形量δm和接触力fm与达到最大变形量时刻相关。式（3.2.6）中阻尼系数和滞后阻尼因子可根据能量守恒定理和冲量定理求得[162]。碰撞前后的能量将以热的形式损耗，基于恢复系数ce，能量损耗计算公式为：

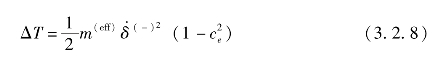
其中，

式（3.2.8）可以由接触力沿黏滞环的环路积分得到：

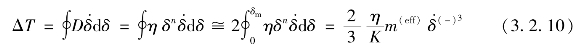
结合式（3.2.8）和式（3.2.10）可得滞后阻尼因子为：

式中，为初始碰撞速度；其他各项含义与前文相同。

将式（3.2.11）代入式（3.2.6）中可得：

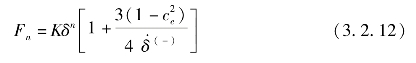
由于Lankarani和Nikravesh提出的非线性弹簧阻尼接触碰撞力模型能够反映接触碰撞过程中碰撞体的能量损失行为，并且全面地包含了碰撞体材料属性、局部变形、碰撞速度等信息，因此被国内外学者广泛地应用于含间隙机构动力学特性的研究中，Lankarani-Nikravesh接触碰撞力模型仿真结果如图3.2.8所示。

由图3.2.8计算结果可知，Lankarani-Nikravesh接触碰撞力模型考虑了初始碰撞速度对于接触碰撞过程的影响，不仅能够描述接触碰撞过程中的能量损耗情况，还能反映阻尼滞后的特性，更接近实际情况地表达了转动副间隙的接触碰撞过程。此外，Lankarani-Nikravesh接触碰撞力模型是一种以弹簧阻尼系统代替接触区复杂变形的近似方法，而且模型中包含了轴与轴承接触膨胀过程中的能量损失。

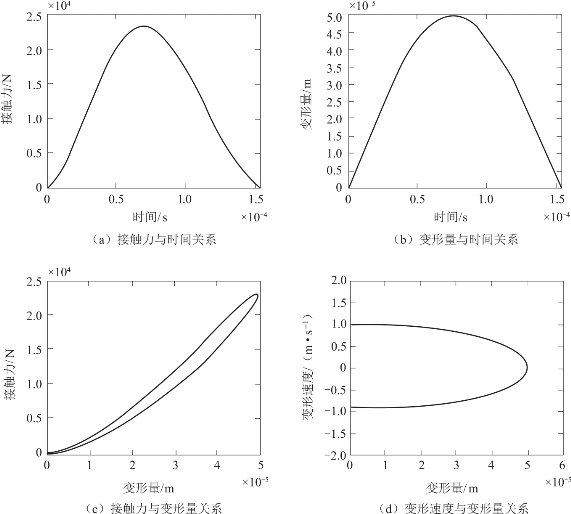
图3.2.8　Lankarani-Nikravesh接触模型仿真结果