为了提高机构（或构件）的刚度及承载能力等动力学特性，往往会附加一些不影响原机构运动规律和自由度的构件或机构。由于机构中存在理论过约束，各构件变形之间存在耦合，机构的动力学建模就变得更加复杂。目前，高速重载机械压力机传动机构曲轴支承系统较为复杂，对此类重载过约束构件动力学建模的相关研究较少，设计理论不够完善，动力学模型计算烦琐，极易出错。因此，本章对如何寻找合适的过约束曲轴支承系统动力学建模方法进行计算与分析。

由图2.4.1可以看出，曲轴受到轴承支承力、连杆作用力和平衡连杆作用力的影响。根据受力分析可以列出2个平衡方程，由于曲轴有6点支承，包含有6个未知量。因此，无法通过2个平衡方程求解出所有的未知量，在材料力学中将这类问题归纳为超静定问题[137-138]。在工程中，为了提高结构刚度，经常会在静定机构上增加构件引起额外的约束。该原理结构出于安全性设计以及提升曲轴抗偏载能力的考虑，在静定结构中添加了额外构件导致过约束。

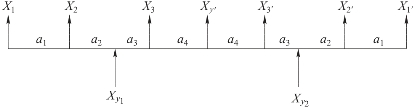
图2.4.1　曲轴受力图

针对这类问题，通常可以采用力法或位移法建立超静定结构的变形协调方程，以此作为补充方程将超静定问题转化成静定问题进行计算。在计算超静定结构的反力和内力时，不仅要考虑静力平衡条件，还必须考虑位移约束条件。力法是以多余未知力作为基本未知量，以静定结构计算为基础，通过位移约束条件建立力法方程求解出多余未知力，从而把超静定结构计算问题转化为静定结构计算问题[139]。根据本节研究的曲轴受力形式分析，可以采用力法建立变形协调方程直接作为补充方程，简化后的曲轴受力图如图2.4.2所示，力法方程的通用形式为：

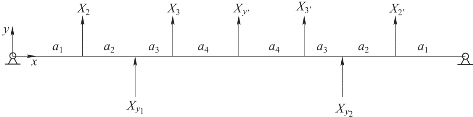
图2.4.2　简化后的曲轴受力图

式中，Xi为未知力；δi表示Xi单独作用于基本结构时引起点i沿X方向上的位移；Δi为载荷引起基本结构沿X方向上的位移。

补充方程的形式为扰度曲线方程，其表达式为：

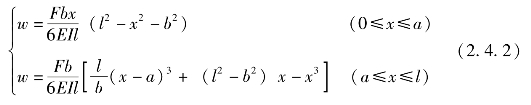
式中，l为梁的长度；x为力F作用点位置；a和b分别为作用点距梁左右两端的距离；E为弹性模量；I为惯性矩。

其惯性矩表达式为：

式中，d为轴的直径。(www.daowen.com)

根据结构的对称性可知，X1=X1′，X2=X2′，X3=X3′，联立式（2.4.1）～式（2.4.3）可得曲轴的力学方程表达式为：

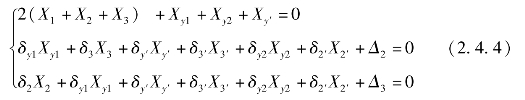
根据上述理论分析，从结构力学方面入手，完成对曲轴的承载能力分析，仿真计算参数如表2.4.1所示。在最大载荷工况下，忽略摩擦力的影响，进行曲轴的结构力学仿真，计算结果如表2.4.2和图2.4.3所示。

表2.4.1　曲轴承载能力仿真计算参数

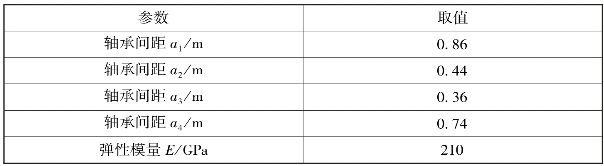
表2.4.2　曲轴受力分布计算结果

续表

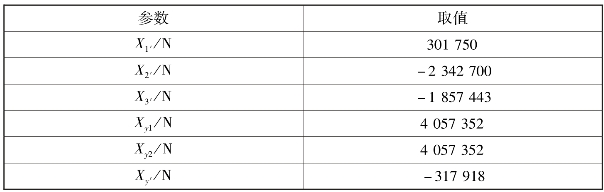
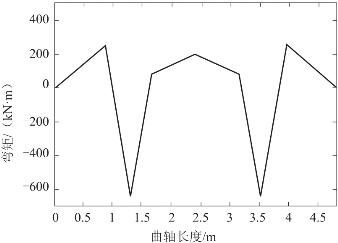
图2.4.3　曲轴弯矩计算结果

根据曲轴材料（45钢）的屈服极限，结合上述载荷分析结果，可以得到曲轴各部分的最小截面尺寸，如表2.4.3所示。

表2.4.3　曲轴各部分最小截面尺寸

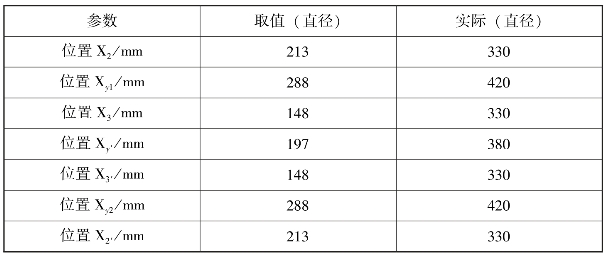
在上述计算过程中，综合考虑惯性载荷与冲击作用，并与实际的加工尺寸对比可知，安全系数的计算结果均在1.45以上，完全满足设计要求。