达朗贝尔原理（D'Alembert principle）阐明，对于任意机械系统中的构件，所有惯性力和施加的外力经过符合约束条件的虚位移，所做虚功的总和等于零。由凯恩方程可知，作用于构件的广义主动力与广义惯性力之和等于零。由此可知，作用于构件的外力与动力的反作用力之和等于零。达朗贝尔原理是分析动力学的基础，具有深刻的意义。从数学角度看，达朗贝尔原理是牛顿第二运动定律的移项，但其主要的贡献在于通过加惯性力的办法将动力学问题转化为静力学问题处理，即将平面静力分析方法应用于刚体的平面动力学分析，极大地简化了动力学问题的复杂程度，且求解过程中充分使用了静力学分析的各种求解技巧，因此该方法被广泛应用于工程实际中。

在冲压设备速度很低的时代，把传动机构作为一个静力系统，只进行静力分析即可满足要求。随着冲压设备速度的提高，构件的惯性力不能再被忽略。根据达朗贝尔原理，可将惯性力计入静力平衡方程来求出为平衡静载荷和动载荷而需在驱动构件上施加的输入力或力矩，以及各运动副中的反作用力，这样一种分析方法被称为动态静力学分析。

由此可见，对于运行速度较低的机械压力机，仅对传动机构进行静力学分析就可以满足设计要求。由于高速重载机械压力机具有转速高和吨位大的特点，传动机构中各构件惯性力也随之增大，其影响不容忽视。因此，考虑高速重载机械压力机在运动过程中受惯性力的影响，基于达朗贝尔原理对压力机的构件进行动态静力学分析[30，135-136]。如图2.3.1（a）所示，假设一个平面机构由n个运动构件组成，运动构件之间由移动副或转动副相互连接，且至少有1个运动构件与固定机身相连接。

图2.3.1　任意平面连杆机构动力学分析

根据达朗贝尔原理，可将机构拆分为相互独立的分离体（构件），如图2.3.1（b）所示。对于任意构件i，在不考虑摩擦时，将构件i上的所有外力/力矩向固定在构件质心的坐标系简化，可以得到机构的平衡方程表达式为：和　分别为构件i质心处受水平和竖直方向的加速度；Ji和　分别表

式中，Fdi和Mdi表示构件i的驱动力和驱动力矩；mi为构件i的质量；示构件i质心处的转动惯量和角加速度；Fji为构件i在转动副处所受到的来自相连构件的约束反力。

本节建立的动态静力学问题是已知机构运动状态和外力情况，求解原动构件上的平衡力或平衡力矩（驱动力或驱动力矩），以及各转动副中的约束反力，即已知运动求力。因此，根据式（2.3.1）建立n个运动构件的3n个平衡方程，可以得到该机械系统的力平衡矩阵：

式中，K为未知变量的系数矩阵，为已知矩阵，其值取决于机构的运动学参数；N为未知变量向量；B为已知变量向量，主要为惯性参数。当未知变量个数为3n时，机构为静定机构，方程可以求解。若未知变量的个数大于3n时，机构为超静定机构，机构中存在过约束，需要给出与静不定次数相等数量的变形协调方程作为补充方程进行求解。

达朗贝尔原理对平面机构动力学建模的过程简明易懂，不易出错，且可以求解全部转动副反力及驱动力/力矩。因此本章将在对高速重载机械压力机传动机构运动学分析的基础上，利用达朗贝尔原理建立构件的力/力矩平衡方程，并对机构进行动力学性能计算与分析。

当高速重载机械压力机高速运行时，在转动副间隙和冲击载荷作用下传动机构以及机身不可避免地会发生振动与变形，且各振动与变形因素之间存在一定的耦合现象，本章只考虑主要因素，忽略相对次要因素开展高速重载机械压力机传动机构动力学分析，为此做如下假设条件：

（1）忽略传动机构中各构件前后方向振动与变形对动力学模型的影响；

（2）传动机构的内力除与载荷有关外，还与各构件的相对刚度有关，相对刚度越大的构件，其变形越小。由于各构件的刚度较机身、滑块和导轨而言要低得多，其在冲击载荷作用下只会产生位移和转角，忽略自身变形，因此假设传动机构中构件为刚体；

（3）假设传动机构中各运动构件的材料具有连续性、均匀性及各向同性；

（4）不考虑各转动副和移动副处的变形和间隙；

（5）忽略由装配误差和温度变化而产生的装配应力与温度应力引起的变形；(www.daowen.com)

（6）由于转动副润滑充分，摩擦阻力相对主动力和惯性力小得多，且变化规律很难精确掌握，因此在本章计算过程中忽略摩擦阻力对传动机构动力学特性的影响；

（7）忽略加工误差导致的构件尺度变化。

图2.3.2　传动机构受力分析图

在对高速重载机械压力机传动机构动力学分析的基础上，根据上述基于达朗贝尔原理的动力学建模理论，对如图2.3.2所示的高速重载机械压力机传动机构进行构件拆分，分别给出各构件的受力分析简图，进而可以得到在工作状态下高速重载机械压力机传动机构各运动构件的平衡方程：

根据上述建立的传动机构动态静力学模型，从传动机构力学方面入手，完成其关键构件的动态静力学分析，仿真计算参数如表2.3.1所示。

表2.3.1　动态静力学仿真计算参数

不同工况下传动机构各构件受力计算结果如图2.3.3和图2.3.4所示。由计算结果可以看出，空载状态下传动机构构件主要受重力和惯性力影响，构件所受载荷较小，曲柄载荷最大值为307.4 kN，平衡曲柄载荷最大值为317.9 kN。在冲压过程中，大部分工作载荷由连杆传递到曲轴上，对平衡机构几乎没有影响。其中，在最大工作载荷（7 500 kN）工况下，传递到曲轴上的最大载荷为3 748.5 kN，约为空载状态下载荷的12倍。由此可见，工作载荷对传动机构动态静力学特性的影响不容忽视。

图2.3.3　空载状态下各构件受力情况

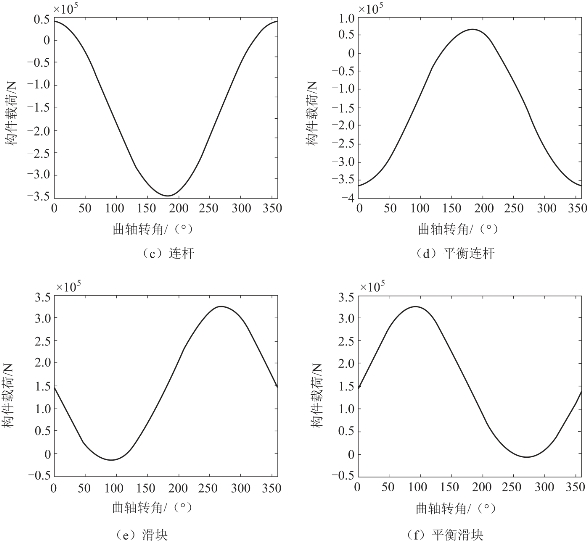
图2.3.3　空载状态下各构件受力情况（续）

图2.3.4　最大工作载荷状态下各构件受力情况

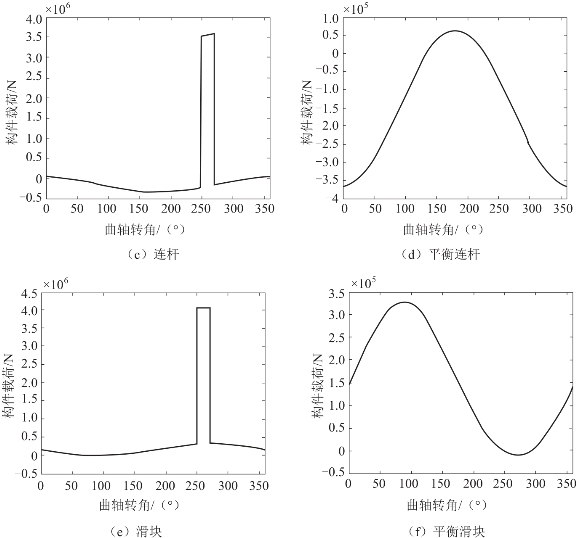
图2.3.4　最大工作载荷状态下各构件受力情况（续）