传动机构的运动学分析是建立在原动机构运动规律已知条件下，分析机构运行过程中各构件的运动学特性。通过传动机构运动学分析，可以得到该机构的运动轨迹，并为传动机构动力学分析奠定基础。

刚体是由无数点所组成，在点的运动学基础上可研究刚体整体的运动及其与刚体上各点运动之间的关系。刚体的平行移动和定轴转动是工程中最常见的运动，也是研究复杂运动的基础。

（1）刚体的平行移动。

工程中某些物体的运动，如气缸内活塞的运动、车床上刀架的运动等，它们有一个共同的特点，即如果载体内任取一直线段，在运动过程中这条直线段始终与它的最初位置平行，这种运动称为平行移动。

如图2.2.1所示，刚体内任意选两点A和B，令点A的矢径为rA，点B的矢径为rB，则两条矢端曲线就是两点的轨迹。当刚体平行移动时，线段AB的长度和方向都不改变，即恒矢量，此刚体上各点的轨迹形状相同，在每一瞬时状态下各点的速度和加速度也相同。因此，研究刚体的平移过程可以归纳为研究刚体内任一点（如质心）的运动，也可以将其看作点的运动学问题。

（2）刚体的定轴转动。

工程中最常见的齿轮、机床的主轴、电机的转子等，它们都有一条固定的轴线，物体绕此固定轴转动。显然，只要轴线上有两点是不动的，这条轴线就是固定的。刚体在运动时，其上或其扩展部分有两点保持不动，则这种运动称为刚体绕定轴的转动，简称刚体的转动。通过这两个固定点的一条不动的直线，称为刚体的转轴或轴线，简称轴。

如图2.2.2所示，为确定转动刚体的位置，取z轴为转轴，通过轴线作一固定平面A，同时通过轴线再作一动平面B，这个平面与刚体固结，一起转动。两个平面间的夹角（转角）用φ表示，转角φ对时间的一阶导数被称为刚体的瞬时角速度，而角速度对时间的一阶导数被称为瞬时角加速度。

图2.2.1　刚体平行移动示意图

图2.2.2　刚体绕定轴转动示意图

基于刚体位移原理[133-134]，将图2.2.3中所示的高速重载机械压力机传动机构部分简化为传动机构运动简图（图2.2.3）。取O点为坐标系原点，定义水平向右为x轴正方向，竖直向上为y轴正方向，建立高速重载机械压力机传动机构的位移矢量方程为：

将矢量方程（2.2.1）改写成解析表达式为：

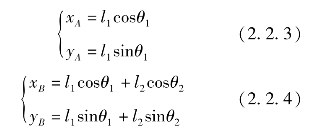
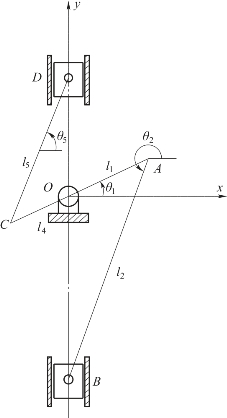
图2.2.3　传动机构简图

式中，l1为曲柄长度；θ1为曲柄与x轴正向夹角；l2为连杆长度；θ2为连杆与x轴正向夹角。

理想状态下，滑块水平位移为零，因此，连杆与x轴正向夹角表达式可以写成：同理可得，平衡机构解析表达式为：

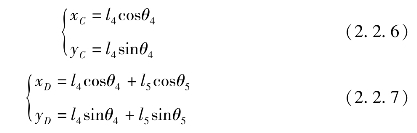
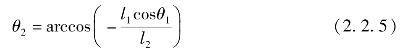
式中，l4为平衡曲柄长度；l5为平衡连杆长度；θ5为平衡连杆与x轴正向夹角；θ4=θ1＋π。

平衡连杆与x轴正向夹角的表达式为：

(www.daowen.com)

分别将式（2.2.3）和式（2.2.4）对时间求导可得构件速度运动方程为：

式中，ω1为曲柄角速度；ω2为连杆角速度。

进一步可以获得平衡机构速度运动轨迹表达式：

式中，ω5为平衡连杆角速度。

角速度表达式为：

将式（2.2.9）、式（2.2.10）对时间求导，分别得到构件加速度表达式为：

式中，α2为连杆角加速度。

同理可得，平衡机构加速度表达式为：

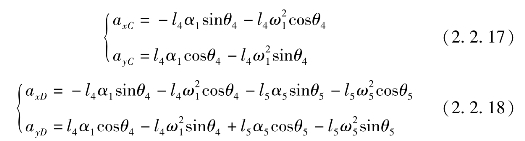
式中，α5为平衡连杆角加速度。

角加速度表达式为：

根据上述建立的理论计算模型，从传动机构运动学方面入手，完成其关键构件的运动学分析，仿真计算参数如表2.2.1所示。

表2.2.1　运动学仿真计算参数

不同转速下传动机构运动学仿真结果如图2.2.4所示。由计算结果可以看出，曲轴转速对滑块位移曲线没有影响，滑块位移曲线保持相同的运动轨迹，而曲轴转速对滑块的速度曲线和加速度曲线影响较大。随着曲轴转速的增加，滑块的速度和加速度明显增大。滑块速度的增加表明运行周期的加快，生产效率的提高，而滑块加速度的增大可能会引起惯性力的增加。由此可见，曲轴转速对传动机构运动特性的影响不容忽视。

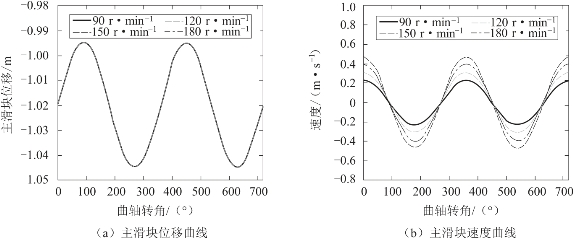
图2.2.4　传动机构运动学特性

图2.2.4　传动机构运动学特性（续）