高速重载机械压力机支承轴承动力学性能计算采用计算流体动力学法（CFD），而CFD计算分析过程基于有限体积法，本节对基于有限体积法的控制方程离散进行相关介绍[128-129]。

通常在对问题进行CFD计算前，首先要将计算区域离散化，即对空间上连续的计算区域进行划分，将其划分成多个子区域，并确定每个区域中的节点，从而生成网格。进一步，将控制方程在网格上离散，即将偏微分格式的控制方程转化为各个节点上的代数方程组。由于应变量在节点之间的分布假设及推导离散方程的方法不同，形成了不同的离散化方法：有限差分法、有限元法和有限体积法。

有限体积法（Finite Volume Method）基本思路是将计算区域划分为网格，并使每个网格点周围有一个互不重复的控制体积，将待解微分方程（控制方程）对每一个控制体积积分，从而得出一组离散方程，其中未知数是网格点上的因变量ϕ。为了求出控制体积的积分，必须假定ϕ值在网格点之间的变化规律。从积分区域的选取方法来看，有限体积法属于加权余量法中的子域法，从未知解的近似方法来看，有限体积法属于采用局部近似的离散方法。而离散方程的物理意义就是因变量ϕ在有限大小的控制体积中的守恒原理，如同微分方程表示因变量在无限小的控制体积中的守恒原理一样。有限体积法得出的离散方程，要求因变量的积分守恒对任意一组控制体积都得到满足，对整个计算区域也必须得到满足。就离散方法而言，有限体积法具有有限元法和有限差分法的特点。有限体积法只需求得ϕ的节点值，这与有限差分法相类似，但有限体积法在寻求控制体积积分时，必须假定ϕ值在网格点之间的分布，这与有限元法相类似。在有限体积法中，插值函数只用于计算控制体积的积分，得到离散方程后删除插值函数，在特定条件下，对微分方程中的不同项采取不同的插值函数。

与其他离散化方法类似，有限体积法的核心体现在区域离散方式上。区域离散化的实质是用有限个离散点来代替原来的连续空间。有限体积法的区域离散实施过程是将所计算的区域划分成多个互不重叠的子区域，即计算网格。再确定每个子区域中的节点位置及该节点所代表的控制体积，最后可以得到节点、控制体积、界面、网格线四种几何要素。在离散过程中，将一个控制体积上的物理量定义并存储在该节点处，如图1.4.2所示为一维及二维问题的有限体积法计算网格。(www.daowen.com)

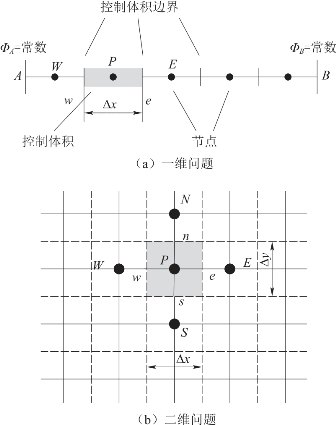
图1.4.2　有限体积法计算网格

为了便于后续分析，通过一套标记系统对网格几何要素进行标记。以二维问题为例，有限体积法所使用的网格单元（cell）主要有四边形和三角形两种，分别被称为结构网格与非结构网格。在结构网格中，与控制体积P相邻的四个控制体积及其节点分别用E、W、S、N表示，而控制体积P的四个界面分别用e、w、s、n表示，在两个方向上控制体积的宽度分别用Δx和Δy表示，如图1.4.2（b）所示。