物体受外部载荷作用所产生形状和大小的改变被称为变形,如果将引起变形的外部载荷移去后,物体能完全恢复到原来的形状和大小,这种变形称为弹性变形。当作用在物体上的外部载荷超过一定范围时,若再将外部载荷移去,物体不能完全恢复到原来的形状和大小,而是残留下来一部分永久的变形,这种变形被称为塑性变形。物体整个变形过程可以看成由两个不同的阶段组成,即弹性变形阶段和塑性变形阶段。将仅产生弹性变形的物体称为弹性体,弹性体内的应力与变形始终存在一一对应的单值关系,且许多情况下可以近似地按线性关系处理。
弹性体在载荷作用下,体内任意一点的应力状态可由6个应力分量σx,σy,σz,τxy,τyz,τzx来表示,其中σx,σy,σz为正应力,τxy,τyz,τzx为剪应力,应力分量及其正方向如图1.4.1所示。
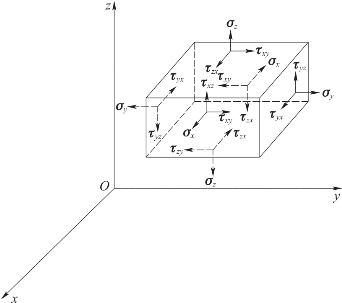
图1.4.1 应力分量及正方向
应力分量的矩阵表示形式为:
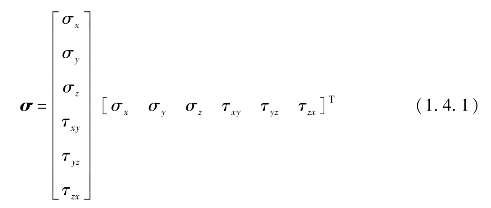
弹性体在载荷作用下,还将产生位移和变形,即弹性体位置的移动和形状的改变,弹性体内任意点的位移可由沿直角坐标轴的3个分量u,v,w来表示,其矩阵形式为:
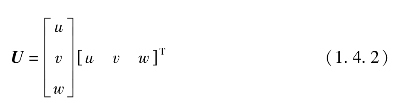
弹性体内任意一点的应变,可由6个应变分量εx,εy,εz,γxy,γyz,γzx来表示,其中εx,εy,εz为正应变,γxy,γyz,γzx为剪应变,而应变的矩阵形式为:
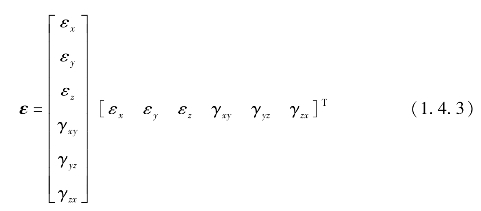
对于三维空间问题,弹性力学基本方程可改写成平衡方程的形式,弹性体V域内任一点坐标轴方向x,y,z的平衡方程为:
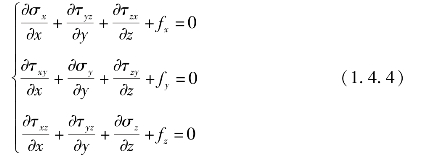
式中,fx,fy,fz为单元体积的体积力在相对方向上的分量。
平衡方程的矩阵形式为:
![]()
其中,A为微分算子:(https://www.daowen.com)
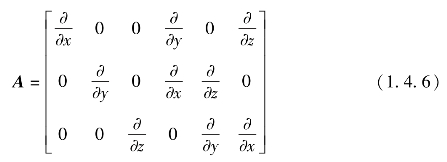
在微小位移和微小变形的情况下,略去位移导数的高次幂,则应变向量和位移向量间的几何关系:
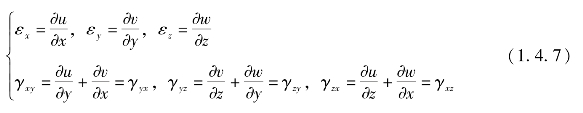
几何方程的矩阵形式:
![]()
其中,L为微分算子,其表达式:

弹性力学中应力-应变之间的转换关系也称弹性关系,对于各向同性的线弹性材料,应力通过应变的表达式可用矩阵形式表示:
![]()
其中,
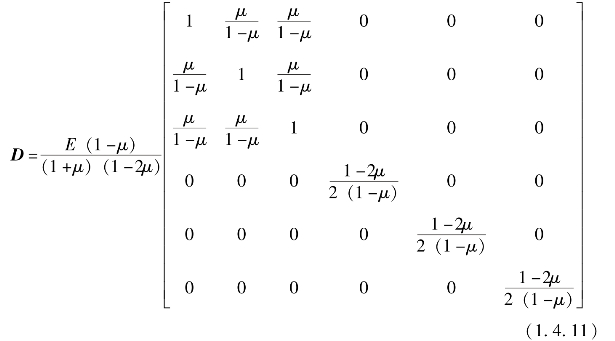
由式(1.4.11)可知,弹性矩阵取决于弹性体材料的弹性模量E和泊松比,而表征弹性体的弹性可用拉梅常数G和λ,其表达式为:
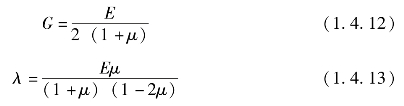
G和λ之间关系式为:
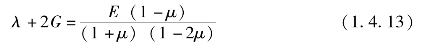
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







