一个电源可用电压源和电流源两种电路模型来表示,且电压源与电流源的外部特性相同,如图2-50所示。
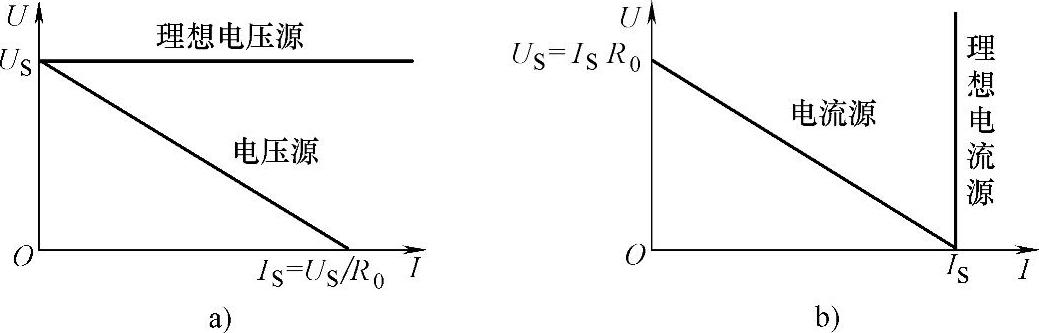
图2-50 电源的外特性
a)电压源的外特性 b)电流源的外特性
因此,电源的这两种电路模型之间是相互等效的,可以进行等效转换。两者之间进行等效变换的方法如图2-51所示。
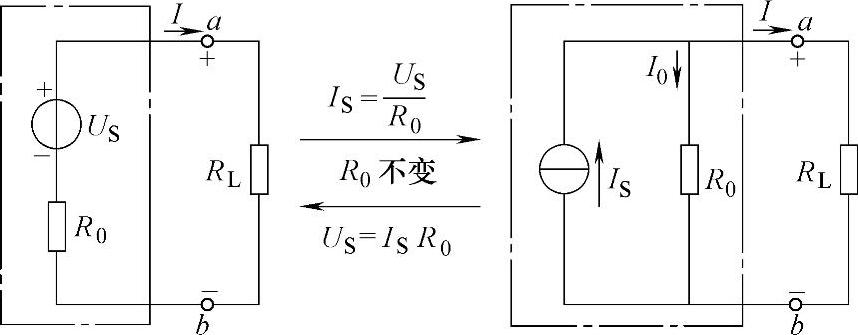
图2-51 电压源与电流源的等效变换
对于电压源与电流源的等效变换,特别需要注意的事项如下:
1)电压源和电流源的等效关系只是对外电路而言的,对电源内部是不等效的。
例如,在图2-51所示的电路中,当RL=∞时,电压源的内阻R0中不消耗功率,而电流源的内阻R0中则消耗功率。
2)电压源和电流源等效变换时,两电源的极性要一一对应,即电压源的正极与电流源输出电流的一端相对应。
3)理想电压源与理想电流源之间没有等效的关系。
因为对理想电压源(R=0)来讲,其短路电流IS为无穷大;对理想电流源(R=∞)来讲,其开路电压U0为无穷大。它们都不能得到有限的数值,故这两者之间不存在等效变换的条件。
4)任何一个电动势US(或E)和某个电阻R串联的电路,都可化为一个电流为IS的电流源和这个电阻R并联的电路。
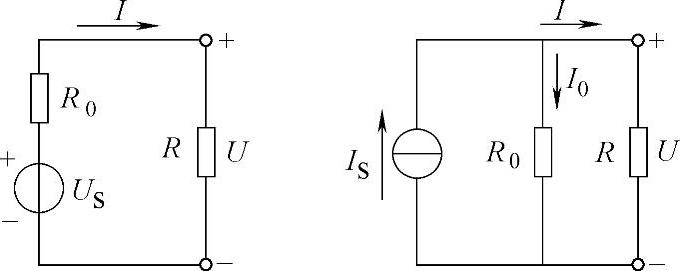
图2-52 例2-17图
【例2-17】在如图2-52所示的电路中,已知电源电动势US=6V,内阻R0=0.2Ω,当接上R=5.8Ω的负载时,分别用电压源模型和电流源模型计算负载消耗的功率和内阻消耗的功率。
解:1)用电压源模型计算:
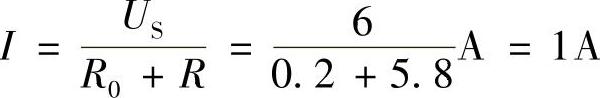
负载和内阻上消耗的功率分别为(www.daowen.com)
PL=I2R=12×5.8W=5.8W
PR0=I2R0=12×0.2W=0.2W
2)用电流源模型计算:
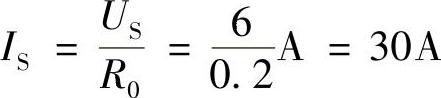
负载中的电流和负载消耗的功率分别为
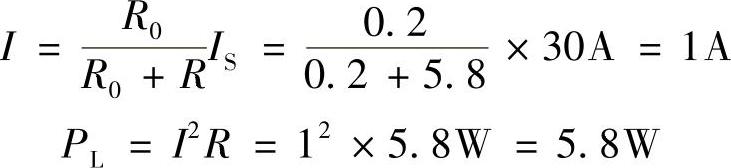
内阻中的电流和负载消耗的功率分别为
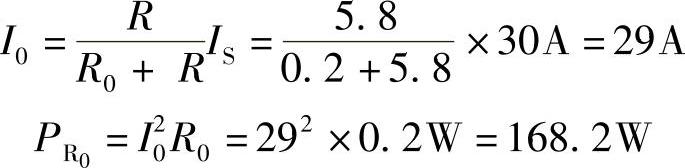
由此可见,两种计算方法对负载来说是等效的,对电源内部来说是不等效的。
【例2-18】如图2-53a所示的电路中,已知E1=12V,E2=6V,R1=3Ω,R2=6Ω,R3=10Ω,试应用电源等效变换法求电阻R3中的电流。

图2-53 例2-18图
解:1)先将两个电压源等效变换成两个电流源,如图2-53b所示。两个电流源的电流分别为
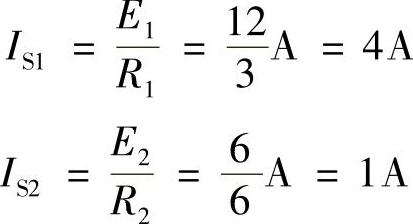
2)将两个电流源合并为一个电流源,得到最简等效电路,如图2-53c所示。等效电流源的电流及其等效内阻为
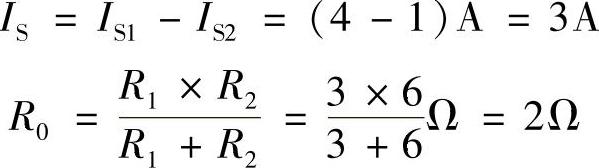
3)求得电阻R3中的电流为
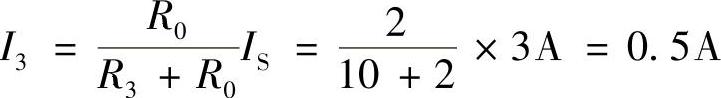
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






