【习题6.1】图6.4所示各梁，试画出梁挠曲线的大致形状。

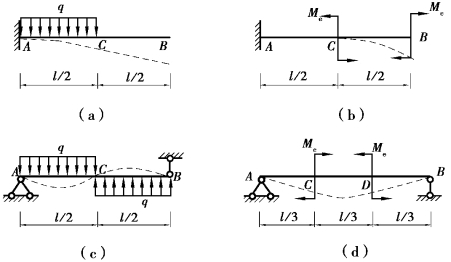
图6.4　习题6.1图

【解】绘制梁挠曲线大致形状的步骤为：

（1）作梁的弯矩图。

（2）由弯矩—曲率间的物理关系，确定挠曲线曲率的变化形状。

（3）根据梁的支座及构造情况，考虑变形协调条件，绘制挠曲线的大致形状。

各梁的弯矩图如图6.5所示，各梁挠曲线的大致形状如图6.4中虚线所示。

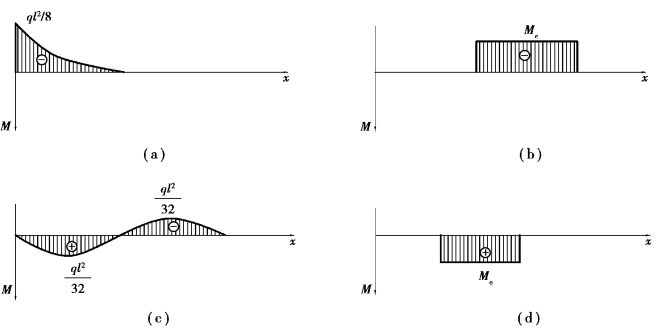
图6.5　各梁的弯矩图

【习题6.2】图6.6所示各梁，试画出梁挠曲线的大致形状。

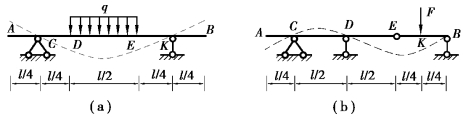
图6.6　习题6.2图

【解】绘制梁挠曲线大致形状的步骤为：

（1）作梁的弯矩图。

（2）由弯矩-曲率间的物理关系，确定挠曲线曲率的变化形状。

（3）根据梁的支座及构造情况，考虑变形协调条件，绘制挠曲线的大致形状。

各梁的弯矩图如图6.7所示，各梁挠曲线的大致形状如图6.6中虚线所示。

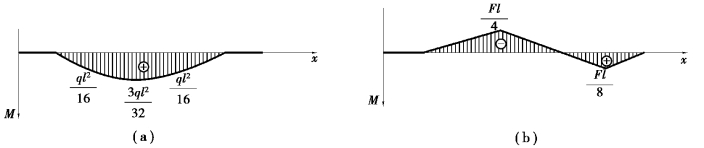
图6.7　各梁的弯矩图

【习题6.3】试写出图6.4所示各梁的边界条件和光滑连续条件。

【解】

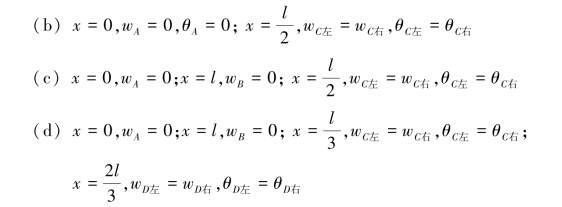
【习题6.4】试写出图6.6所示各梁E截面处的光滑连续条件。

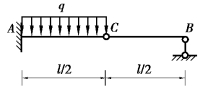
图6.8　习题6.5图

【解】

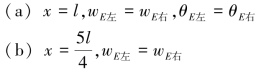
【习题6.5】试写出图6.8所示梁的边界条件和光滑连续条件。

【解】x=0，wA=0，θA=0；x=l，wB=0；x=，wC左=wC右

【习题6.6】试用积分法计算图6.9所示各梁的挠度方程、转角方程、最大挠度和最大转角。设梁的抗弯刚度EI为常数。

图6.9　习题6.6图

【解】（a）解：M（x）=-Me

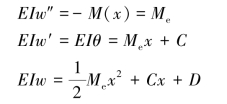
根据边界条件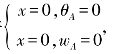　解得C=0，D=0

【习题6.7】试用积分法计算图6.10所示各梁的挠度方程、转角方程、C截面挠度wC和转角θC。设梁的抗弯刚度EI为常数。

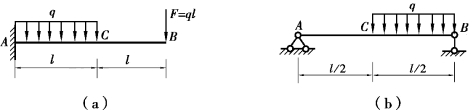
图6.10　习题6.7图

【解】（a）解：AC段：0≤x≤l

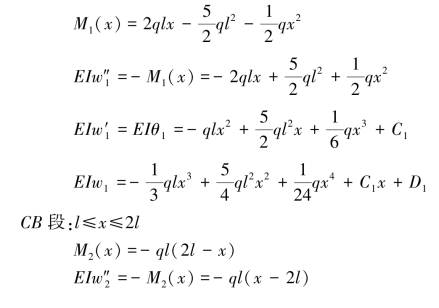
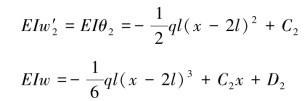
根据边界条件

【习题6.8】试用积分法计算图6.11所示各梁的挠度方程、转角方程、B截面挠度wB和转角θB。设梁的抗弯刚度EI为常数。

【解】（a）解：AC段：0≤x≤2l

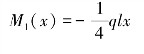
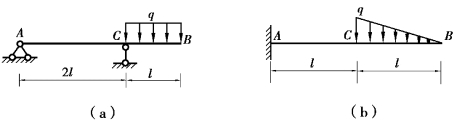
图6.11　习题6.8图

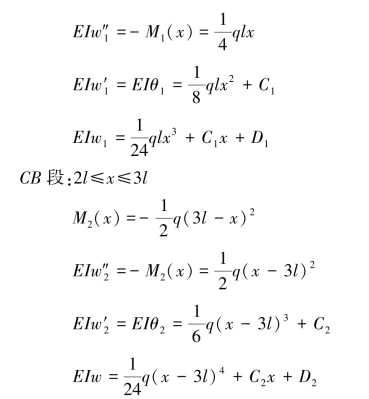
根据边界条件，

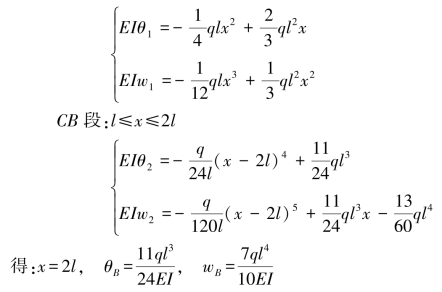
【习题6.9】试用积分法计算图6.12所示变截面梁的挠度方程、转角方程、C截面挠度wC和转角θC、B截面挠度wB和转角θB。设梁的抗弯刚度EI为常数。

【解】AC段：0≤x≤l

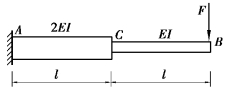
图6.12　习题6.9图

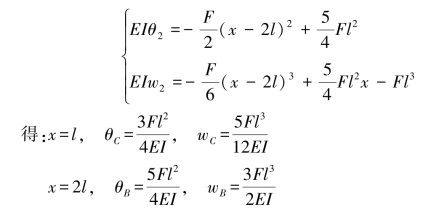
【习题6.10】试用积分法计算图6.13所示梁的挠度方程、转角方程、C截面挠度wC和B截面转角θB。设梁的抗弯刚度EI为常数。

【解】AC段：0≤x≤l

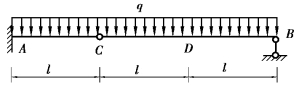
图6.13　习题6.10图

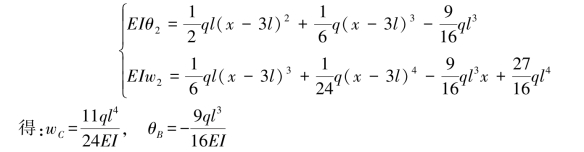
【习题6.11】试用叠加法计算图6.14所示各梁的C截面挠度wC和B截面转角θB。设梁的抗弯刚度EI为常数。

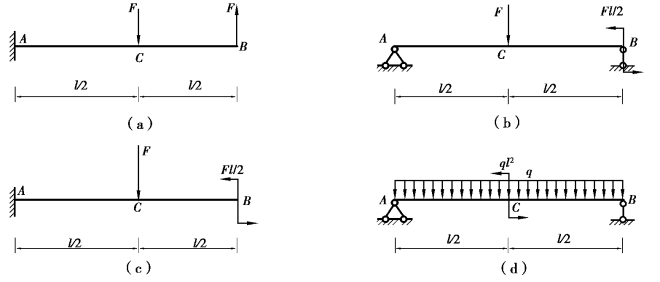
图6.14　习题6.11图

【解】（a）解：（1）分解荷载。将梁上荷载分解为集中力F单独作用的两种情况，如图6.15（a）和（b）所示。

图6.15　荷载分解图

根据叠加法可知，wC=wC1+wC2，θB=θB1+θB2

（2）查表求解。直接查表6.1可得

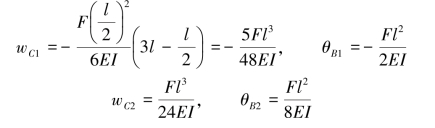
（3）叠加求和。

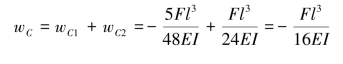
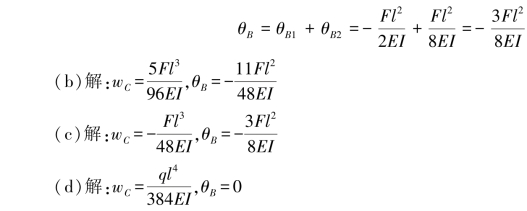
【习题6.12】试用叠加法计算图6.16所示各梁的C截面挠度wC和B截面转角θB。设梁的抗弯刚度EI为常数。

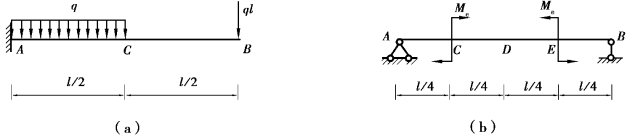
图6.16　习题6.12图

【解】（a）解：（1）分解荷载。将梁上荷载分解为均布荷载q和集中力ql单独作用的两种情况，如图6.17（a）和（b）所示。

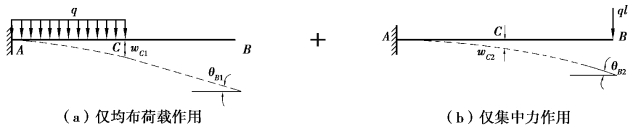
图6.17　荷载分解图

根据叠加法可知，wC=wC1+wC2，θB=θB1+θB2

（2）查表求解。直接查表6.1可得

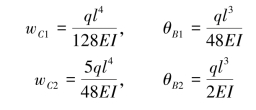
（3）叠加求和。(www.daowen.com)

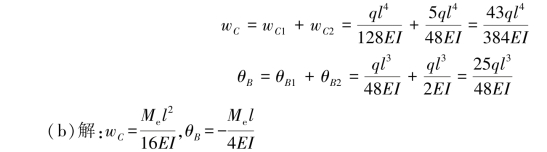
【习题6.13】试用叠加法计算图6.18所示简支梁的最大挠度wmax和最大转角θmax。设梁的抗弯刚度EI为常数。

【解】根据对称性，wmax在跨中D截面，θmax在铰支座A和B处，有θA=-θB。

（1）分解荷载。将梁上荷载分解为C截面、D截面和E截面单独作用集中力F的三种情况，如图6.19（a）、（b）和（c）所示。

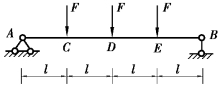
图6.18　习题6.13图

图6.19　荷载分解图

根据叠加法可知，wD=wD1+wD2+wD3，θA=θA1+θA2+θA3

（2）查表求解。直接查表6.1可得

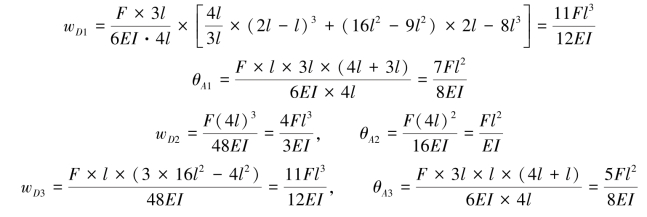
（3）叠加求和。

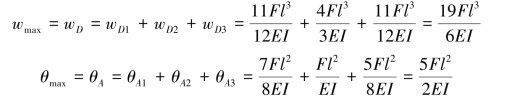
【习题6.14】试用叠加法计算图6.20所示各梁指定截面的挠度和转角。设梁的抗弯刚度EI为常数。

图6.20　习题6.14图

【解】（a）解：（1）分解荷载。将梁上荷载分解为集中力偶Fl和集中力F单独作用的两种情况，如图6.21（a）和（b）所示。

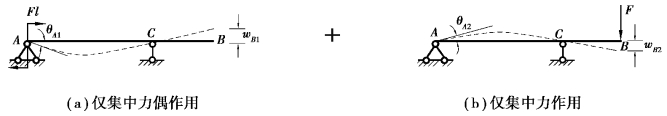
图6.21　荷载分解图

根据叠加法可知，wB=wB1+wB2，θA=θA1+θA2

（2）查表求解。直接查表6.1可得

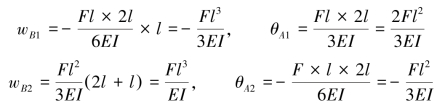
（3）叠加求和。

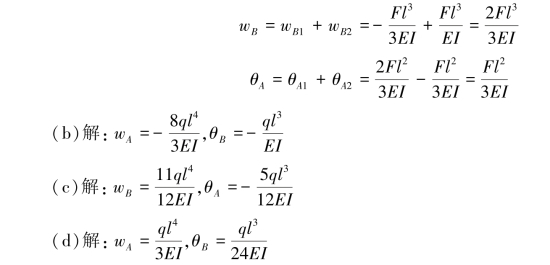
【习题6.15】试用叠加法计算图6.22所示简支梁的C截面挠度wC。设梁的抗弯刚度EI为常数。

【解】（1）分解荷载。将梁上分布荷载q进行分解，将其视为无穷个微小的集中力dF的组合，如图6.23所示。通过查表可以得到任一微小集中力dF单独作用时引起的变形，最后的叠加通过积分运算完成。

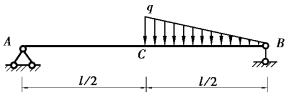
图6.22　习题6.15图

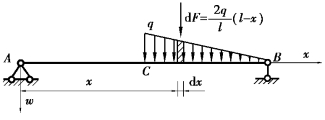
图6.23　荷载分解示意图

（2）查表求解。根据表6.1可知，距简支梁支座A距离x处的集中力单独作用时在跨中截面C处产生的挠度为

（3）叠加求和。

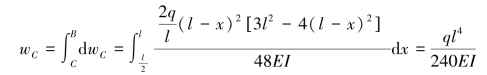
【习题6.16】试用叠加法计算图6.24所示变截面梁的C截面挠度wC和B截面转角θB。设梁的抗弯刚度EI为常数。

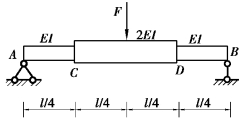
图6.24　习题6.16图

【解】由于对称性，原结构跨中的转角一定为零，且C截面的挠度与D截面挠度相等，即wC=wD。取其右边一半考虑，将梁跨中E截面设为固定端约束，右端铰支座用向上的作用力代替，如图6.25（a）所示，则图6.25（b）的悬臂梁与图6.25（a）的右半段梁的外荷载和内力完全相同，约束的几何效果相同，故原结构D截面的挠度与图6.25（b）中的悬臂梁自由端B截面相对于D截面的相对挠度数值相等，符号相反，即wD=-wBD。

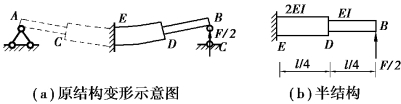
图6.25　荷载分解图

（1）分解荷载。将半结构受荷载作用发生弯曲变形，分解为仅ED段发生弯曲变形和DB段发生弯曲变形的两种情况，如图6.26（a）和（b）所示，有wBD1=wB1，wBD2=wB2。

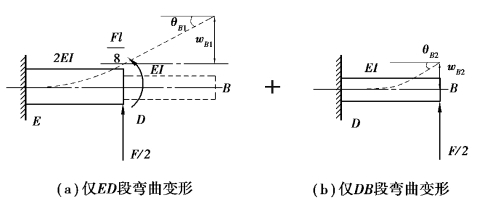
图6.26　荷载分解图

再根据叠加法可知，原结构D截面的挠度wD=-（wB1+wB2），θB=θB1+θB2。

（2）查表求解。直接查表6.1可得

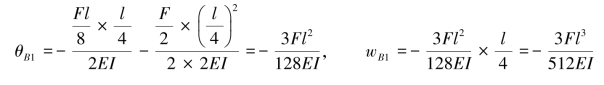
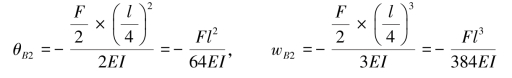
（3）叠加求和。

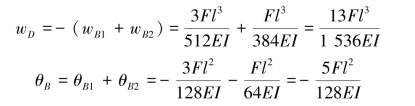
【习题6.17】试用叠加法计算图6.27所示各梁指定截面的挠度和转角。设梁的抗弯刚度EI为常数。

图6.27　习题6.17图

【解】（a）解：根据铰接梁的荷载和约束特点，梁上仅AC段发生弯曲变形，CD和DB段均不发生变形，仅有刚体位移发生，如图6.28所示。

查表6.1有

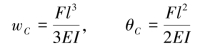
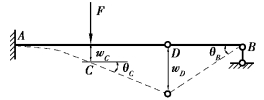
图6.28

故有

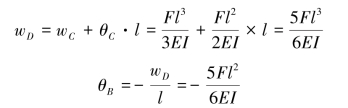
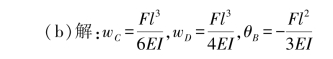
【习题6.18】如图6.29所示圆截面轴，两端用轴承支持，C截面处承受集中力F=1kN作用。若轴承处的许用转角[θ]=0.05rad，材料的弹性模量E=200GPa，试根据刚度条件确定轴径d。

【解】由题可知，当荷载F作用在C点时，轴承处B产生最大转角。查表6.1得

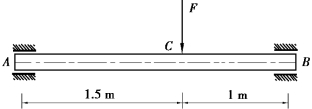
图6.29　习题6.18图

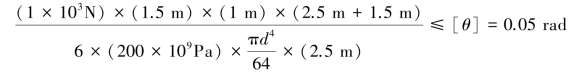
解得d≥30mm。

【习题6.19】如图6.30所示，一圆截面松木桁条受均布荷载q作用，已知木材直径d=200mm，许用应力[σ]=10MPa，E=10GPa，许用相对挠度为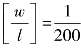，试计算均布荷载q的最大值。

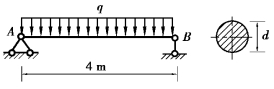
图6.30　习题6.19图

【解】（1）强度计算。最大弯矩为，则

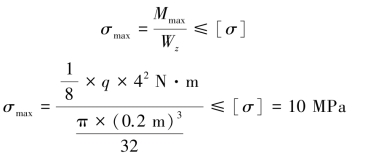
解得q≤3.93kN/m。

（2）刚度计算。查表6.1有

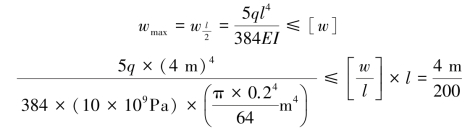
解得q≤4.71kN/m。

综上，均布荷载的最大值取3.93kN/m。

【习题6.20】图6.31所示悬臂梁，材料的许用应力[σ]=160MPa，E=200GPa。梁的许用相对挠度为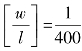，截面由两个槽钢组成，试选择槽钢的型号。

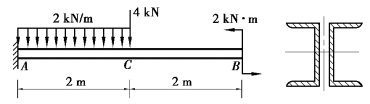
图6.31　习题6.20图

【解】（1）强度计算。最大弯矩为Mmax=10kN·m。设单个槽钢的抗弯截面系数为Wz，则

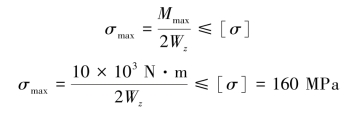
解得Wz≥31.3cm3。

按照强度条件，单个槽钢应选10号槽钢。

（2）刚度计算。根据叠加法，将悬臂梁所受荷载看成均布荷载2kN/m、集中荷载F=4kN及集中力偶M=2kN·m的叠加，如图6.32所示。设单个槽钢对中性轴z轴的惯性矩为I，查表6.1则有

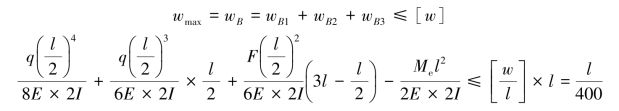
得I≥500cm4，则单个槽钢应选14a号槽钢。

综上，单个槽钢应选14a号槽钢。

图6.32　荷载分解图