【例题6.1】如图6.1所示，悬臂梁AB受集中力偶Me作用，试计算该梁的转角方程和挠度方程，以及该梁的最大挠度和最大转角。设抗弯刚度EI为常数。

图6.1　例题6.1图

【解】（1）建立弯矩方程。建立坐标系如图6.1所示，用截面法分段列出弯矩方程：

（2）建立挠曲线近似微分方程并积分。

（3）确定积分常数。

悬臂梁固定端处的挠度和转角均等于零，即

再考虑集中力偶Me作用位置C截面（荷载不连续处）的光滑连续条件，即

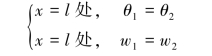
将边界条件和光滑连续条件分别代入式（a）、（b）、（c）和（d），可得

（4）建立转角方程和挠度方程。

将求得的积分常数值分别代入式（a）、（b）、（c）和（d），即可得转角方程和挠度方程，分别为

(www.daowen.com)

（5）计算最大挠度和最大转角。

梁上最大挠度和最大转角均出现在自由端A处，即x=0处，故将x=0代入式（e）中即可得。

本例题中，可先根据弯曲内力特点判断挠曲线的大致形状，由于CB段既无变形也无位移，则可利用积分法只考虑AC段从而简化计算。

【例题6.2】如图6.2所示，用叠加法计算外伸梁AC在均布荷载q作用下的θA、θB、θC、wC。设抗弯刚度EI为常数。

图6.2　例题6.2图

【解】（1）分解荷载。

将梁上荷载分解为图6.3（a）和（b）两种情况。

图6.3　荷载分解图

根据叠加法可知，θA=θA1+θA2，θB=θB1+θB2，θC=θC1+θC2，wC=wC1+wC2

（2）查表求解。查表6.1可得：

（3）叠加求和。