1）弯曲变形的概念

（1）挠曲线。平面弯曲时，梁的轴线弯成一条平面曲线，称为挠曲线或挠曲轴。

（2）平面弯曲时的变形。弯曲变形的程度可由挠曲线的曲率来度量。等直梁在纯弯曲下，挠曲线为圆弧线，其曲率为常量；在横力弯曲下，挠曲线曲率与该处的弯矩成正比。

（3）平面弯曲时的位移。

①挠度——横截面形心沿垂直于杆件轴线方向的线位移，用w表示，规定以向下为正，向上为负。

②转角——横截面绕其中性轴所转过的角位移，用θ表示，以横截面顺时针转动方向为正，逆时针转动方向为负。

2）梁的挠曲线近似微分方程

建立梁的挠曲线近似微分方程如式（6.1）所示，该方程仅适用于小挠度的计算。

3）积分法求梁的挠度和转角

对微分方程式（6.1）积分一次可得转角方程

再积分一次，可得挠度方程

当不连续时，则需要分段列出式（6.1）并进行积分。对于需要分n段的梁来说，在积分法的计算中，就会出现2n个积分常数。为了确定这些积分常数，就要充分利用梁的边界条件和光滑连续条件。(www.daowen.com)

边界条件：是指梁在其支座处的挠度或转角为已知的条件。

光滑连续条件：由于梁的挠曲线是一条光滑连续的曲线，故在同一截面上不可能有两个挠度值，在非中间铰处也不可能有两个转角值。

4）叠加法求梁的挠度和转角

（1）叠加原理。在小变形和材料线弹性的假定下，梁在多个荷载共同作用下所产生的挠度和转角等于各个荷载单独作用时挠度和转角的代数和。

（2）叠加法的使用。梁在简单荷载作用下的挠度、转角均已知，或由变形表（表6.1）可查。工程实际中，叠加法更适用于计算梁的最大挠度及最大转角。

表6.1　简单荷载作用下等截面直梁的挠度和转角

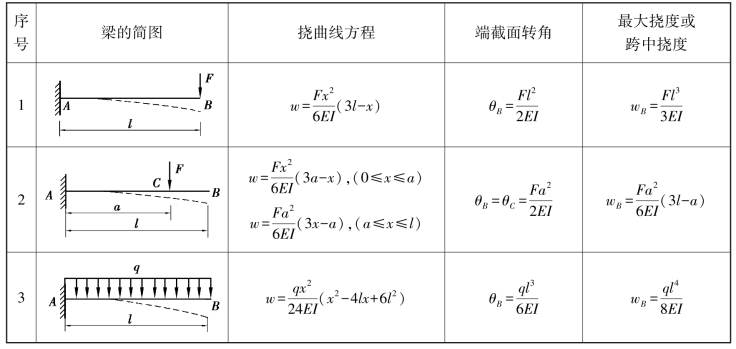
续表

续表

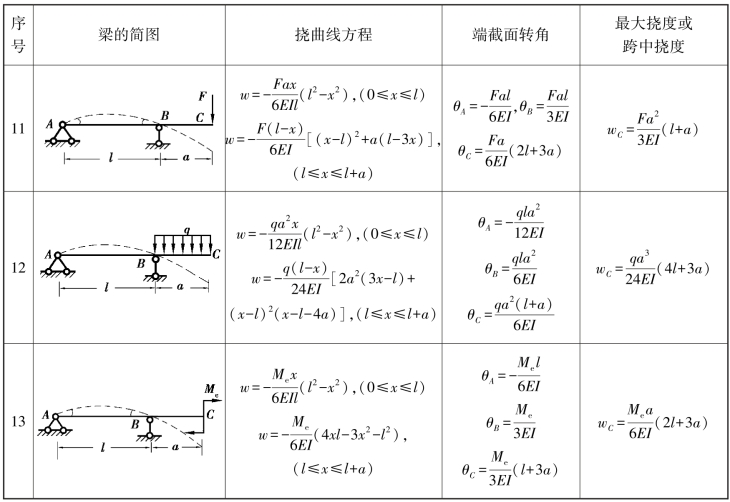
5）梁的刚度条件

（1）对于受弯杆件，除了强度条件，还必须满足刚度条件：

（2）提高梁弯曲刚度的措施包括：选用合理的截面形状，增大梁的抗弯刚度EI；改变加载方式，合理布置荷载位置；改善结构形式，合理布置支座位置；增加约束，采用超静定结构。