【例题4.1】试求如图4.1（a）所示外伸梁中C、D左邻和右邻截面上的剪力和弯矩。

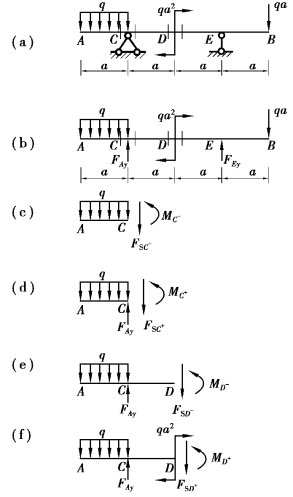
图4.1　例题4.1图

【分析】求解梁内力是正确绘制剪力和弯矩图的前提条件。通常求解梁横截面上的内力时，先要求支座反力。利用截面法求解梁内力时，通常假设所求内力的符号均为正的，这样求出来的结果符合内力正负规定，而无须说明，也可利用计算规律直接计算梁内力。

【解】（1）求支座反力。

首先，解除支座约束，代之以约束反力，作受力图，如图4.1（b）所示。设支座反力分别为FCy、FEy，根据静力学平衡条件求得：。

（2）求内力。

•方法一：利用截面法。

①欲求C左邻截面的内力，可沿C左邻截面将梁截开，取其左侧部分为研究对象，作受力图，如图4.1（c）所示。截面上的内力按剪力和弯矩的正负号规定，均画成正的。列出静力平衡方程：

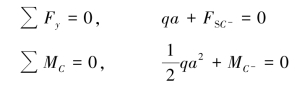
解得

②欲求C右邻截面的内力，同理，取其左侧部分为研究对象，作受力图，如图4.1（d）所示。列静力平衡方程：

解得

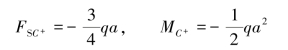
③欲求D左邻截面的内力，同理，取其左侧部分为研究对象，作受力图，如图4.1（e）所示。列静力平衡方程：

解得

④欲求D右邻截面的内力，同理，取其左侧部分为研究对象，作受力图，如图4.1（f）所示。列静力平衡方程：

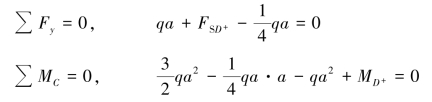
解得

•方法二：利用计算规律直接计算。

因为梁任一截面上的剪力和弯矩与该截面以左（或以右）梁上外力向该截面形心简化后的主矢和主矩大小相等，方向相反。所以梁内任一横截面上的剪力，在数值上等于该截面左侧（或右侧）梁上所有外力在垂直轴线方向上投影的代数和。梁内任一横截面上的弯矩，在数值上等于该截面左侧（或右侧）梁上所有外力（包括外力偶）对该截面形心的力矩的代数和。(www.daowen.com)

①C左邻截面的内力：

②C右邻截面的内力：

③D左邻截面的内力：

④D右邻截面的内力：

【例题4.2】利用q（x）、FS（x）、M（x）之间的微分关系绘制如图4.2（a）所示外伸梁的剪力图和弯矩图。

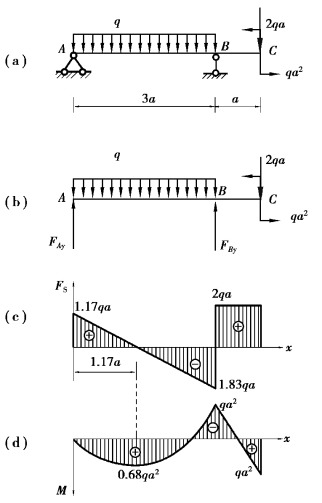
图4.2　例题4.2图

【解】（1）求支座反力。

首先，解除支座约束，代之以支座反力，作受力图，如图4.2（b）所示。根据静力学平衡条件求得：FAy=1.17qa（↑），FBy=3.83qa（↑）。

（2）剪力图绘制（至左向右）。

A截面上有向上的支座反力FAy=1.17qa，故A截面上的剪力向上突变，突变量为1.17qa，A处右邻截面的剪力为FSA+=1.17qa。

AB段梁上有向下的均布荷载q，剪力图为斜向下的直线，在B处左邻截面上的剪力为FSB-=1.17qa-3qa=-1.83qa。

B截面上有向上的支座反力FBy=3.83qa，故B截面上的剪力向上突变，突变量为FSB=3.83qa，B处右邻截面上的剪力为FSB+=-1.83qa+3.83qa=2qa。

BC段梁上无荷载作用，所以剪力为常量，均等于FSB+=2qa。

（3）弯矩图绘制。

AB段：梁上有向下的均布荷载q，所以弯矩图为向下凸的抛物线，且根据微分关系剪力FS=0处，即x=1.17a截面上，抛物线取得极大值Mmax=0.68qa2。

A截面无集中力偶作用，MA=0。

B处截面有支座反力，无集中力偶，故弯矩不发生突变。可计算得到MB=-qa2。

三点以一向下凸的平滑抛物线连接即为此分段弯矩图。

BC段：梁上无荷载作用，所以剪力为常量，故弯矩图为斜向下的直线。

C截面上作用有逆时针的集中力偶，在弯矩图上产生突变，突变量为qa2，在C处左邻截面上的弯矩为MC-=qa2。

以直线连接B、C两截面处的点，即为此分段弯矩图。