超声波声弹理论是目前用于测量应力的理论基础。声弹效应表明，在应力作用影响下，超声瑞利波在固体材料中的传播速度不同于未受应力作用的声波速度。由于激光熔覆层组织呈现明显的各向异性特征，材料的各向异性也会引起超声波传播速度的相对改变，因此需考虑组织效应及工作应力对于小振幅瑞利波传播的影响，推导激光熔覆层中的瑞利波声弹方程。

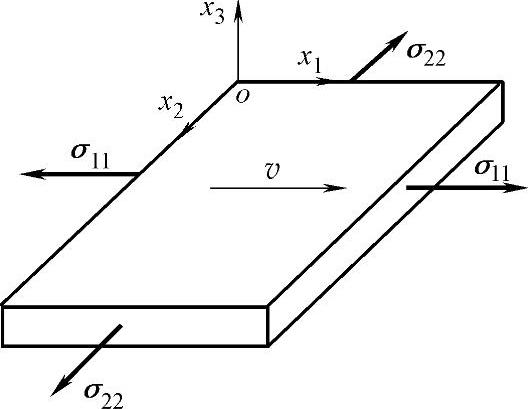
图6-1 激光熔覆层中的瑞利波波矢

取图6-1所示的坐标系，假设瑞利波在熔覆层表面以速度v沿着x₁方向传播，则瑞利波位移矢量所在的平面平行于x₁ox₃坐标平面，其中沿着x₃方向的传播深度为距离表面1～2个波长。通常情况下激光熔覆层厚度不大，并且沿厚度方向拘束度小，为自由表面，所以垂直于表面的正应力和平行于表面的切应力都等于0，因此熔覆层表层应力状态可简化为平面应力状态。根据材料力学理论，平面应力场上的应力可分解为多组不同取向的互相垂直的应力，假设被测微区内的应力状态如图6-1所示，x₁、x₂方向的应力σ₁₁、σ₂₂在被测微区内均匀分布，则依据有限变形理论，瑞利波波动方程可表示为

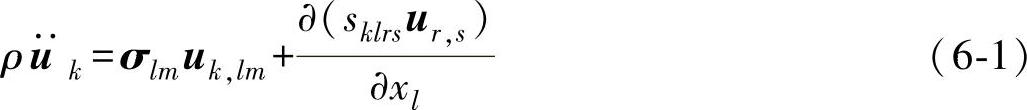
式中，k、l、m、r、s为张量下标；u_r，s=∂u_r/∂x_s；s_klrs=λδ_klδ_rs+μ（δ_ksδ_lr+δ_klδ_ls）+2λ（ε_klδ_rs+ε_kl）+[-λδ_klδ_rs-μδ_ksδ_lr+（λ-μ）δ_klδ_ls]ε_kk+2μ（ε_ksδ_lr+ε_lrδ_ks+ε_krδ_ls+ε_lsδ_kr）；ε为应变分量。

熔覆层表面为固体与空气的交界面，由于在空气中瑞利声波的传播极其微弱，所以边界条件可表示为

σ_3j=0（x₃=0，j=1，2，3） （6-2）

由波动方程和边界条件，可以得到熔覆层中质点位移沿三个坐标方向的分量

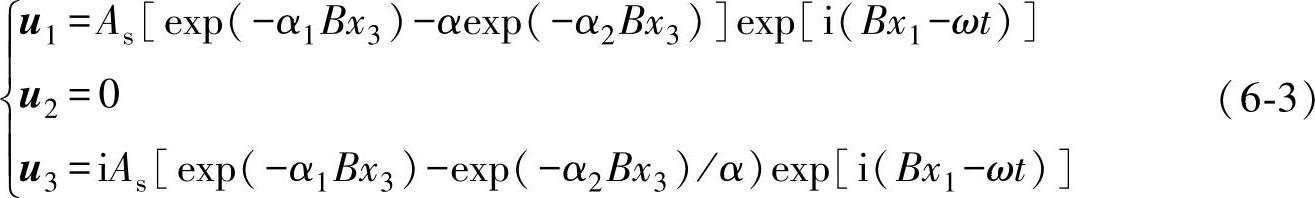
式中，A_s为材料特性有关的常数；ω为圆频率；B=ω/v；α₁=[1-（v/v_l）²]^1/2；α₂=[1-（v/v_t）²]^1/2；α=（α₁α₂）^1/2；v_l、v_t为无应力状态下熔覆层中纵波、横波的传播速度。

根据固体介质本构关系，边界条件又可表示为

σ_mju_3，m+s_3jrsu_r，s=0 （6-4）(www.daowen.com)

将式（6-1）和式（6-3）带入式（6-4），可得

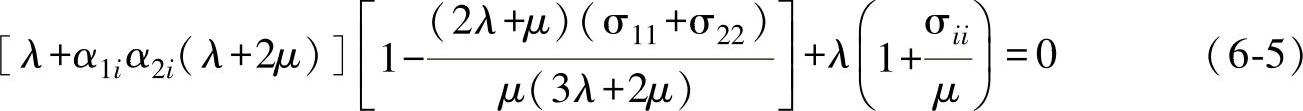
式中，σ_ii下标不做求和处理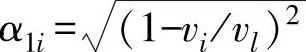；，i=1，2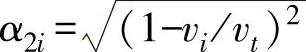；，i=1，2。

由式（6-5）可知，激光熔覆层中的表面应力与瑞利波传播速度之间存在着复杂的非线性关系，实际应用过程中，由应力引起的瑞利波速度变化量非常小，因此可用v₀处泰勒级数展开式对式（6-5）进行简化处理，忽略高次项，可得到瑞利波速度变化率与应力间的近似表达式为

Δv/v₀=（v_i-v₀）/v₀=σ₁₁k_i1+σ₂₂k_i2 （6-6）

式中，v₀为无应力状态下瑞利波的传播速度；

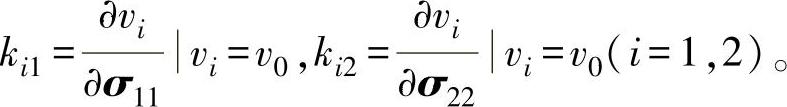
式（6-6）即为激光熔覆层中瑞利波的声弹方程，应力检测过程中，通过测试已知应力作用下材料中瑞利波声速的变化可以标定声弹系数k_i1、k_i2（i=1，2）。

由式（6-6）可知，k_i1、k_i2（i=1，2）为两互相垂直方向上介质的声弹系数。因此，采用表面超声波检测介质表层应力，首先需要对这两个系数进行标定。在万能试验机上对激光熔覆试样进行静载拉伸，载荷的加载方向与表面超声波的传播方向如图6-2所示。

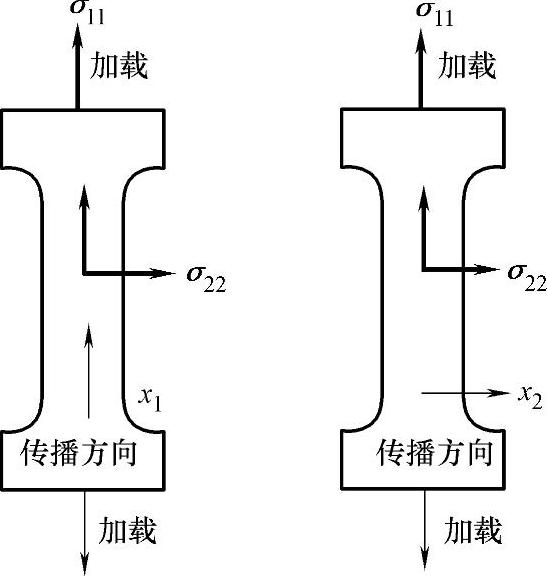
图6-2 加载方向与表面超声波传播方向示意图