1.检测方向对缺陷评价的影响

数值模拟结果表明，对于各向异性的激光熔覆组织，当检测方向与晶粒取向一致或垂直时，声束的偏转角度为零且辐射声场相对于入射轴线保持均匀的对称分布，声束的指向性最好。由3.1节Fe314熔覆层内部微观组织特征分析可知，其内部存在定向生长的柱状晶、树枝晶，并且组织中存在许多层与层之间的结合界面以及道与道之间的搭接界面，这些界面呈“直线”形或“圆弧”形。因此，超声纵波沿着不同方向传播时，遇到的组织、界面特征不同，声束的传播特性、能量衰减程度也不同，从而影响缺陷检测结果的可靠性。

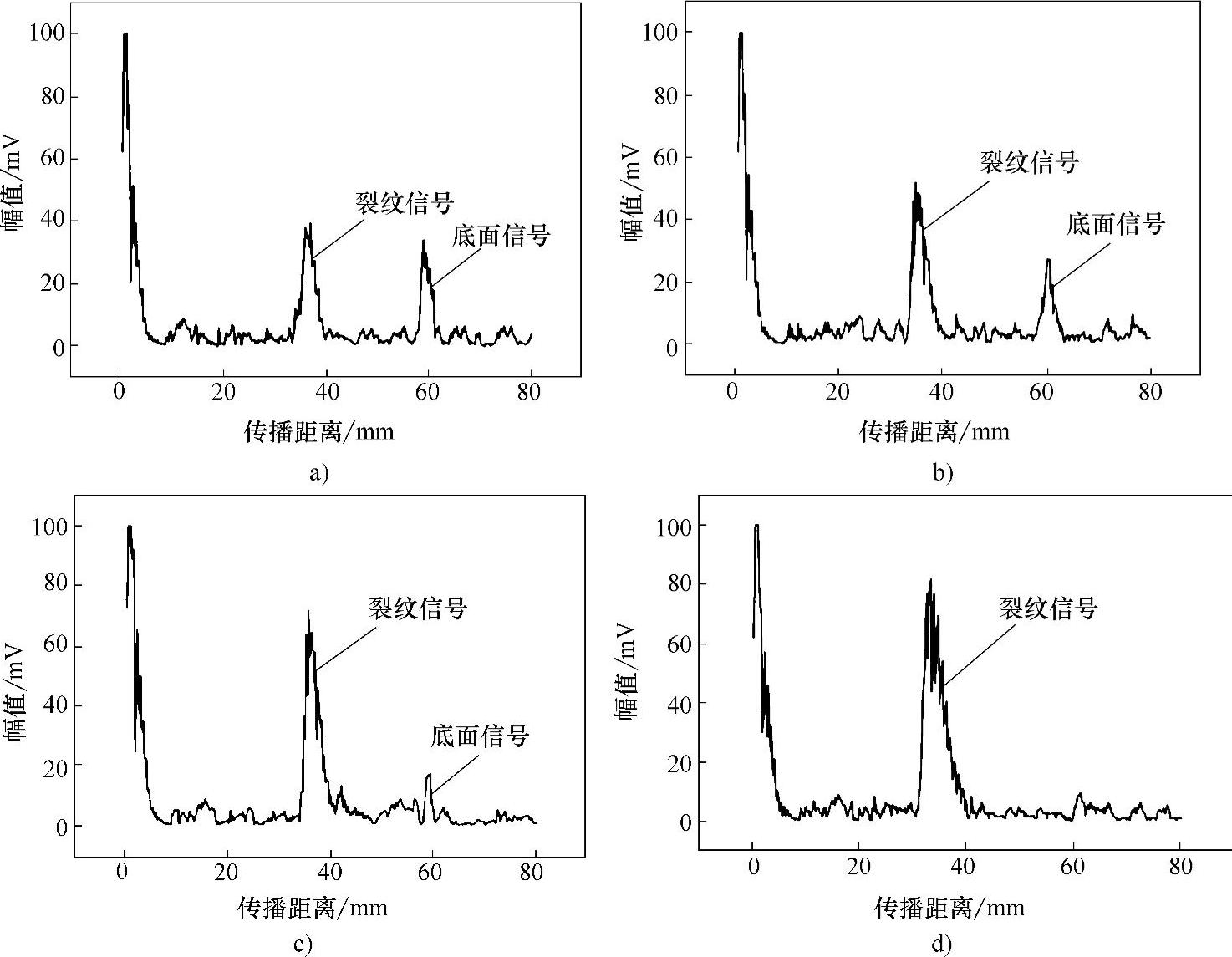
图5-5 不同长度裂纹超声纵波信号

a）3.0mm b）5.0mm c）7.0mm d）10.0mm

为了比较不同检测方向对超声纵波检测结果的影响程度，采用相同的检测参数，采集平行于基体结合面的超声波信号（见图5-7a所示平行于熔覆路径的方向1以及垂直于熔覆路径的方向2）、垂直于基体结合面的超声波信号（见图5-8所示方向3）。

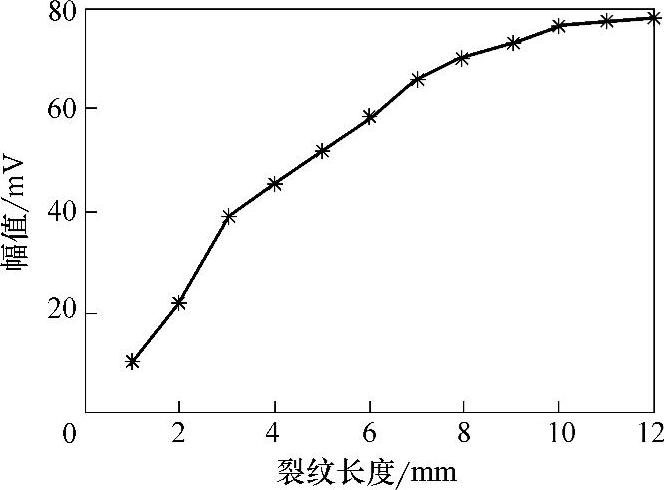
图5-6 裂纹缺陷信号幅值-裂纹长度关系曲线

由图5-7可知，平行于熔覆路径（方向1）的超声信号的信噪比明显高于另外两个方向超声信号的信噪比。原因在于三个不同方向上熔覆层内部微观组织对超声波的影响不同。从图5-8a可以看出，当超声纵波沿着方向1传播时，与超声纵波相互作用的界面主要是微观组织中柱状晶、树枝晶的界面，由于这些晶体比较细小，所以超声纵波与其作用产生的反射、散射能量损失比较小，探头接收到的信号中干扰信号少，信噪比较高；图5-8a中，当超声纵波沿着方向3传播时，与超声纵波相互作用的界面主要是熔覆层与熔覆层之间的结合界面，由于超声纵波的传播方向与这些界面垂直，所以在每一处界面都会产生较强的反射、散射、模式转换等行为，因此，这种情况下，超声纵波的能量损失比较严重，干扰信号也较多，所以探头接收到的信号信噪比低，甚至会产生波形畸变（见图5-5）；图5-8b中，当超声纵波沿着方向2传播时，与超声纵波相互作用的界面主要是熔覆道与熔覆道之间的搭接界面，超声纵波在每一处界面也会产生反射、散射、模式转换等行为，但由于这些搭接界面的面积总和小于超声纵波沿着方向3传播时与其相互作用的界面面积总和，所以超声纵波的能量损失较小，检测参数固定不变时，相比于探头在方向3接收到的回波信号，方向2接收到的回波信号具有更高的信噪比，波形畸变也比较小。

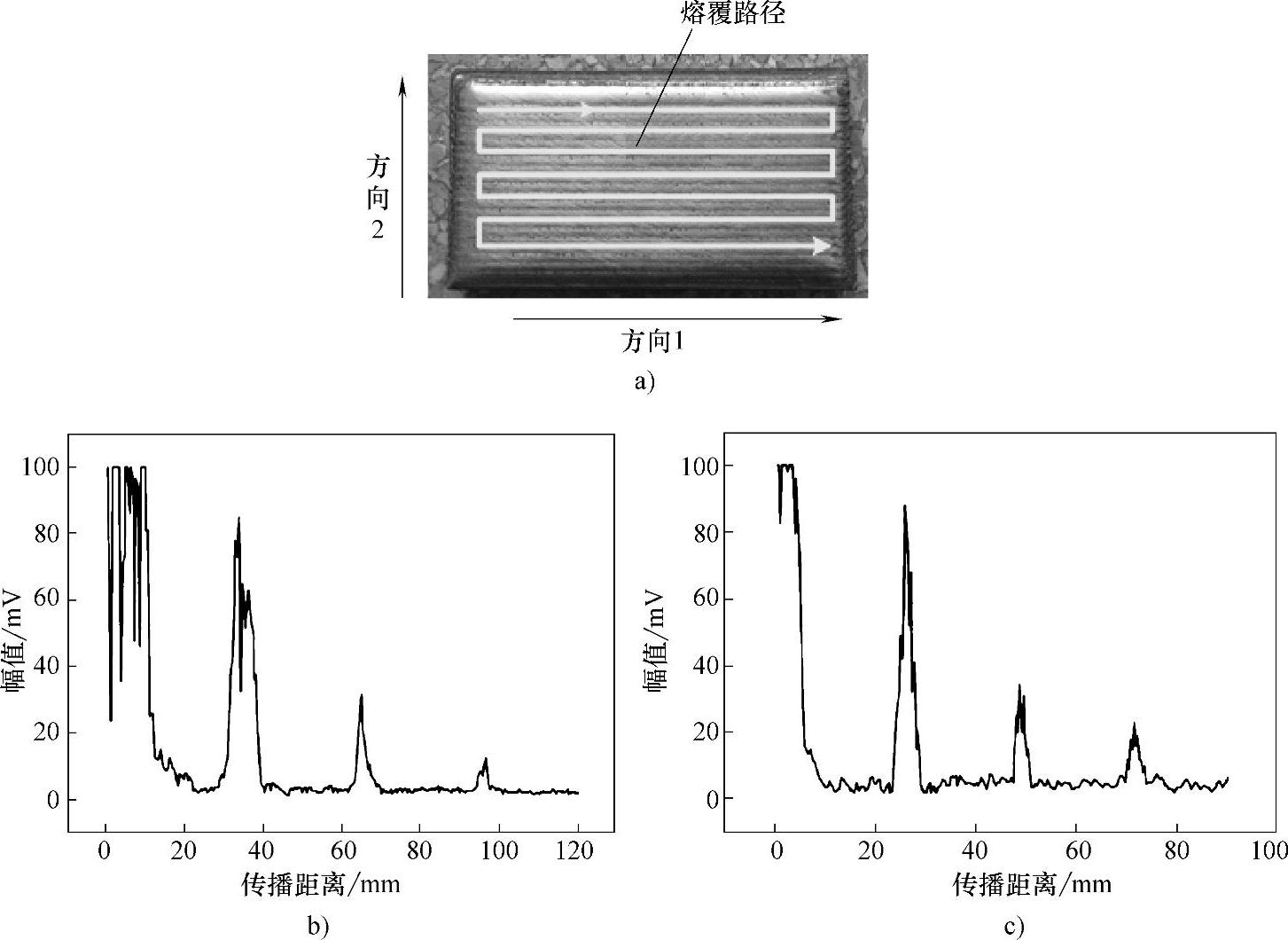
图5-7 不同检测方向的超声纵波信号

a）激光熔覆再制造试样及熔覆路径 b）平行于熔覆路径（方向1） c）垂直于熔覆路径（方向2）

总而言之，检测方向会直接影响各向异性Fe314激光熔覆层质量超声评价结果的直观性、可靠性，所以选择合适的检测方向非常重要。总结上述分析结果可知，检测Fe314激光熔覆再制造零件内部缺陷时，沿着平行于熔覆路径的方向1采集到的信号的信噪比最高，其次是垂直于熔覆路径的方向2、垂直于基体结合面的方向3，因此在条件具备的情况下（考虑缺陷延伸方向、埋藏深度对检测效果的影响）应尽可能沿着方向1进行缺陷扫查。

图5-8 方向1和方向2 Fe314激光熔覆层微观组织

a）方向1熔覆层组织 b）方向2熔覆层组织

2.检测距离对缺陷评价的影响(www.daowen.com)

通过上述分析可知，Fe314激光熔覆层的组织特征决定了超声波在传播过程中会产生非常明显的衰减，因此，采用当量法对熔覆层缺陷进行定量评价时，为了提高缺陷定量评价的可靠性应当考虑材料衰减的影响。本节研究检测距离对缺陷定量评价结果的影响及规律，探讨对其修正的方法。

以横通孔缺陷的定量评价为例，固定检测参数，改变Fe314激光熔覆层中横通孔缺陷距离表面的距离，采集一定检测距离下，不同直径横通孔缺陷的回波信号，建立横通孔缺陷的幅值—直径关系曲线。图5-9所示为不同检测距离下（15mm、25mm、35mm）横通孔缺陷的幅值—直径关系曲线。

由图5-9可知，不同检测距离下，横通孔缺陷信号的幅值—直径曲线变化趋势基本相同。但是随着检测距离的增大，相同直径圆孔缺陷的信号幅值逐渐减小，这说明超声纵波在Fe314激光熔覆层传播时，随着传播距离的增加，其能量的衰减是非常明显的。因此，为了提高熔覆层内部缺陷定量评价的可靠性，必须考虑传播距离引起的缺陷回波信号幅值的衰减量。

计算传播距离引起的信号幅值衰减量，首先要建立Fe314激光熔覆层试样中的超声纵波信号的幅值随传播距离变化的曲线。为此，采用双探头采集不同传播距离时的超声纵波信号，并对采集到的信号进行消噪处理，提取相应的接收信号幅值，建立图5-10所示的幅值—传播距离曲线。

建立了Fe314激光熔覆层试样中的超声纵波信号的幅值—传播距离曲线之后，需要采用合适的函数拟合该曲线。为此，需要掌握Fe314激光熔覆层试样中超声纵波的衰减规律，研究表明，引起超声波在介质中衰减的原因^[95]主要有三种：声束扩散、材料散射和吸收，Fe314激光熔覆层中主要考虑材料散射和吸收衰减，由于熔覆层晶粒直径远小于波长，因此其衰减规律可表示为

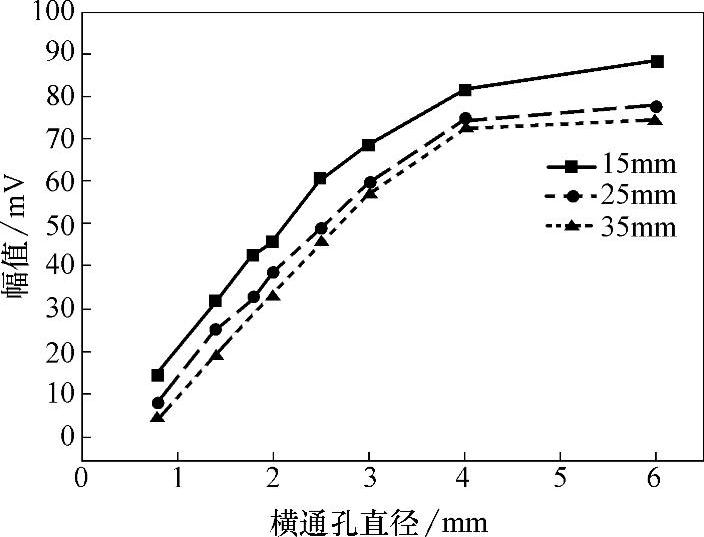
图5-9 不同检测距离下横通孔缺陷信号幅值—直径关系曲线

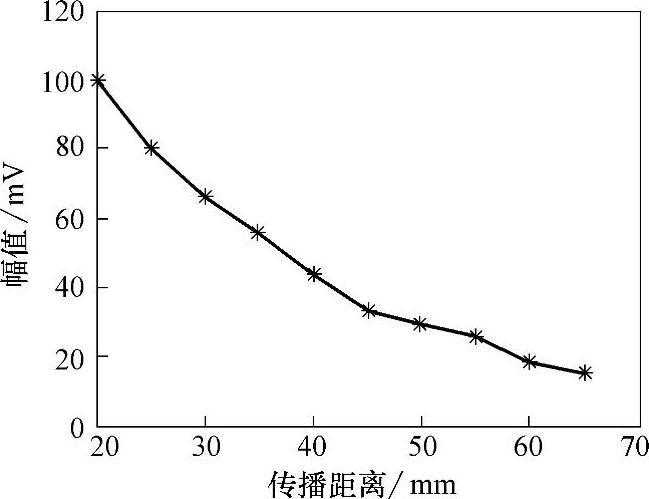
图5-10 Fe314激光熔覆层中超声纵波信号幅值—传播距离曲线

式中，A_x为传播距离为x处的振幅；A₀为探头处的振幅；x为超声纵波的熔覆层中的传播距离；C₁为介质弹性摩擦吸收系数；f为超声波频率；C₂为介质内散射体的瑞利散射吸收系数；d为晶粒尺寸。

由式（5-1）可知，超声波在Fe314激光熔覆层中的衰减规律符合指数函数变化，因此采用y=ae^bx对图5-10所示曲线进行拟合得：

A_x=229.8194e^-0.0414x （5-2）

由图5-9可知，当传播距离改变时，不同直径横通孔信号幅值的变化量基本相同，因此，采集一定检测距离下，不同直径横通孔缺陷的回波信号，建立横通孔缺陷的幅值—直径关系曲线，利用式（5-2）计算检测距离改变时缺陷信号的幅值改变量，就可以实现对激光熔覆层中不同检测距离处横通孔缺陷尺寸的当量评价。假定建立了传播距离为x₁的横通孔缺陷的幅值—直径关系曲线，采用与制作曲线相同的检测参数，检测到Fe314激光熔覆层中传播距离为x₂处有一圆孔缺陷，其信号幅值为A₂，为了对该缺陷进行定量评价，首先通过计算将其修正为x₁曲线上的点，即可求得缺陷的当量尺寸，则对应的x₁处的信号幅值为

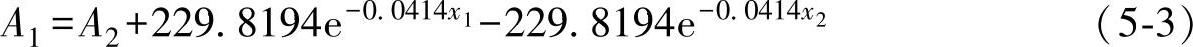
查找x₁曲线幅值为A₁的点对应的横坐标，即为Fe314激光熔覆层内部缺陷的当量尺寸。