1.小波母函数的选择

文献[152]指出，小波母函数的性质对小波包分析结果有着直接的影响，并且这种影响不容忽略。目前为止，应用小波包对超声波信号进行分析与处理的研究中，小波母函数的选择大多是根据前人总结的经验，并没有提出严格的理论依据。决定小波母函数性质的因素主要包括：支撑长度、对称性、消失矩阶数和正则性。对称性直接影响到信号的重构，如果小波母函数具有对称性，则重构信号就能很好地逼近原始信号，避免信号的失真；好的正则性对信号的重构能够获得好的平滑效果，非常有用；高阶消失矩有利于表现信号的高频部分，但不能获得紧支撑性，不利于时域的定位分析。结合超声波信号降噪目的，综合以上特性，选择具有紧支撑性、正交性以及近似对称性的symN小波族函数对超声波信号进行消噪处理。阶数N通过比较超声信号消噪前后的赋范均方误差来确定。

超声信号消噪前后的赋范均方误差为：

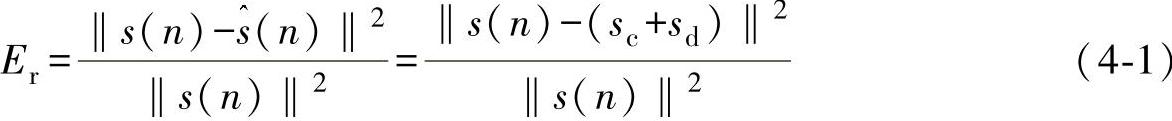
式中，s（n）为消噪前的信号；为消噪后的信号；n为采样点数；s_c、s_d分别为小波包分解的低频系数和高频系数之和。

用symN小波族函数对图4-1b所示的Fe314激光熔覆层试样表面超声波信号进行消噪处理，赋范均方误差如表4-1所示。

从表4-1可以看出，sym8小波的赋范均方误差明显小于其他小波函数的误差，综合考虑消失矩和支撑长度因素，选择sym8小波函数作为母小波对熔覆层超声信号进行消噪处理。sym8小波函数波形如图4-5。

表4-1 赋范均方误差统计结果

2.小波包分解层数的确定

实际应用中，通过实验发现，小波包分解的层数对超声波信号消噪效果有着重要影响，通常情况下，分解层数主要是根据实际经验预先设定好的。使用小波包分析可以将原始信号分解为近似分量（低频部分）和细节分量（高频部分），信号的噪声主要集中表现在信号的细节分量上。使用一定的阈值处理细节分量后，再经过小波包重构就可以达到消除噪声的目的。小波包分解时，随着分解层数的增加，噪声的能量会逐渐衰减，主要体现在噪声分解的小波包系数越来越小。因此不同信噪比的超声检测信号，理论上应当存在一个消噪效果相对比较好的分解层数。图4-6a、b分别为采用sym8最优小波包基对45钢及Fe314激光熔覆层中超声波信号进行6层分解得到的细节信号，从图中可以看出，d₁层～d₃层的超声波细节信号中存在明显的噪声，d₄层细节信号的噪声明显减少，d₅层、d₆层细节信号受噪声的影响已经非常小了，信号分布基本相同。因此，可以认为5层分解即可满足超声波信号消噪的要求。由4.1节的分析可知，噪声还会影响超声波信号频率的分布，为了清楚地分析45钢及Fe314激光熔覆层超声波细节信号频率的分布情况，对图4-6中各层细节信号做Hilbert包络及功率谱分析，结果如图4-7所示，对比两种材料细节信号功率谱可知，d₁层～d₄层细节信号的频率分布差别较大，d₅层和d₆层细节信号的频率分布基本相同。这与小波包分析的结果相同，即超声波信号的噪声主要分布在高频区，并且随着分解层数的增加，噪声会逐渐减小，但这并不意味着分解层数越多越好，当分解层数过多时，不仅会增加计算工作量，而且会造成信号中有用信息的丢失，从而使信噪比下降；分解层数过少，则不能有效消除噪声。因此选择合适的分解层数非常重要。

图4-5 sym8小波函数波形

分析实验结果可知，超声波细节信号中噪声分布与小波包分解层数是密切相关的，当分解层数达到一定数量j时，细节信号中噪声的含量与j-1层分解基本没有区别时，已经没有必要再分解下去，此时认为j-1层就是合理的分解层数。因此，确定分解层数的关键在于将超声波细节信号中不同分解层数噪声含量表达出来，并逐层进行比较。本书采用Shannon熵来表示信号中噪声含量的大小。

Shannon熵理论[153]指出，对于一个不确定系统，其状态特征可用有限个随机变量X表示，状态特征为X_j的概率为p_j=p{X=X_j，j=1，2，…，L}，则由状态特征X_j得到的信息可以用H_j=ln（1/p_j）表示，于是X的信息熵为

图4-6 不同材料超声波细节信号

a）45钢细节信号 b）Fe314激光熔覆层细节信号

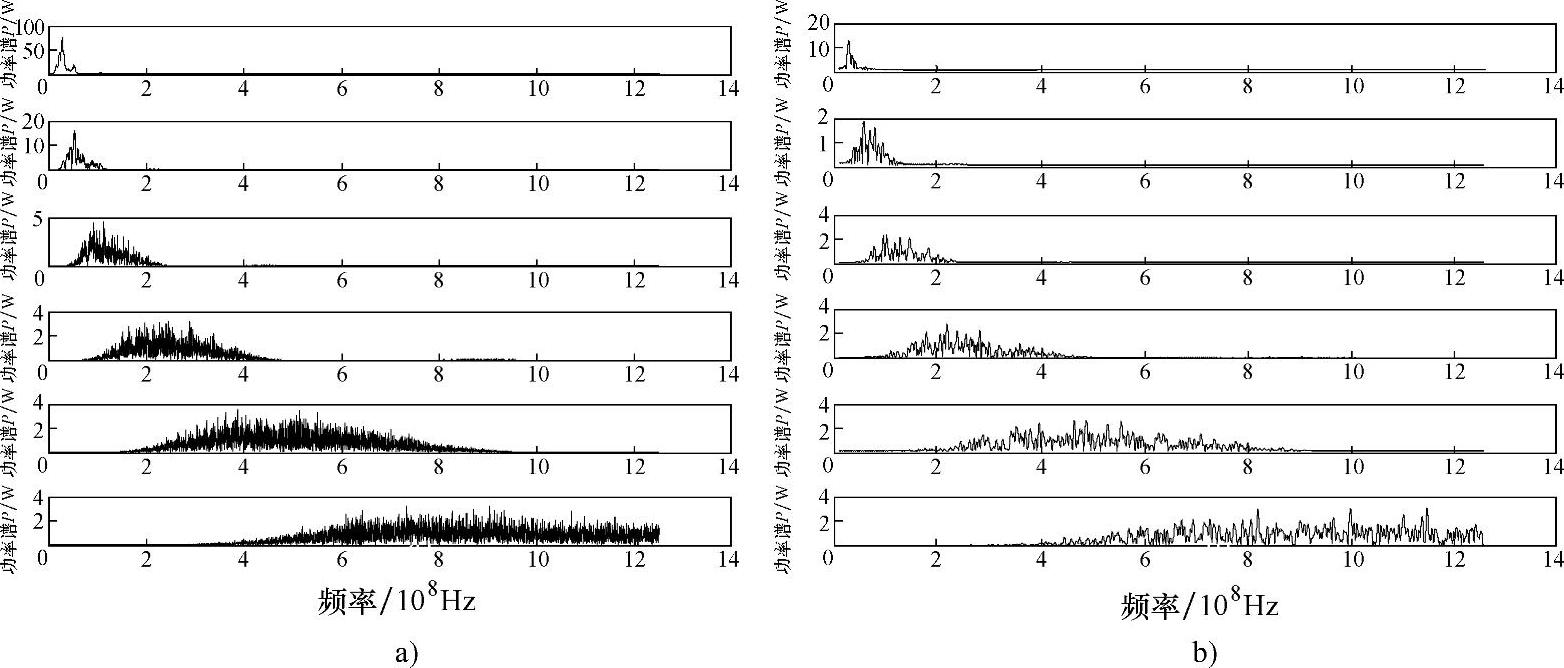
图4-7 不同材料超声波细节信号功率谱

a）45钢细节信号功率谱 b）Fe314激光熔覆层细节信号功率谱

当p_j=0时，p_jlnp_j=0。

若上述系统中，由于噪声干扰源的影响，随机变量X还可以取m个值，取值x_v的概率为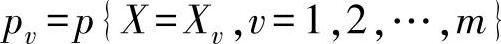，并且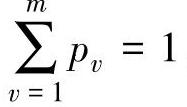，则含噪系统的熵

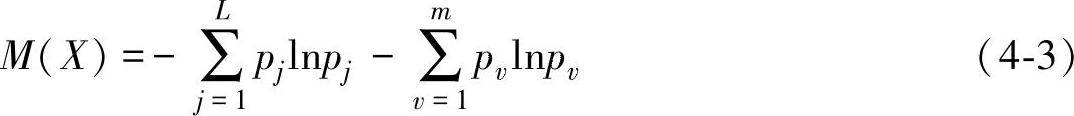
对比式（4-2）、式（4-3）可以发现，含噪系统出现了熵增，即系统的无序程度增加，因此可以用熵表征系统（如超声波检测信号）的含噪状态。超声波信号分解层数的确定方法如下（为了保证算法的收敛，设定最大分解层数j_max=8）：

1）设定小波包分解层数j=2。

2）采用sym8母小波对超声波信号进行j层分解。

3）计算第j层及j-1层细节信号的Shannon熵。

4）比较第j层及j-1层细节信号的Shannon熵值大小，如果|j_熵-（j-1）熵|≤1×10^-4，则分解层数为j-1，否则判断j≥j_max是否成立，若成立则分解层数为j，不成立则j=j+1，跳转到第2）步。

3.基于Shannon熵准则的最优小波包基分解原理

由小波变换的多分辨率分析[154]可知，给定正交尺度函数ϕ（t）和小波函数ψ（t），其二尺度关系为

式中，h_0k、h_1k为多分辨率分析中的滤波器系数；t∈R，k∈Z。为进一步推广二尺度方程，定义下列的递推关系

以上定义的函数集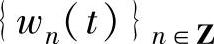为由w_o（t）=ϕ（t）所确定的小波包，小波包是包括尺度函数w_o（t）和小波母函数w₁（t）在内的一个具有一定联系的函数的集合。从小波包库中抽取的能组成L²（R）的一组正交基就称为L²（R）的一个小波包基。由图4-4可知，对一个信号的小波包分解可以用很多种小波包基来实现。因此，希望能找到一个最优的小波包基对信号进行分解[154]，不仅可以有效地表达出信号的特性，而且能够方便地对信号进行重构。

指导最优小波包基分解的特征函数主要是信息的熵（本书中采用Shannon熵）。熵是度量信息规律性的量，熵值越低，表明信息的规律性越强^[155]，在小包库的所有小包基中寻找使熵最小的基，该基就是信号分解的最优小波包基。从信息处理的观点来看，选择一个最优基进行分解，其实质是力图使分解有最强的规律性，把信号内在的规律都找出来。这样做的结果会使信号中隐含的能量集中反映在少数几个分解系数上，为信号处理中的数据压缩以及消噪处理提供一个较好的分解和重构途径。

选取最优基的算法采取自底向上的搜索方法。用U_j，n表示按二进制间隔划分的标准正交基，上层节点为父节点，下层节点为子节点。当分解层数为j时，共有2^j个节点。选取基F_j，n（0≤n≤2^j-1），F_j，n是U_j，n张成的空间。以最小Shannon熵为准则来选取j-1层的基F_j-1，n（0≤n≤2^j-1-1），令M_U=M（U_j-1，nX），M_F=M（F_j，2n+X）+M（F_j，2n+1X），分别表示X的以基U_j-1，n和（F_j，2n，F_j，2n+1）展开时的Shannon熵函数，递推搜索过程如下

可以证明，上述算法生成了信号X关于Shannon熵的最优基。搜索过程从最底层节点开始，逐层向上按二进制分支路径求出最小熵值。当两个子节点信息熵之和大于父节点信息熵时，保留父节点，去掉两个子节点，否则，保留两个子节点，并以子节点之和的信息熵代替父节点的信息熵，然后逐层向上进行比较，最终确定所采用的最优小波包基。

用sym8小波包对图4-1a、b的超声波信号进行三层分解，图4-8和图4-9分别是采用Shannon熵为代价函数搜索到的最优小波包基，图4-8所示45钢超声信号搜索到的最优小波包基节点为（3，0）、（3，1）、（3，2）、（3，3）、（3，4）、（3，5）、（2，3）。图4-9所示Fe314激光熔覆层超声信号搜索到的最优小波包基为节点（3，0）、（3，1）、（2，1）、（3，4）、（3，5）、（3，6）、（3，7）。由此可见，即使采用相同的小波包对不同的信号进行分解，得到的最优小波包基也不尽相同。(www.daowen.com)

图4-8 45钢超声信号最优小波包基图

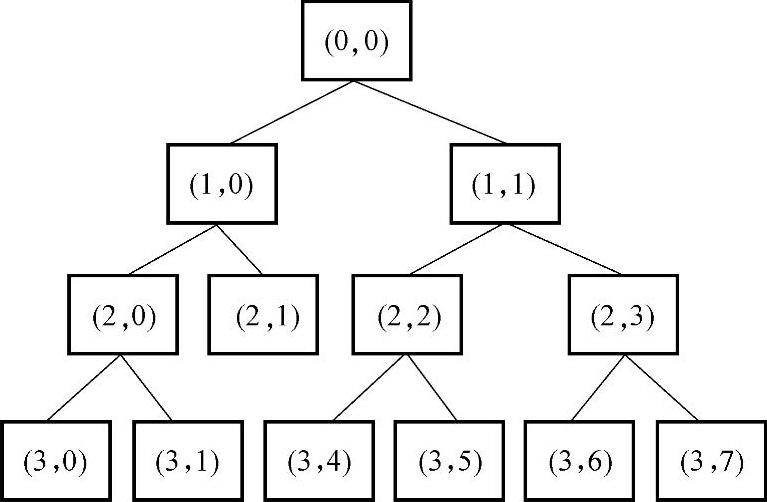
图4-9 Fe314激光熔覆层超声信号最优小波包基

4.最有小波包基消噪自适应阈值的确定方法

在小波包分解消噪过程中，要做到既去除大部分噪声，又不会引起重建信号的明显失真，除了分解层数要合适之外，阈值的选择与量化也非常关键。国内外很多学者提出了多种理论和经验阈值模型，例如Heursure阈值、Minmax阈值、Sqtwolog阈值等，采用这些阈值对高信噪比信号能够实现近似最优分离，但对信噪比较低或完全被噪声淹没的微弱信号，效果并不理想。针对各类经验阈值模型的不足，根据Shannon熵理论，本书提出根据小波能谱熵确定最优小波包基不同分解尺度的阈值，实现对低信噪比信号的有效去噪，提高材料内部缺陷诊断的准确度。

（1）超声信号模型及阈值选取 通常情况下，超声检测缺陷回波信号模型^[155]可表示为

f（t）=Aexp[-α（t-τ）²]cos[ω_c（t-τ）+ϕ] （4-7）

式中，A、α、ω_c、τ、ϕ分别为缺陷回波幅值、带宽因子、中心频率、缺陷回波返回时间和相位。

超声检测中的噪声主要有非声学噪声及声学噪声两类。一般认为非声学噪声（以e（t）表示）是白噪声，与缺陷回波信号不相关，在整个观测时域内服从正态分布。对超声波信号进行最优小波包基分解消噪时，由于非声学噪声在小波域对应的小波系数仍满足正态分布，这为利用信号的已知信息来寻求某种准则（如统计学分析）意义上的最佳阈值选取提供了可能，例如根据Donoho提出的软阈值^[156]方法，能够实现缺陷信号与非声学噪声的近似最优分离。Donoho软阈值为

式中，σ_q为分解尺度为q的小波包分解细节系数的噪声方差，d_q，l（l=1，2，3，…，N）为尺度为q的小波包分解细节系数，N为小波包分解系数的长度。

由式（4-8）可以看出，Donoho阈值不仅考虑了非声学噪声的统计学分布（正态分布）特征，也体现了噪声在不同分解尺度之间的差异，因而能够实现缺陷信号与非声学噪声的近似最优分离。

除了非声学噪声之外，激光熔覆层超声波信号中，还有声学噪声（也称材料散射噪声），声学噪声不同于非声学噪声，在扫描过程中，若换能器不动，不同次采样中的材料噪声近似相同。采用已有的各类经验阈值模型，对这类噪声的消噪效果不是很理想。要想通过小波包分析有效降低材料噪声对超声检测信号的影响，分析材料散射噪声小波包分解系数的统计分布特征，选取合适的阈值是解决问题的一条有效途径。

通常情况下，不考虑材料中各晶粒间的超声波多次散射，材料散射噪声的回波信号模型可表示为

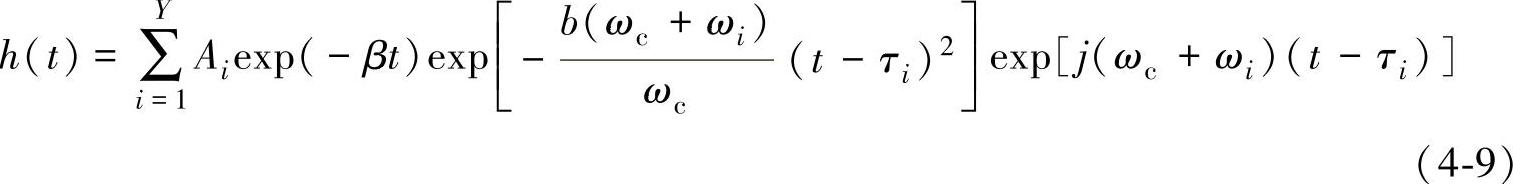
式中，Y为超声探测声束覆盖范围内的晶粒数；A_i为散射回波的幅值；β为衰减常数；b为大于零的常数，其值越大，散射回波在时间上持续越短；ω_c为中心频率；ω_i为材料散射噪声对入射超声信号频率的飘移；τ_i为材料噪声回波返回的时间；ω_i、τ_i为在整个观测时域内服从均匀分布的随机数。

考虑上述两类噪声的缺陷回波信号s（t）模型为

s（t）=f（t）+h（t）+e（t） （4-10）

由式（4-7）、式（4-10）可知，材料散射噪声对应的小波系数在部分时间-尺度区间上与缺陷回波信号是相关的，也就是说这类噪声在特定的时间-尺度区间上分布较为集中。分析超声波信号小波包分解系数在某一尺度不同时间段的分布特征，找出噪声分布最集中的区域，利用鲁棒估计法估计该区域内的小波包分解系数的噪声方差，然后按照（4-8）式计算阈值，就可以有效降低材料散射噪声，因此关键在于如何找出噪声分布最集中的区域。

（2）基于Shannon理论自适应阈值的确定 由前述分析可知，为了有效消除超声波信号中的噪声，应当根据噪声能量的变化选择阈值，噪声能量的大小可以用信息熵来表征，因此将小波包变化与信息熵结合，就可以得到小波包能谱熵计算方法。将信号s（t）进行最优小波包基分解，然后根据时间特性将尺度q的小波包节点细节系数等分成g段，然后计算每一时间段内的信号能量。定义尺度q小波包节点细节系数第r个分段信号能量为

式中，q为分解尺度，d_q，l表示第r个分段内第l个细节系数。由正交小波包变换的特性可知，某一时间段内信号的总能量等于各分段能量之和，设

式中，0<p_r<1，且1。

则定义分解尺度q的小波包节点细节系数能谱熵为

由以上分析可知，含有噪声的超声波信号的细节系数能谱熵会增大。因此确定最优小波包基分解的细节系数阈值时，可以把细节系数节点分为若干个子信带，计算每个子信带的能谱熵，选取熵最大的子信带，认为该子信带是噪声分布最集中的区域，将该子信带小波系数模的中值作为当前节点噪声方差，然后根据式（4-8）计算阈值。

（3）激光熔覆层超声波信号消噪方法 最优小波包基自适应阈值消噪算法如下：

1）选择sym8小波母函数，确定小波包分解的层数j，然后对超声波信号进行j层小波包分解。

2）采用前述的最优小波包基搜索算法找到信号分解的最优小波包基。

3）对最优小波包基分解得到的细节系数进行小波包能谱熵自适应阈值量化。

4）用非线性函数，将小波包能谱熵自适应阈值λ_j以上的小波包系数减去阈值后保留下来。

5）用第j层的近似系数和降噪处理过的最优小波包基各节点的细节系数重建信号。

（4）实验结果及分析 气孔是激光熔覆层内部常见的缺陷之一，在熔覆层内部采用电火花打孔方式加工出直径为3.5mm的横通孔模拟气孔缺陷（见图4-10），采用XZU-1型数字超声波检测仪，中心频率为5MHz的纵波探头对熔覆层试样内部通孔缺陷进行检测，采样频率为100MHz。

检测结果如图4-11所示。由图4-11a可知，现场采样到的信号中含有大量噪声。根据实际经验，缺陷信号比噪声信号具有更大的低频带宽，在低频范围内具有较高的信噪比，其时频分布沿着高尺度方向具有较强的能量延伸，因此从图中可以清楚地看到缺陷波位于始波和底面回波之间。根据缺陷回波的幅值以及在时基轴上的位置，结合距离波幅当量曲线（如AVG曲线）可以推断缺陷的当量尺寸以及埋藏深度。由于噪声的影响，图4-11a中缺陷回波的轮廓边缘不清晰，不利于缺陷定位、定量分析特征值的提取，因此采用sym8最优小波包基信号消噪方法对现场采集到的超声信号进行处理，分析结果如图4-11b、c、d、e所示。四种方法（阈值不同）的信噪比和均方差见表4-2。由图4-11及信噪比和均方差计算结果可以看出，最优小波分包能谱熵自适应阈值消噪效果优于其他消噪方法。从图4-11e中测量缺陷回波的幅值（62mV），缺陷回波在时基轴上的位置（17mm处）。检测结果表明，缺陷的埋藏深度与预制人工孔的实际位置误差为4.5%，当量尺寸与人工孔的实际尺寸误差为6.8%；其余三种方法的缺陷定量分析误差都在8%左右，而没有经过消噪处理的检测信号缺陷定量分析误差在15%左右。因此。采用最优小波分包能谱熵自适应阈值（Bwpesea）消噪方法对超声波信号进行处理，噪声消除比较彻底，能够获得表征缺陷当量尺寸、埋藏深度更为可靠的信息，提高了材料内部缺陷定量分析的准确度。

图4-10 Fe314激光熔覆试样

表4-2 Fe314激光熔覆层试样超声检测信号消噪统计结果