应用（3-1）式建立的超声检测模型预测激光熔覆再制造零件中缺陷的回波信号，还需要确定检测系统影响因子B（f）（影响因素如图3-12所示），这里采用超声检测系统分析法确定B（f）。图3-5所示的脉冲反射法超声检测系统，在适当的假设条件下，系统中各个组成部分都可以模拟成一个线性非时变系统（见图3-13），每个线性非时变系统的属性分别由时域中的单位冲击响应函数（上侧）和频域中单位冲击响应函数的频谱（下侧）来表征。由此可见，由脉冲发生器产生的输入电压信号s_i（t），经过一系列信号转化过程，最终得到超声检测仪示波器上显示的输出电压信号s_o（t）。这个过程在时域中可表示为

s_o（t）=s_i（t）b₁（t）m（t）c₁（t）e₁（t）r₁（t）h（t）h₁（t）e₁（t）c₁（t）m（t）b₁（t）（3-35）

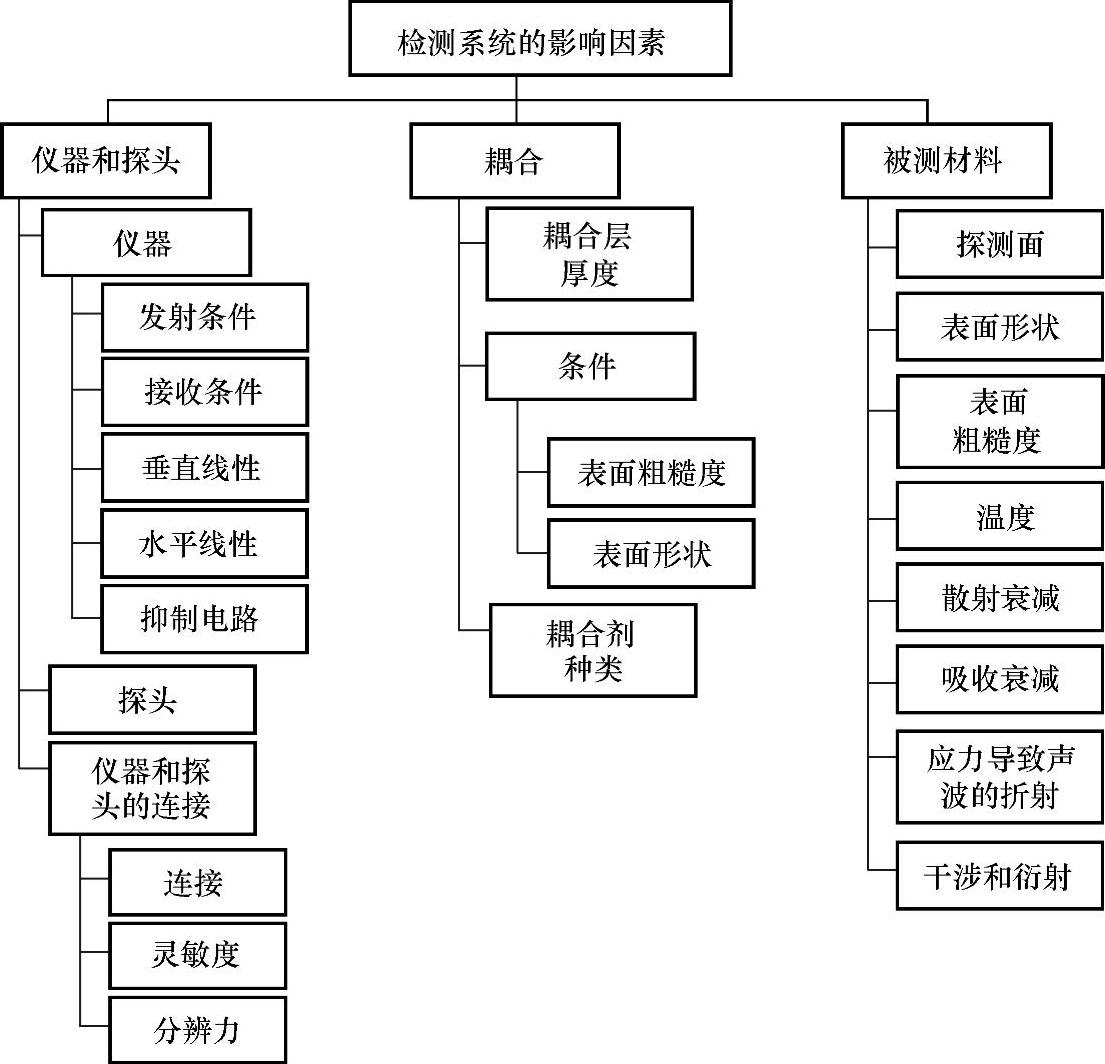
图3-12 超声检测系统的影响因素

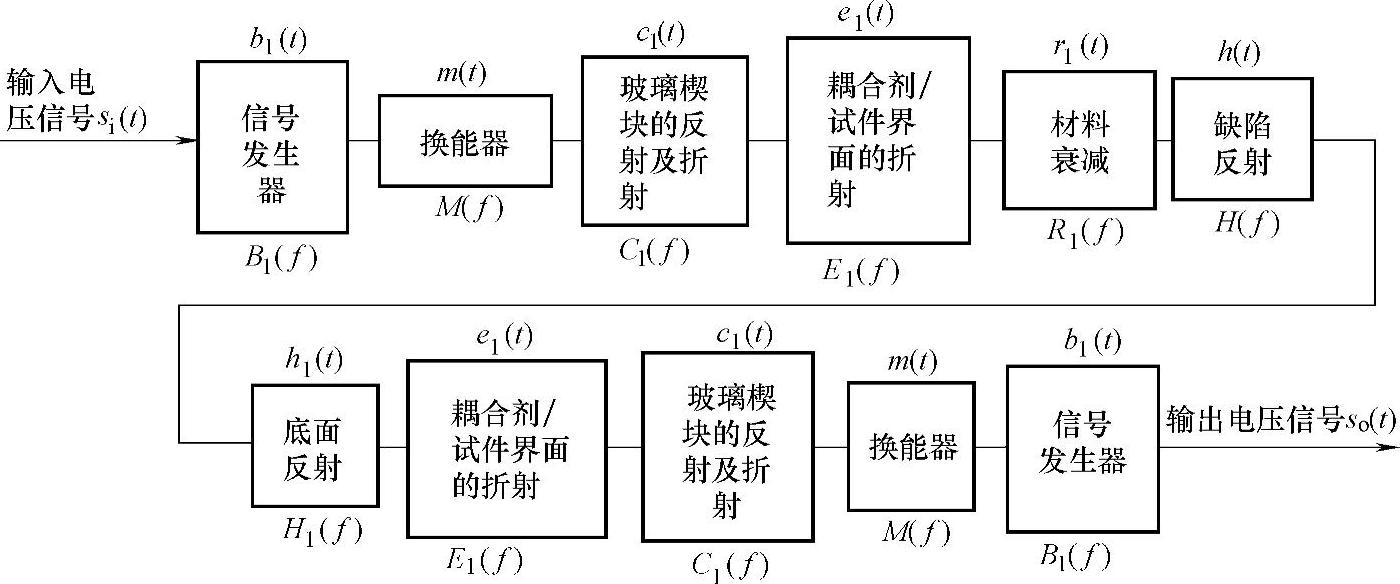
图3-13 一系列线性非时变系统组成的超声检测系统

在频域可表示为

S_o（f）=S_i（f）B₁（f）M（f）C₁（f）E₁（f）R₁（f）H（f）H₁（f）E₁（f）C₁（f）M（f）B₁（f）

（3-36）

因此，最终超声检测仪示波器上显示的输出电压信号，包含除了输入信号、缺陷回波信号、底波信号之外其他不相关系统的影响。这些影响有的取决于脉冲发生器、接收器和超声换能器的参数设定，有的取决于被检测材料的性质以及耦合剂的种类、厚度等。所以建立超声检测模型预测激光熔覆再制造零件中缺陷的回波信号，必须将这些因素考虑进去。可以将这些因素统称为检测系统的影响因子B（f）。

由式（3-36）可知，B（f）可表示为

B（f）=B₁（f）M（f）C₁（f）E₁（f）R₁（f）E₁（f）C₁（f）M（f）B₁（f） （3-37）

本书建立的超声检测模型见式（3-1），其声场计算采用瑞利积分结合pencil法，并考虑了超声波在熔覆层及基体材料中传播导致的振幅衰减见式（3-16），因此，式（3-37）中的材料衰减环节R₁（f）可以不考虑。采用有机玻璃楔块能够获得很好的耦合效果，因此忽略影响因素E₁（f）2。超声检测系统影响因子B（f）可以表示为

B（f）=B₁（f）M（f）C₁（f）C₁（f）M（f）B₁（f）=S_o（f）/S_i（f） （3-38）

式（3-38）表明，B（f）等于有机玻璃楔块底面的反射回波信号S_o（f）与信号发生器产生的输入信号S_i（f）之比。由于上述计算是在频域进行的，为了稳定频域相除过程，使用维纳滤波W（f）对频域相除结果进行处理，即(www.daowen.com)

图3-14所示为楔块底面反射的回波信号；图3-15所示为脉冲发生器产生的输入电压信号；图3-16所示为解卷积后求得的系统影响因子。

采用系统分析法确定系统的影响因子之后，根据式（3-1）计算探头接收到的缺陷回波信号在频域内的响应，然后通过傅里叶逆变换求得时域内的缺陷回波信号。图3-17、图3-18分别为激光熔覆再制造试样中裂纹、横通孔缺陷回波信号的数值计算和实验测量结果，从图中可以看出，数值计算结果和实验检测结果保持了很好的一致性，即缺陷回波的幅值、相位基本一致。从而验证了式（3-1）建立的各向异性激光熔覆再制造零件超声检测理论模型的准确性。另外，根据模型预测以及实验测量结果还可以判断出缺陷距离探头的距离（裂纹为52.6mm，横通孔位39.4mm），与缺陷的实际位置（裂纹为53mm，横通孔位40mm）基本吻合，误差仅为1%左右。

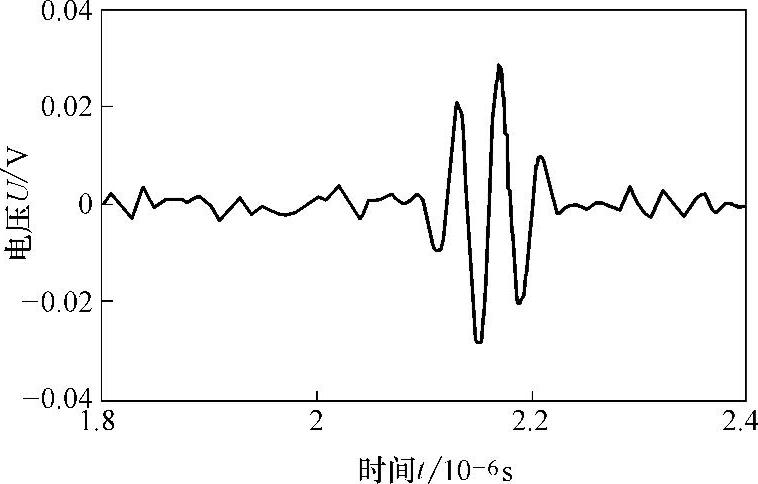
图3-14 楔块底面反射回波信号

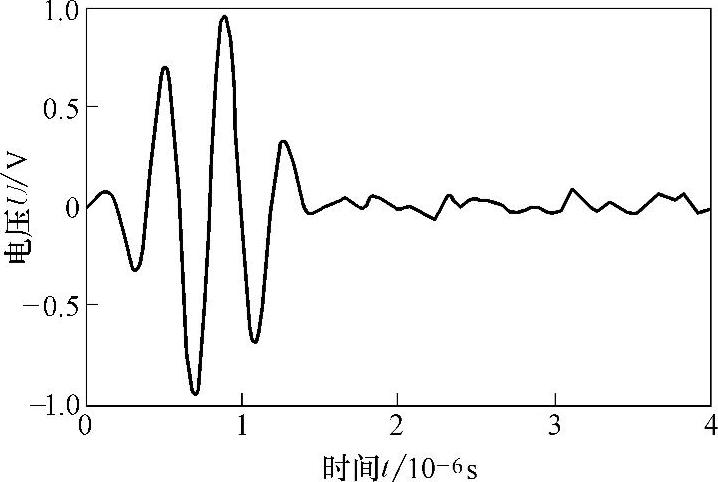
图3-15 脉冲发生器输入信号

图3-16 系统影响因子

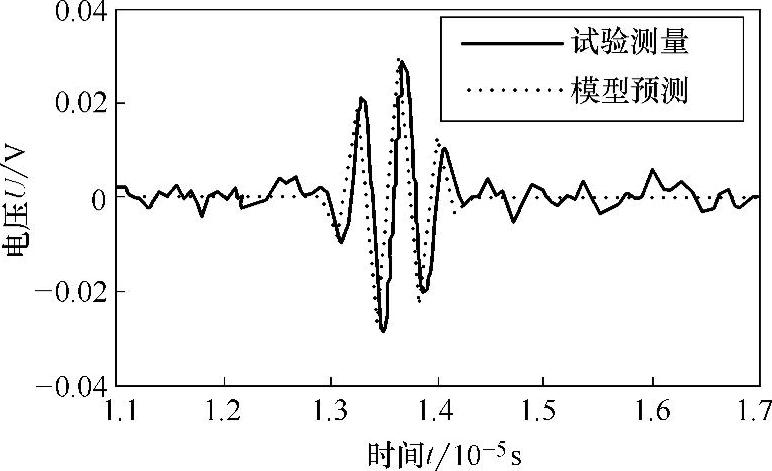
图3-17 直径6mm横通孔回波信号的模型预测与实验测量结果

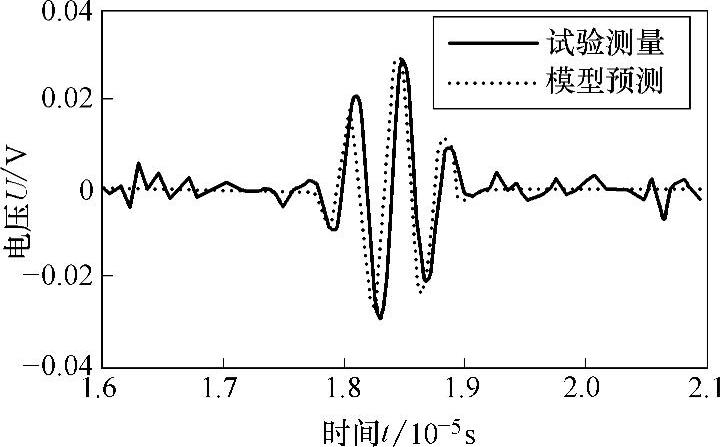
图3-18 长度为10mm裂纹回波信号的模型预测与实验测量结果