目前激光熔覆再制造零件中的缺陷主要归纳为两类，即面积型缺陷（未熔合和裂纹等）和体积型缺陷（气孔、夹杂物等），由于缺陷结构的复杂性，为了提高模拟的精度和计算效率，本书采用半解析法建立各类缺陷远场散射模型。

1.体积型及裂纹缺陷散射模型

基尔霍夫近似^[114]忽略沿缺陷表面传播的瑞利波的二次衍射项，将散射场用缺陷上每个点的切平面的反射声场的叠加近似代替。该理论用于处理各种体积型（气孔）缺陷和裂纹类缺陷。

以图3-10所示缺陷为例，S为声波发射源，从r′点处观察，观察角度为θ，入射角为β，当入射场u^I（r）入射到缺陷表面时，声束到达的区域称为亮区，标记为s+，声束无法到达的区域称为暗区，标记为s-。入射场和散射场的位移之和即为r′点处的位移场，即u^T（r′）=u^I（r′）+u^S（r′），根据弹性定理的格林公式，缺陷散射场沿p方向的分量可以表示为

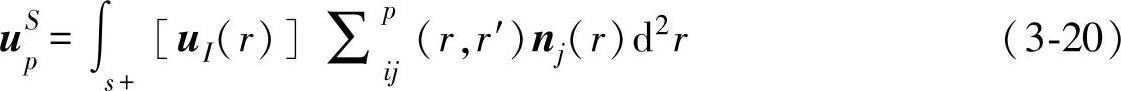
式中，[u_I（r）]为缺陷亮区面和暗区面的位移差；∑^p_ij（r，r′）表示点r处的发射点源在观察点r′处产生的p方向位移场分量；n_j表示亮区面的外法线方向。

入射场已知，求出u_I（r）和∑^p_ij（r，r′）两项表达式的值，即可得到观察点处的声场。

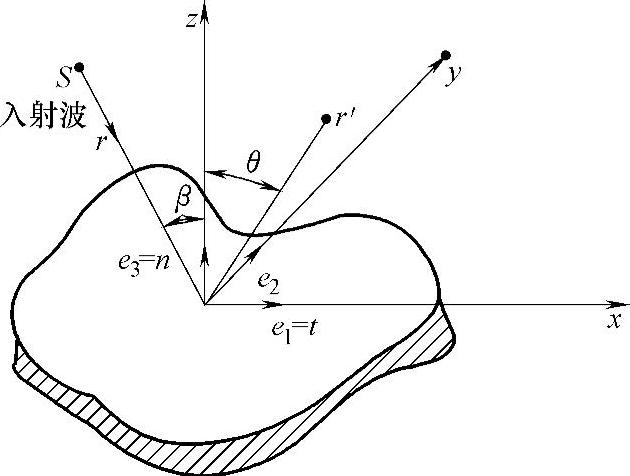
图3-10 缺陷散射示意图

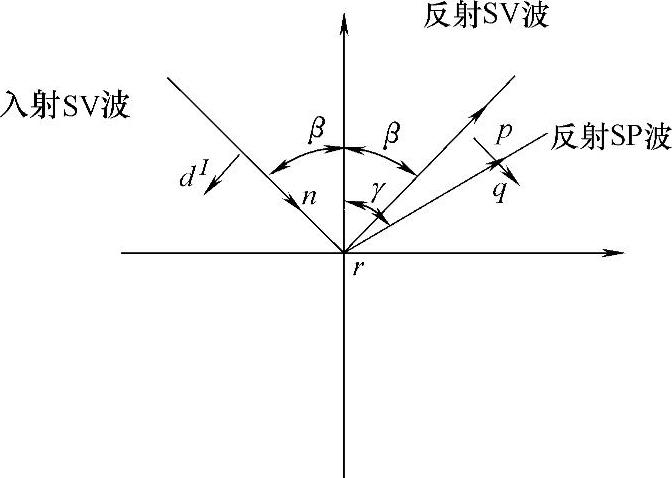
图3-11 入射波反射示意图

首先求解u_I（r），如图3-11所示，当横波SV以β角入射时，根据斯内尔定律，横波入射角β和纵波反射角γ满足以下关系

sinβv_l=sinγv_t （3-21）

根据基尔霍夫近似理论，缺陷上亮区和暗区的位移表达式为

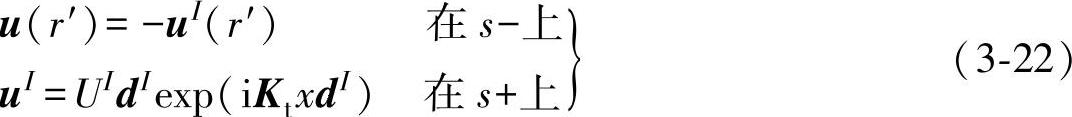
式中，K_t为横波波矢；U^I为最大位移幅值；d^I为入射横波的质点偏振方向，则反射位移场

u^R=U^I[A_ss（β）pexp（iK_txp）+A_sp（β）qexp（iK_txq）] （3-23）

式中，p、q分别为反射横波和反射纵波的质点偏振方向；A_ss、A_sp分别为横波反射系数和纵波反射系数，其表达式为

因此，u_I（r）可以表示为

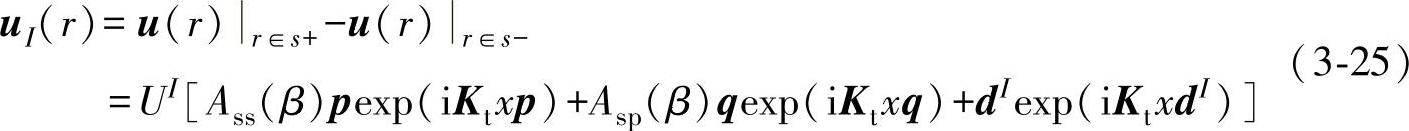
推导出缺陷亮区面和暗区面的位移差u_I（r）的求解表达式之后，还需要推导点r处的发射点源在观察点r′处产生的p方向位移场分量∑^p_ij（r，r′）的表达式。

式中，K_l为纵波波矢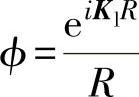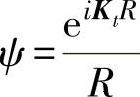；；；R=r-r′≈R₀-x₁sinθ-x₃cosθ。(www.daowen.com)

对于纵波入射和纵波反射，将u_I（r）各分量代入式（3-26），得到如下表达式

（3-27）

以势函数表示散射声场

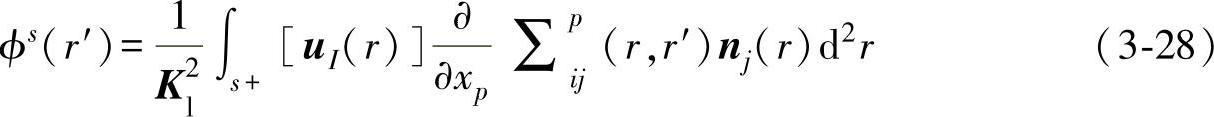
纵波入射引起的质点法向和切向振动位移分量分别为

将式（3-29）及式（3-27）代入式（3-28），得到缺陷散射场的表达式为

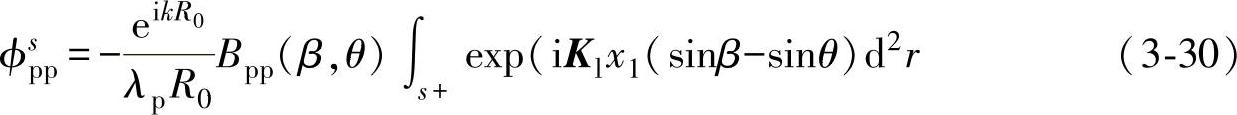
式中，λ_p为纵波波长，B_pp（β，θ）为散射系数，其表达式为

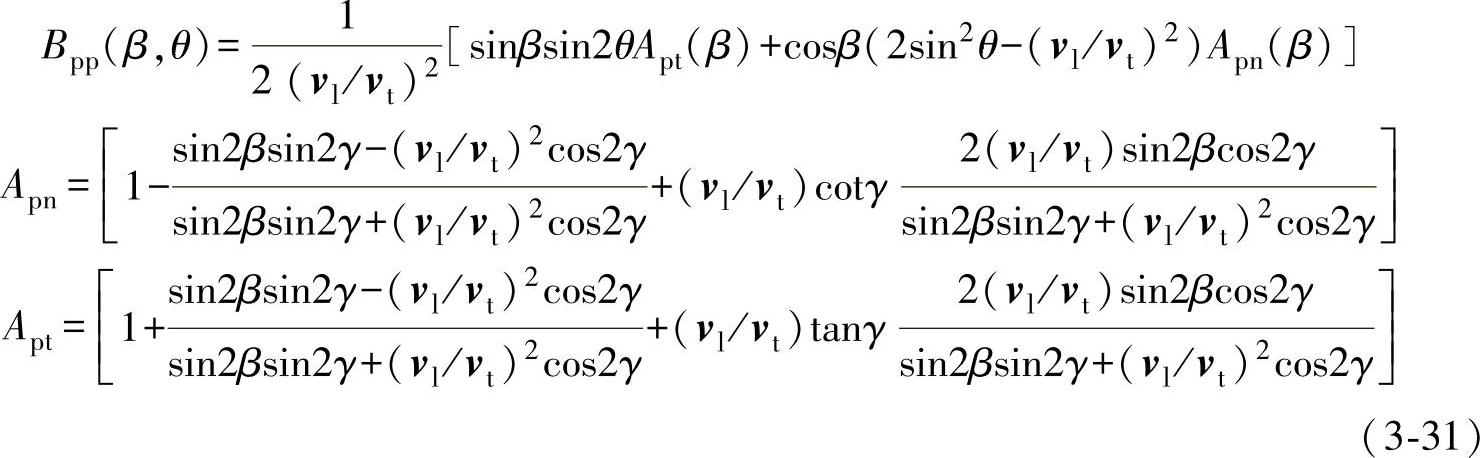
同样的方法，可以推导出纵波入射横波散射、横波入射纵波散射和横波入射横波散射的散射场和散射系数。

2.夹杂物缺陷散射模型

基尔霍夫近似散射模型可用于计算超声检测中尺寸较大的体积型和面积型缺陷，基尔霍夫近似是基于高频近似，对于尺寸小于1mm的夹杂物缺陷，误差比较大，因此引入基于低频近似的波恩近似理论来建立声场与夹杂物缺陷相互作用的数学模型。超声散射问题通常是采用偏微分方程来描述，波恩近似理论^[150]用量子力学中的积分方程代替偏微分方程，求解积分方程时采用精确迭代法，得到级数形式的渐进解。波恩近似把无限级数的第一项作为近似解，也就是将散射体内的未知位移场用入射场来代替，从而求得纵波与横波的散射振幅表达式为

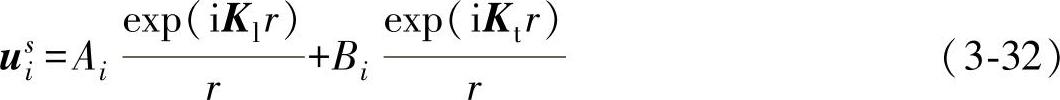
式中，A_i、B_i为纵波和横波散射场的振幅；K_l、K_t为纵波波矢和横波波矢。

当纵波入射时，A_i、B_i的表达式为

横波入射时，A_i、B_i表达式为

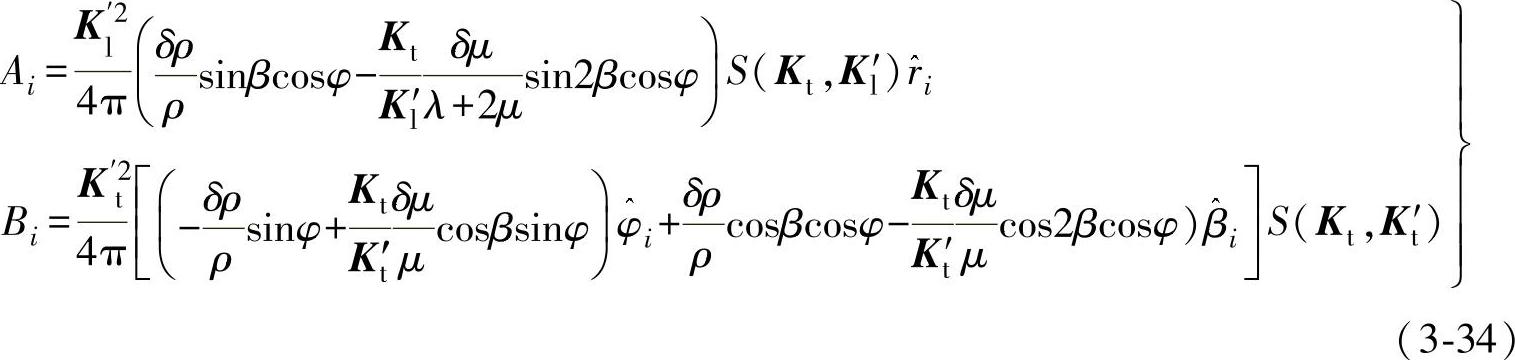
式中，S（K_l，K_l′）为形状因子；λ、μ、ρ分别为材料的弹性常数和密度，δλ、δμ、δρ分别为介质与缺陷弹性常数和密度差值；β、φ分别为入射角和散射角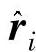，表示沿r方向的单位矢量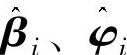，表示沿着入射角度和散射角度方向的单位矢量。

波恩近似建立的模型是显式表达式，且不需要对缺陷进行网格划分，因此很容易编程计算。