1.瑞利积分法（Rayleigh Integration Method，RIM）

瑞利积分法^[148]的基本思想是将探头离散成一系列点源，这些离散的点源在空间中任一点产生声压的叠加即为该点的声压计算值。利用瑞利积分法计算声场时，很多学者通常采用与其他方法或模型（如边界衍射法、pencil法、驻相法等方法）相结合的方式来计算探头的发射声场及在各种介质中的传播，此处选择瑞利积分和pencil法建立声场计算模型，该模型计算效率高，可用于处理任意探头（直探头、斜探头和相控阵等）、任意界面（曲面、不规则界面）、复杂材质（多层各向异性）等情况。计算探头在半无限大空间的发射声场时，将探头晶片离散成一系列点源，点源的响应可以用格林函数G（r_T，r）表示，将其代入亥姆霍兹方程得到

▽²G（r_T，r）+k²G（r_T，r）=-4πδ（r_T-r） （3-2）

式中，k为波数；δ（r_T-r）是狄拉克脉冲函数。

当求解得到点源声场之后，任意点源产生的场可以表示为

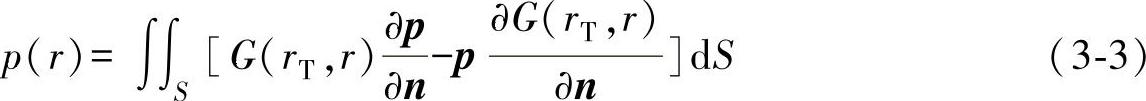
式（3-3）式称为基尔霍夫公式，表示声压p（r）可以由包含点r的一个闭合曲面上的声压和声压的法向微分进行积分得到。

对于自由空间的点声源，格林函数为

在闭合面法向求导

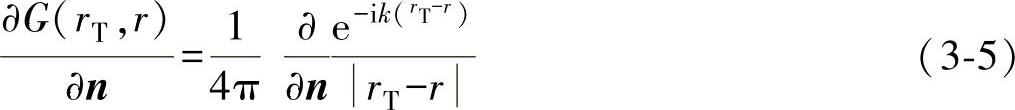
根据声压和质点速度间关系

将式（3-4）～式（3-6）带入式（3-3），得到空间中任意一点的声压为

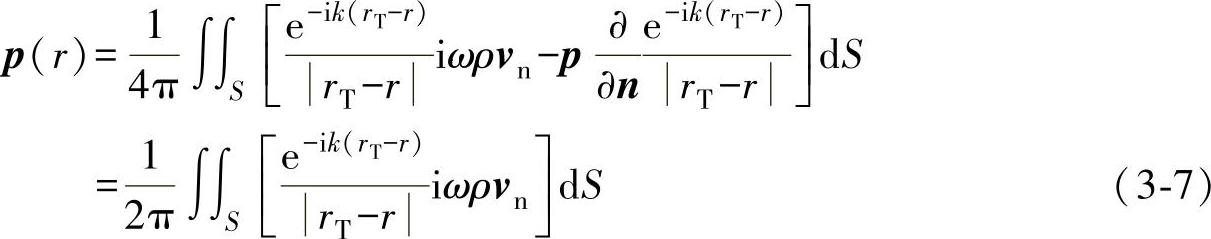
式（3-7）即为瑞利积分表达式，它可以看作是惠更斯原理的一种表示方法，即每个点源dS的声场响应叠加起来可以表示面积为S的面源发射声场。

空间中任意点速度势的瑞利积分表达式为

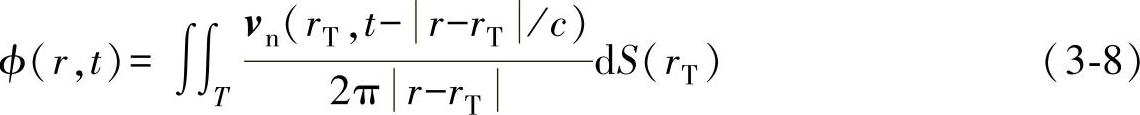
式中，ϕ（r，t）为耦合介质中点r在时刻t的速度势；T表示探头；v_n为探头表面点源在时刻t的振动速度；r_T为探头表面的点源位置；|r-r_T|为从点源到计算点r处的距离；|r-r_T|/c为声波从点源处传播到计算点处的时间；dS（r_T）为探头点源r_T的面积。

2.pencil法

在弹性固体介质中，当计算点距离点源足够远时，可以近似认为计算点处的声波是平面波，平面波在传播过程中随着距离的增加振幅会不断减小。pencil^[148]法主要应用于计算点源发射的波在传播过程中的振幅衰减，记为D_F。如图3-6所示，pencil法是点源发射的一束射线，在传播过程中会产生发散，振幅衰减D_F可以用pencil的截面积S和固体角Ω求得

D_F^-2=dΩ/dS （3-9）

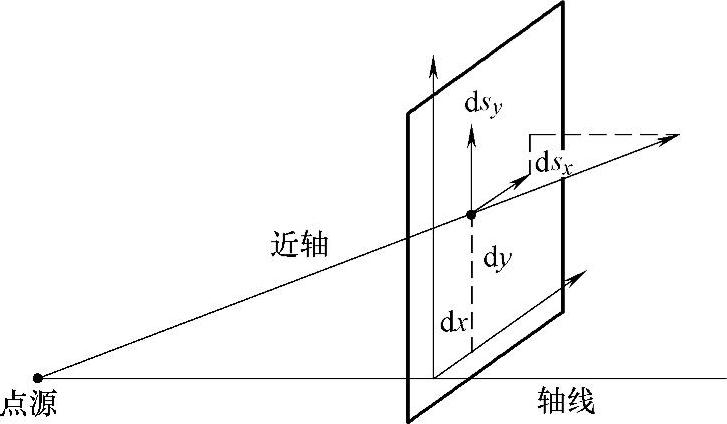
为了计算截面积S和固体角Ω，首先用声束矢量ψ（dx，dy，ds_x，ds_y）来描述声束的传播方向及其近轴，如图3-7所示。其中，dx、dy表示平面波在轴线上的位置；ds_x、ds_y表示近轴声线的慢度矢量在波阵面上的投影。ψ（0，0，ds_x，ds_y）为点源处的声束矢量，ψ′（dx′，dy′，ds_x′，ds_y′）为计算点处的声束矢量，两者之间通过声束传播矩阵L_i关联起来

式中，A、B、C、D为2×2矩阵。

若将pencil的截面积和固定角分别表示为dS=dx′dy′，dΩ=ds_xds_y/S²，振幅衰减D_F可以由声束传播矩阵得到

D_F^-2=S²detB （3-11）

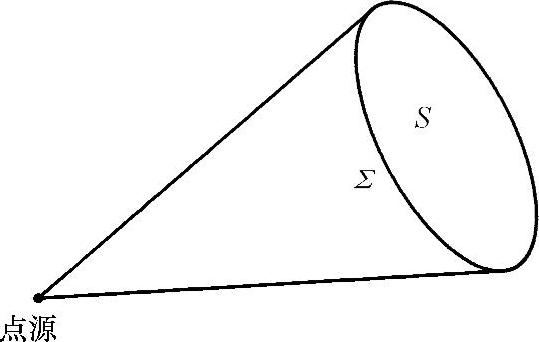
图3-6 点源声束发散示意图

(www.daowen.com)

图3-7 点源发散声束的矢量描述

对于不同介质，传播矩阵L_i不同，各向同性介质的声束矢量为

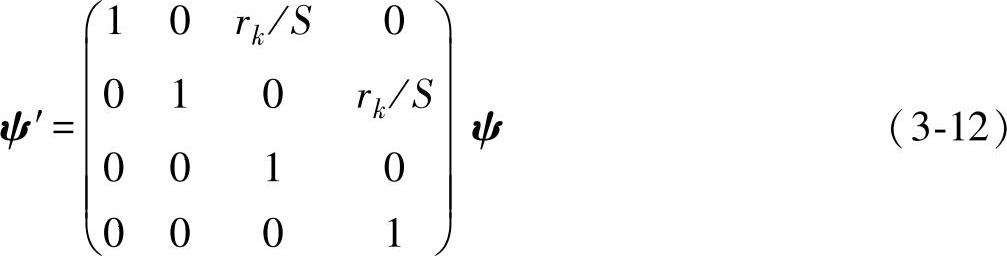
各向异性介质的声束矢量为

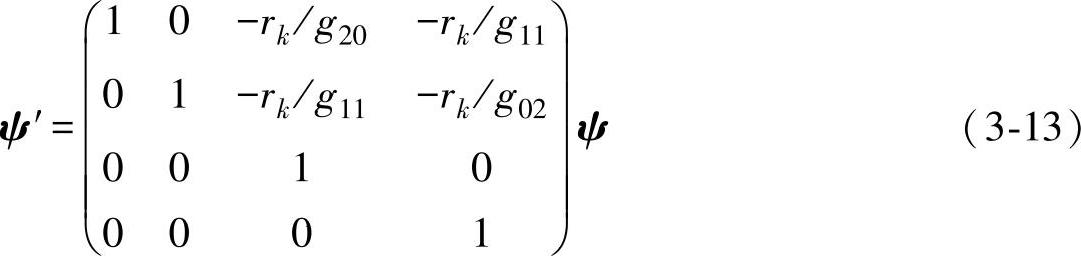
式中，r_k表示沿声束矢量方向的传播距离；g_mn（m、n=0，1，2）的表达式如下

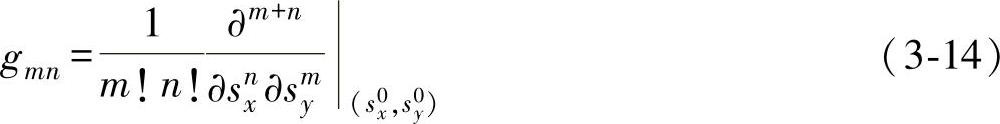
式中，s⁰_x、s_y⁰表示轴线上的慢度分量。

采用pencil法计算复杂结构中任意两点间的关系时，可以通过迭代法求解。由于激光熔覆层通常为多层堆积熔覆形成的非均质各向异性组织，单层厚度比较小（0.2～2.5mm），因此每一层可近似为均质各向异性，因此激光熔覆层中超声波的传播问题就转化为多层均质各向异性介质中的超声波传播问题，计算激光熔覆层中声场时，传播矩阵可以由均匀区域的传播矩阵迭代相乘得到，最后计算偏离因子和声场。

ψ′=Lψ=L₁L₂…L_nψ （3-15）

式中，L₁，L₂，…，L_n表示声波传播过程中所遇到的各个均匀区域的传播矩阵。

采用瑞利积分结合pencil法计算固体中任意一点的声势时，首先计算离散点源在该点处产生的声势的叠加，其次考虑每个点源到计算点的衰减和在界面处的折射，因此需要引入振幅衰减D_F和折射系数T_S对式（3-8）进行修正，即可得到固体中点r的声势

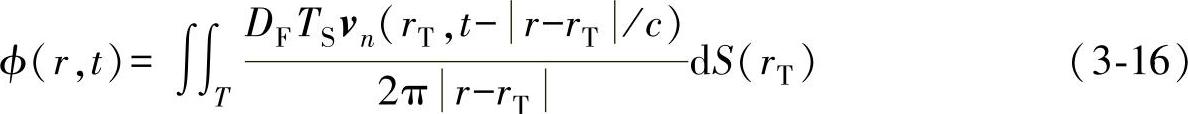
瑞利积分结合pencil法声场计算原理如图3-8所示。具体应用该声场计算模型计算各向异性激光熔覆层中声场时，需要确定材料的慢度值。材料的各向异性对入射声场的影响程度与慢度值^[148]有关。通过求解克里斯托弗尔方程可以得到材料的慢度值并绘制出慢度曲线图，慢度曲线的法向量决定着声束的偏转方向，慢度曲线的曲率决定着声束的聚焦和散焦特点。求解克里斯托弗尔方程还需要了解材料的晶系及表征材料弹性性质的劲度系数矩阵。Fe314激光熔覆材料为多晶立方晶系，其劲度系数矩阵^[149]如下

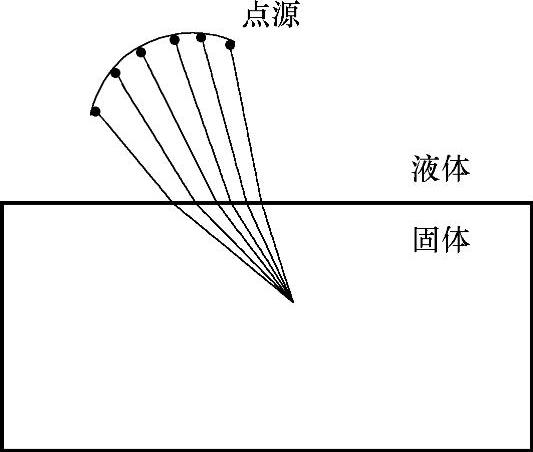
图3-8 瑞利积分结合pencil法声场计算原理图

其中，c₁₁=27.7，c₁₂=0，c₄₄=8.2，单位为10¹⁰N/m²。立方晶系的克里斯托弗尔方程为

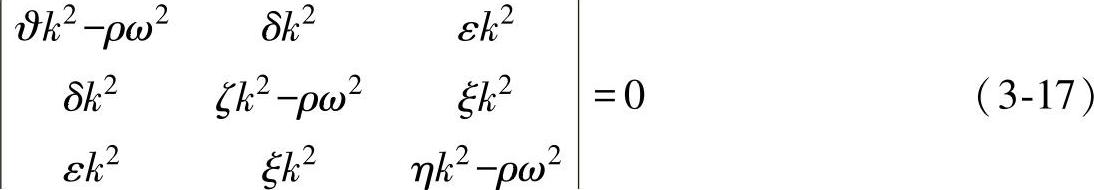
式中，ρ为材料密度，Fe314激光熔覆材料的密度为7770kg/m³；ω为圆频率；k为波数；ϑ、ζ、η、δ、ε、ξ在不同晶系中不尽相同，立方晶系中各参数表达式如下：

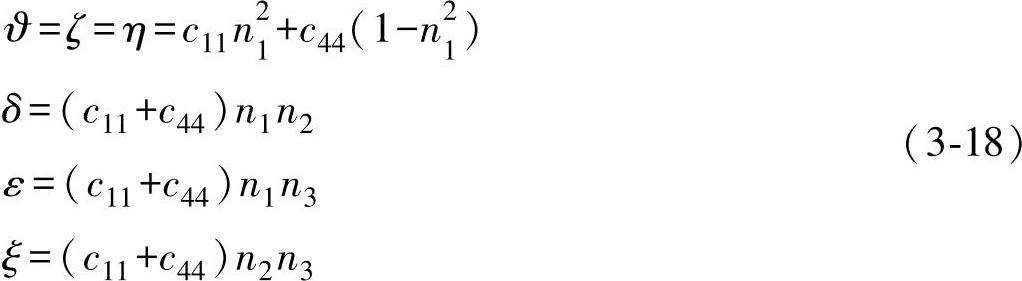
式中，n₁、n₂、n₃分别为传播方向在x、y、z轴上的角度余弦值，即

式中，k_x、k_y、k_z分别为波数k在x、y、z方向的分量。求解克里斯托弗尔方程得到三个s（s²=k²/ω²）值，s即为各向异性Fe314激光熔覆材料的慢度值。计算得到的慢度面在Oxy、Oyz、Ozx坐标平面上的界面如图3-9所示，可以看到，传播方向不同时，声速差别较大。

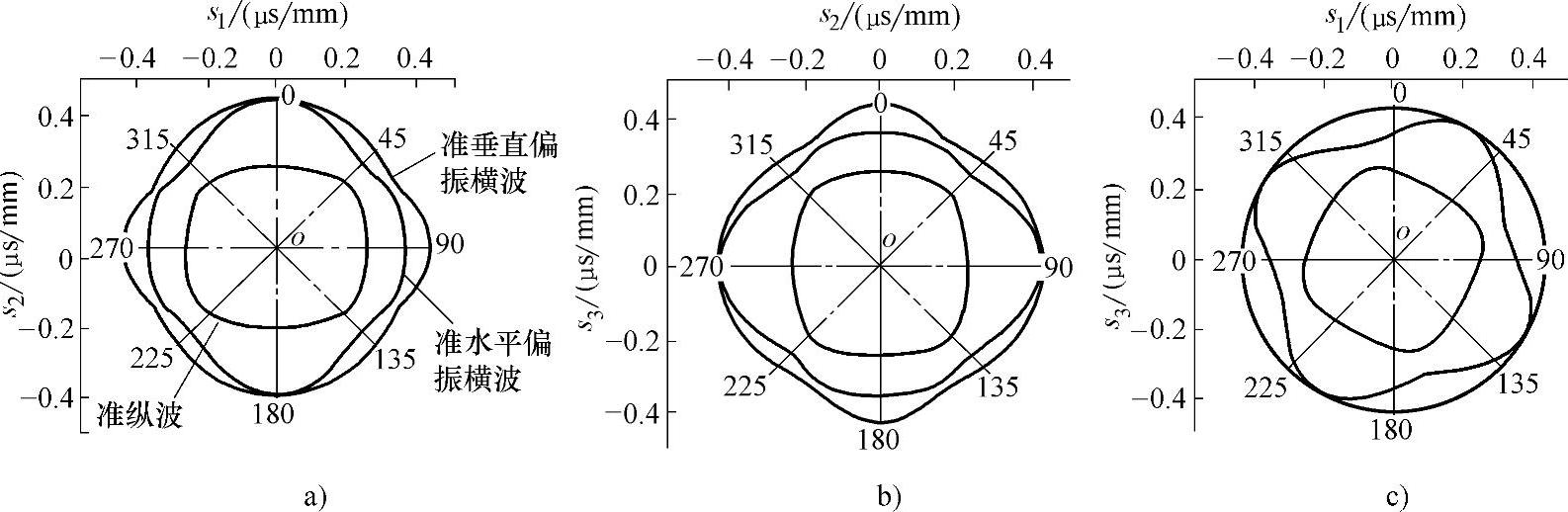
图3-9 Fe314合金激光熔覆材料的慢度图

a）Oxy面 b）Oyz平面 c）Oxz平面

超声波在各向异性激光熔覆层中传播时，遇到界面所产生的反射和折射现象均符合斯内尔定律，即入射相速度、反射相速度和折射相速度位于同一平面内，入射声束、反射声束和投射声束的慢度在界面上的投影值相等。