超声检测主要是通过分析探头接收到的缺陷和结构散射声场来评定被检物，因此准确计算缺陷与结构的散射声场是超声检测数值模拟的关键。当用超声波检测材料内部缺陷时，内部缺陷相当于不均匀区域，根据超声波遇到不均匀区域的散射特性，反过来确定这个区的状态，如形状、大小、位置等，称为逆散射问题。不均匀区域是怎样散射超声的，称为正散射问题。要解决逆散射问题，首先应当解决正散射问题，因此深入了解超声波在固体中的散射现象，是超声检测技术应用的前提和基础。相比于流体，固体中超声波传播的现象更复杂，主要原因是，固体中不仅存在各向异性，而且固体内存在纵波、横波，并且两者之间可以进行模式转换。在固体表面，有沿着表面传播的表面波（也称瑞利波）。当固体材料某个方向的尺寸特别小时，体内声波能量将会集中导向这个方向，从而在材料内形成波导，波导内存在导波（由纵波和横波多次反射和相互转换得到的综合体）。因此，深入研究超声波在固体中的传播和散射现象，可以为检测的定性、定量化开辟道路。

由于碳素钢中常见的缺陷主要有孔洞（包括气孔）、裂纹和夹杂物等，因此本书主要研究这几类缺陷的散射声场特征。

1.孔洞类缺陷散射声场

数值模拟的材料对象选择碳素钢，从半无限区域取长为26mm，宽为30mm的二维计算区域，采用直径为2mm的圆孔模拟孔洞类缺陷，圆孔位于坐标（0，15）处。采用plane42单元进行剖分，材料弹性模量E=2×10¹¹Pa，泊松比G=0.3，密度ρ=7800kg/m³。上表面为自由表面，其余3个表面施加人工应力边界条件。激励载荷、时间步长及网格尺寸采用与前述相同的设置。

纵波入射时，声场快照如图2-10～图2-13所示。图2-10所示为激励的初始阶段，入射平面纵波I-P由上向下传播；图2-11中平面纵波遇到圆孔缺陷时，产生了背向反射的圆柱形纵波R-P，继续向下传播的纵波I-P沿着圆孔壁法线不断调整前进方向，也就是沿着孔壁向前爬行；在图2-12中，平面纵波I-P沿着孔壁继续爬行的同时产生波阵面为圆柱形的模式转换横波S，模式转换横波的波前与沿着孔壁爬行的平面纵波波前相连；图2-13中为绕过圆孔缺陷之后，各个波形将独立传播。图2-14所示为纵波入射时，光弹实验中观察到的圆孔形缺陷声场散射照片^[144]，各个波形分布及强弱分布与图2-13所示模拟结果具有很好的一致性。

在坐标（0，22）处模拟直径为14mm的换能器进行y方向扫描，图2-15为接收到的A扫描信号，由于模型下边界施加了人工应力边界，所以A扫描信号中没有出现底面回波信号，Y为始波（激励波）信号，F为缺陷回波信号。图2-16所示为（0，25）处接收到的y方向A扫描信号，从图2-15中可以看出，始波到达（0，25）处的时间为1.76μs，图2-16中始波到达（0，22）的时间为2.27μs，两处的距离为3mm，超声波（纵波）传播的时间延迟为0.51μs，代入公式v_l=Δl/Δt，计算碳素钢中超纵波的传播速度为v_l=5840m/s，与碳素钢中纵波的实际测量值（v_l=5890m/s）误差仅为0.85%，采用同样的方法可以计算出图2-15中缺陷与检测位置处的距离为6.94mm，与实际距离7mm基本吻合，误差仅为0.8%，因此采用有限元模拟超声波纵波对各向同性固体中孔洞类缺陷的检测是完全可行的，数值模拟结果是可靠的。

图2-10 t=2.4μs时刻的声场传播瞬态图

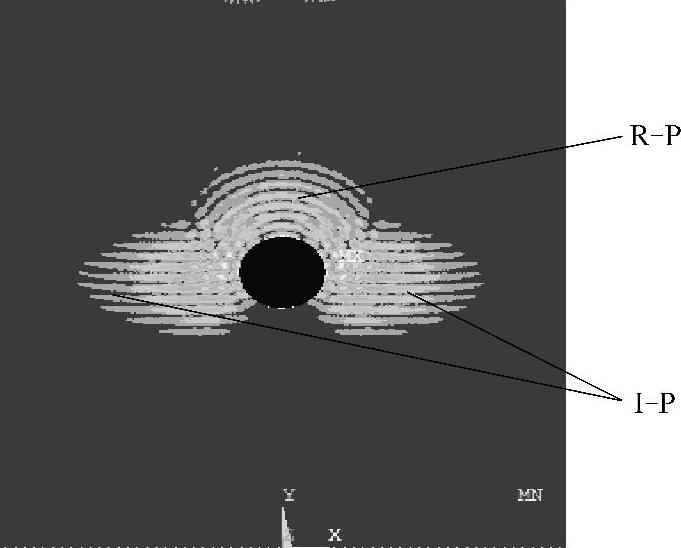
图2-11 t=2.8μs时刻的声场传播瞬态图

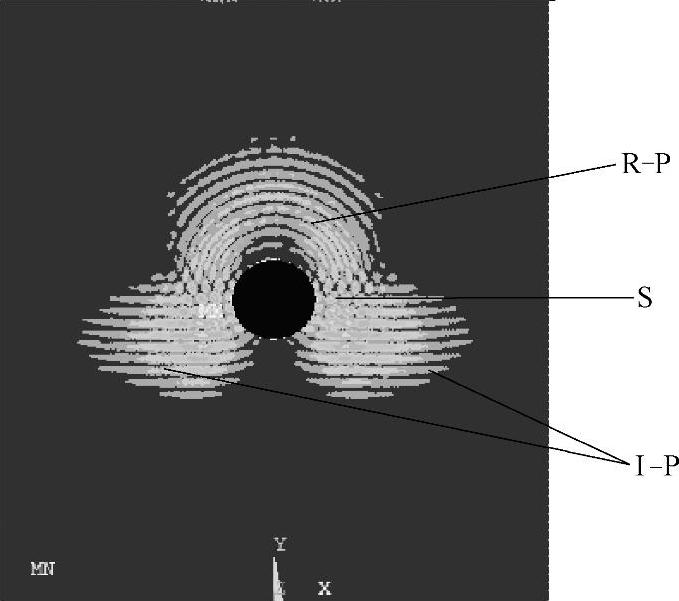
图2-12 t=3.3μs时刻的声场传播瞬态图

图2-13 t=4.4μs时刻的声场传播瞬态图

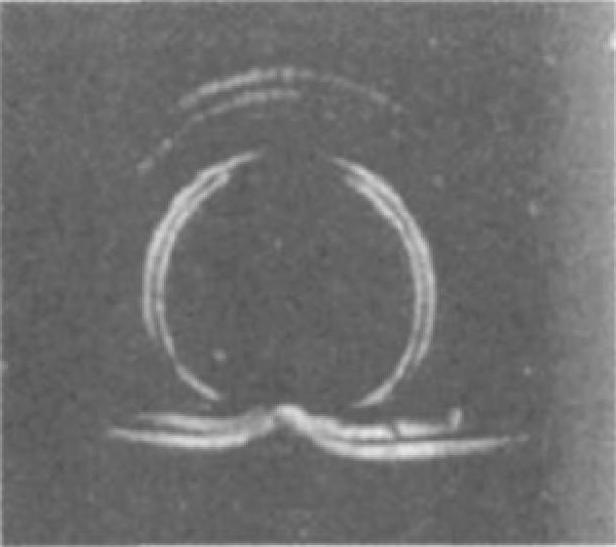
图2-14 光弹实验照片（纵波入射）

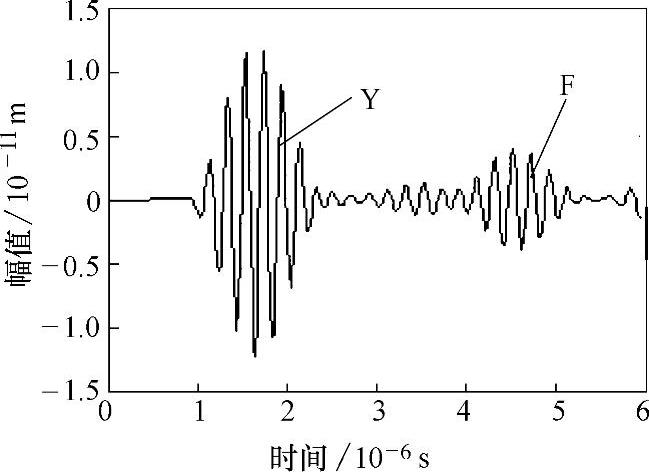
图2-15 y=25mm处的A扫描信号图

横波入射时，声场快照如图2-17～图2-19所示，图2-17中，入射平面横波I-S由上向下传播，遇到圆柱形孔缺陷时，产生了背向反射的圆柱形横波R-S，继续向下传播的横波I-S沿着圆孔壁法线不断调整前进方向，也就是沿着孔壁向前爬行；图2-18中，入射横波I-S沿着孔壁继续爬行的同时产生波阵面为圆柱形的模式转换纵波P，模式转换纵波的传播速度比横波快，其波前领先于沿着孔壁爬行的入射横波波前；图2-19中可以清晰地看到，由于横波的衰减很慢，横波爬过圆孔的最低点之后继续沿着孔壁爬行的情形。图2-20所示为横波入射时光弹实验中观察到的圆孔形缺陷声场散射照片^[144]，各个波形分布及强弱分布与图2-19所示模拟结果具有很好的一致性。

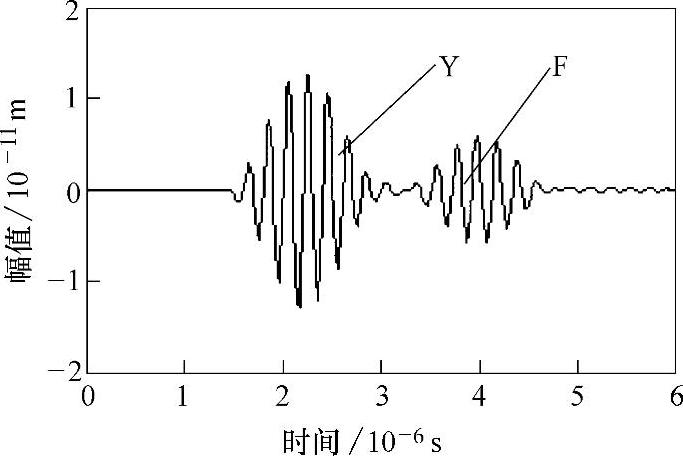
图2-16 y=22mm处的A扫描信号图

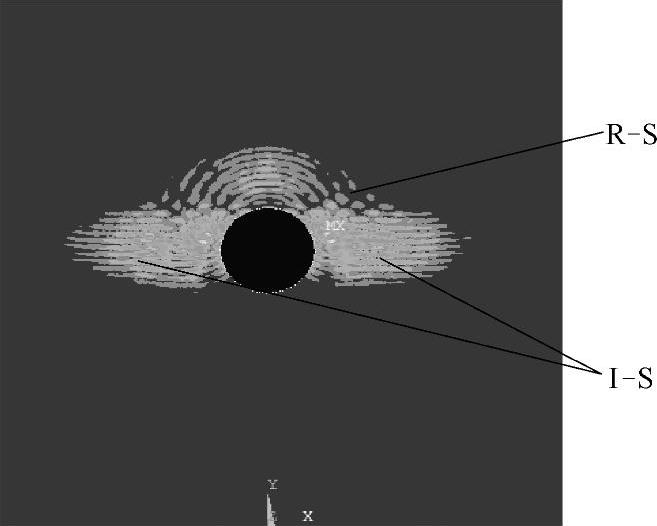
图2-17 t=4.4μs时刻的声场传播瞬态图

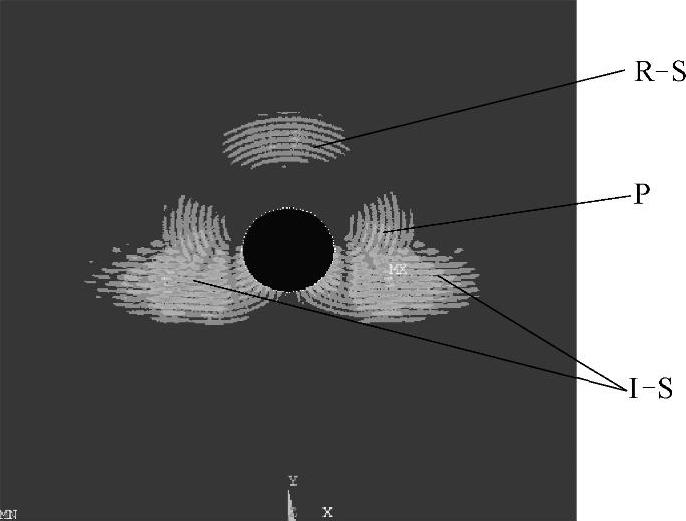
图2-18 t=5.1μs时刻的声场传播瞬态图

图2-19 t=6.1μs时刻的声场传播瞬态图

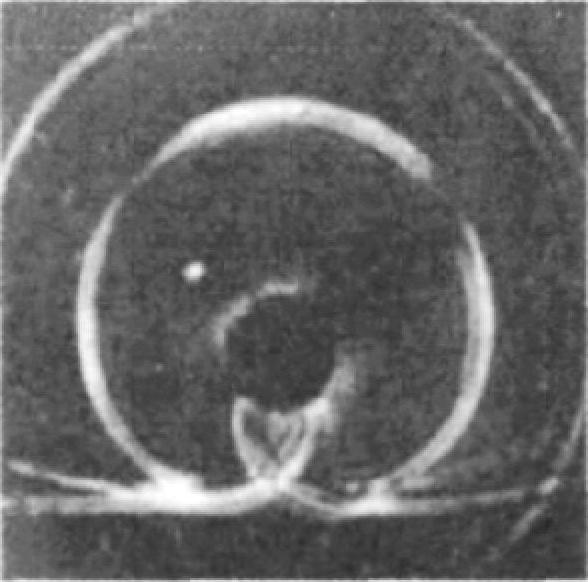
图2-20 光弹实验照片（横波入射）

关于圆孔形缺陷的超声波散射问题，Miklowitz等于1978年做了理论计算，计算结果表明，圆孔形缺陷的散射波会连续绕孔壁螺旋旋转。此后应崇福等人使用动态光弹实验方法首次证实了这一理论预计，实验中观察到脉冲平面横波入射时，散射横波绕孔壁的螺旋旋转“爬行”。但由于脉冲平面纵波入射时，绕孔壁的散射纵波衰减很快，光弹实验中没有清晰地观察到绕孔壁的螺旋旋转，因此采用数值模拟方法不仅弥补了实验的不足，同时也证实了Miklowitz理论预计的正确性。

在坐标（0，20）及（0，18）处模拟直径为14mm的换能器进行y方向扫描，图2-21、图2-22所示分别为两处接收到的y方向A扫描信号，Y为始波（激励波）信号，F为缺陷回波信号。从图2-21中可以看出，始波到达（0，20）处的时间为1.75μs，图2-22中始波到达（0，18）的时间为2.36μs，两处的距离为2mm，超声波（横波）传播的时间延迟为0.61μs，代入公式v_t=Δl/Δt，计算碳素钢中超横波的传播速度为v_t=3260m/s，与碳素钢中横波速度实际测量值（v_t=3230m/s）误差仅为0.9%，采用同样的方法可以计算出图2-21、图2-22中缺陷与检测位置处的距离与模型中实际距离基本吻合，误差仅为0.8%左右，因此采用有限元模拟超声波横波对各向同性固体中孔洞类缺陷的检测是完全可行的，数值模拟结果是可靠的。

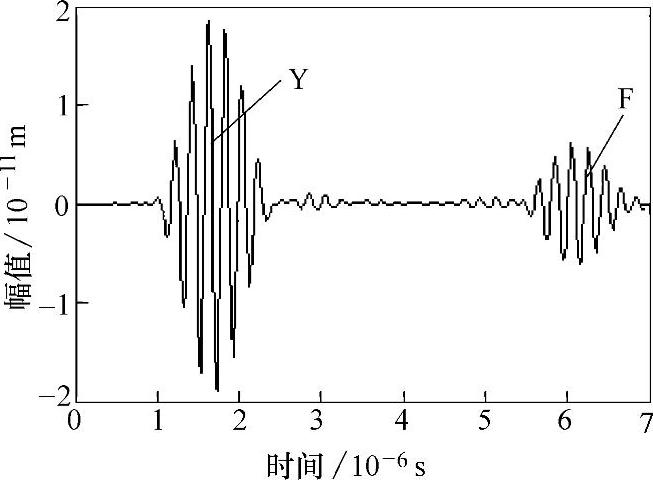
图2-21 y=20mm处的A扫描曲线图

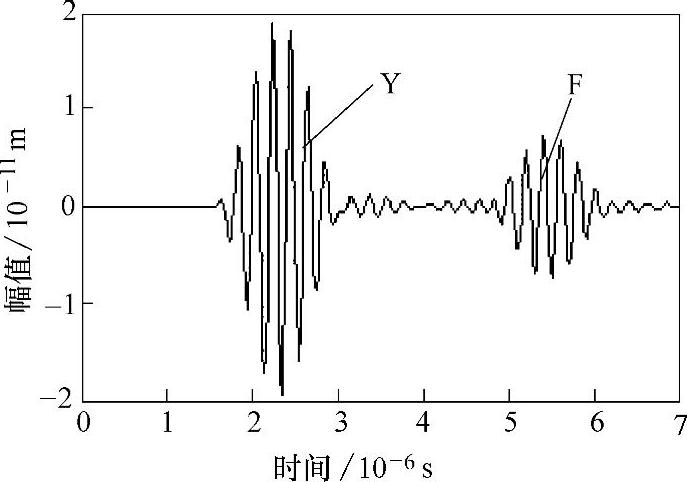
图2-22 y=18mm处的A扫描曲线图

2.裂纹类缺陷散射声场

数值模拟的材料对象仍然为碳素钢，从半无限区域取长为32mm、宽为30mm的二维计算区域，采用长为8mm、宽为2mm的矩形模拟裂纹类缺陷，裂纹中心位于坐标（13，10）处。裂纹平行于材料表面，采用plane42单元进行剖分，下表面为自由表面，其余3个表面施加人工应力边界条件。激励载荷、时间步长及网格尺寸采用与前述相同的设置。

纵波垂直于裂纹方向入射时，模拟结果如图2-23～图2-26所示，图2-23中入射平面纵波I-P由下向上传播。图2-24中，当平面纵波遇到垂直于超声波传播方向的裂纹缺陷时，在裂纹两端的尖端处散射出了波前为圆柱形的纵波脉冲Y-P和横波脉冲Y-S以及沿着裂纹的上下表面传播的表面瑞利波脉冲B-B，通常将裂纹尖端处散射出的波形统称为衍射波；在衍射波产生的同时，在裂纹的下表面产生了背向反射平面纵波R-P，从图2-24可以看出，在裂纹散射产生的各种波形中，背向反射平面纵波的能量最大，因此，这种情况下，采用脉冲反射法检测效果更好。图2-25中，绕过裂纹缺陷之后，各个散射波形将独立传播。图2-26所示为t=4μs的声场传播瞬态图，由于横波脉冲Y-S能量比较弱，此时，已经看不到Y-S波的传播，只看到表面瑞利波B-B、背向反射平面纵波R-P和纵波脉冲Y-P的传播。

图2-23 t=1.4μs时刻的声场传播瞬态图

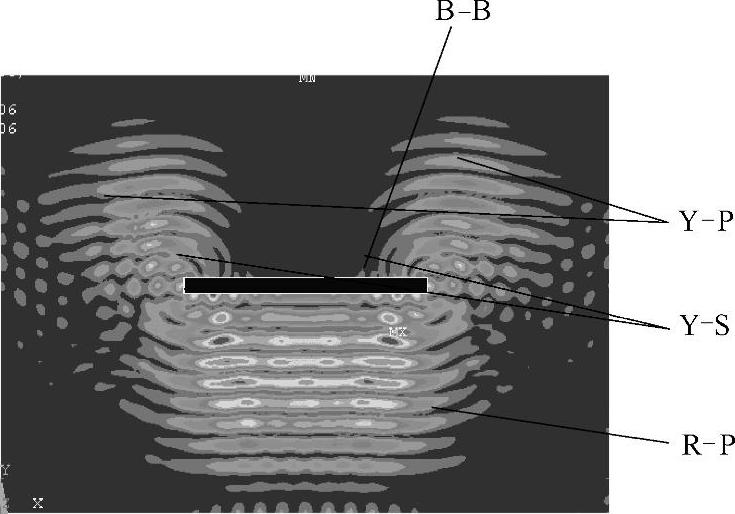
图2-24 t=2.9μs时刻的声场传播瞬态图

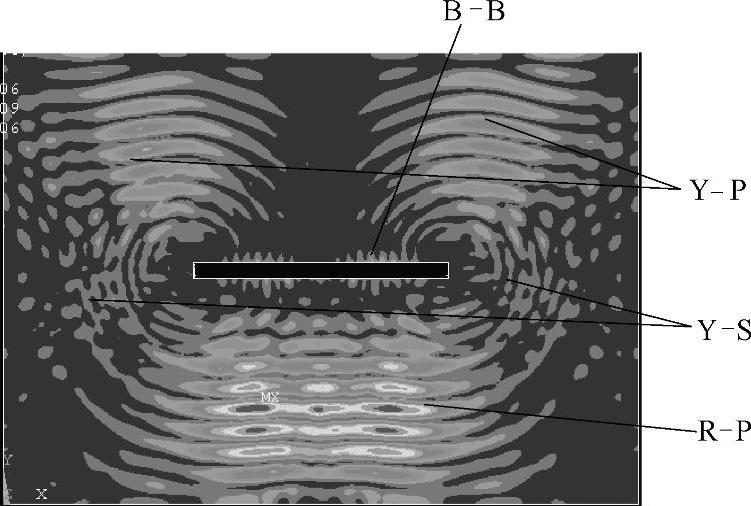
图2-25 t=3.4μs时刻的声场传播瞬态图

图2-26 t=4μs时刻的声场传播瞬态图

纵波入射方向与裂纹呈30°时，模拟结果如图2-27～图2-29所示（计算参数的设置与裂纹呈水平分布时相同），图2-27中，入射平面纵波首先遇到裂纹的第一个尖端，瞬间散射出波前为圆柱形的纵波脉冲Y-P和横波脉冲Y-S，以及沿着裂纹上下表面传播的表面瑞利波脉冲B-B，在衍射波产生的同时，在裂纹的下表面产生了与裂纹倾斜方向一致的背向反射平面纵波R-P；图2-28中，入射平面纵波遇到裂纹的第二个尖端时，瞬间再次散射出波前为圆柱形的纵波脉冲Y-P和横波脉冲Y-S，以及沿着裂纹上下表面传播的表面瑞利波脉冲B-B，从图2-28中可以看出，第二个尖端散射出的各个波形的能量明显小于第一个尖端散射出各波形的能量，尤其是横波脉冲的能量非常微弱，纵观所有散射波形，背向反射平面纵波R-P能量最高，因此，这种情况下，采用脉冲反射法检测仍是上佳选择。对比纵波入射方向与裂纹垂直或倾斜两种情况下超声波散射过程可知，散射波波形没有发生变化，但是各个波形的能量分布、传播方向发生了变化。(www.daowen.com)

应崇福等人采用动态光弹技术^[144]观察到了透明玻璃材料内部长的有限宽平面薄缝的散射过程，实验中观察到的现象与上述数值模拟结果完全吻合，但是采用实验手段只能观察透明材料内部超声波的传播和散射过程，工程实际应用中，绝大多数零件都是采用不透明的金属材料制造的，因此，数值模拟的优越性不言而喻。

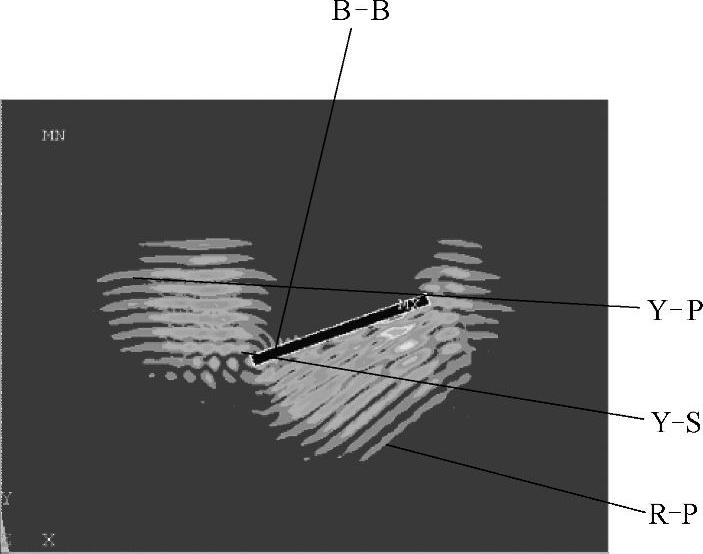
图2-27 t=3.3μs时刻的声场传播瞬态图

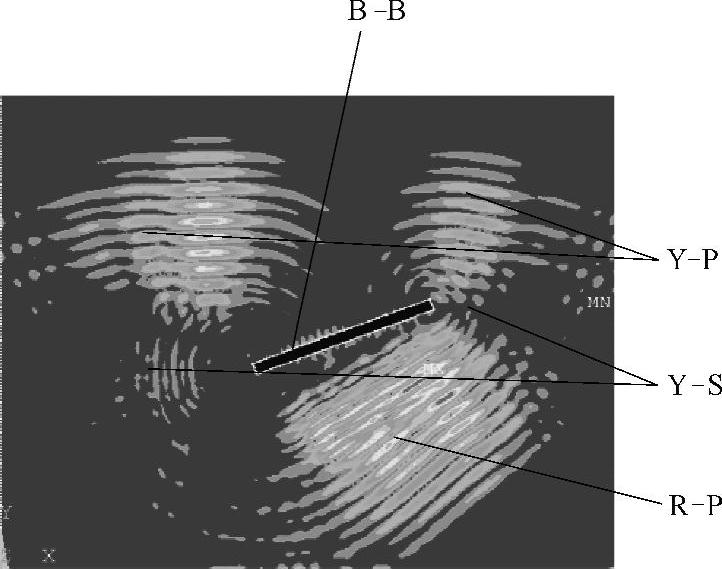
图2-28 t=3.9μs时刻的声场传播瞬态图

图2-30所示为入射纵波垂直于裂纹情况下，坐标（16，5）处接收到的y方向A扫描信号，图2-31所示为入射纵波与裂纹角度为30°时，坐标（16，8）处接收到的y方向A扫描信号。其中Y为始波（激励波）信号，F为缺陷回波信号。结合孔洞类缺陷的数值模拟结果可以看出，虽然两类缺陷的散射声场并不完全相同（波形的类别、能量分布、传播方向皆不同），但是两类缺陷的A扫描曲线形状差别却很小，因此根据A扫描曲线虽然可以清楚地判断出材料内部缺陷的存在以及缺陷与探头的直线距离（沿着声束传播方向），但很难分辨出缺陷的类型。采用与前述相同的方法可以计算出图2-30、图2-31中缺陷与检测位置处的距离与模型中实际距离基本吻合，误差仅为0.84%左右，并且可以计算出纵波的传播速度为v_l=5846m/s，与碳素钢中纵波的实际测量值（v_l=5890m/s）误差仅为0.82%，因此采用有限元模拟超声波纵波对各向同性固体中裂纹类缺陷的检测是完全可行的，数值模拟结果是可靠的。

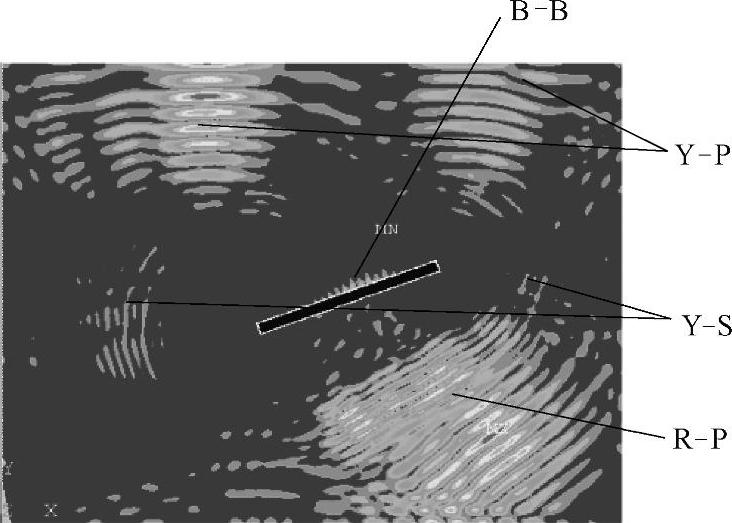
图2-29 t=4.7μs时刻的声场传播瞬态图

3.夹杂物缺陷散射声场

钢的夹杂物主要来源于两方面：一是冶炼过程中产生的，主要包括浇注过程中钢液和空气的二次脱氧物以及出钢时加入铁合金的脱氧产物，这类夹杂物颗粒一般比较细小，在钢中分布均匀；二是冶炼过程中，从外界代入的，此类夹杂物尺寸比较大，而且形状复杂，在钢中分布不均匀，破坏了金属本体的连续性，对钢的危害很大。

钢中的夹杂物主要有四类：第一类为氧化物：Al₂O₃、SiO₂、FeO等；第二类为硫化物：FeS、MnS等；第三类为氮化物：AlN、Si₃N₄等，硫化物、氮化物是使钢材产生裂纹的主要原因；第四类为硅酸盐夹杂物：Fe₂SiO₄、Mn₂SiO₄、FeO·Al₂O₃·SiO₂。

将碳素钢中夹杂物形状分别简化为矩形和五边形，选择Al₂O₃及MnS两种夹杂物的材料参数进行数值模拟分析，具体参数见表2-1。从半无限区域取长为26mm、宽为20mm的二维计算区域，Al₂O₃夹杂物长2mm、宽1.5mm，夹杂物中心位于坐标（0，10）处。采用plane42单元进行剖分，上表面为自由表面，其余3个表面施加人工应力边界条件。激励载荷、时间步长及网格尺寸采用与前述相同的设置。

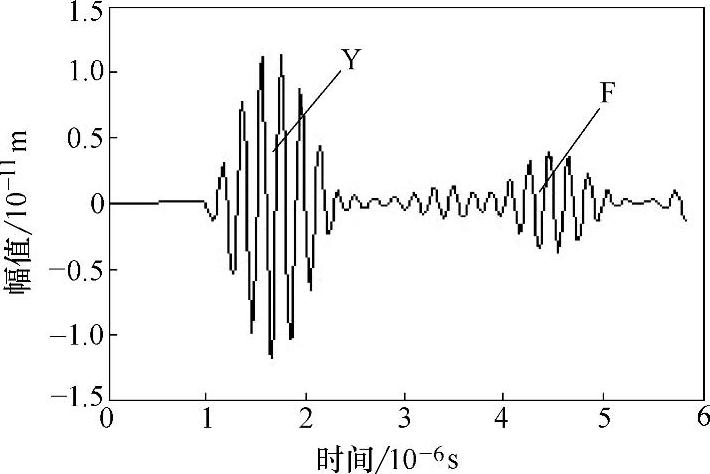
图2-30 y=5mm处的A扫描曲线图

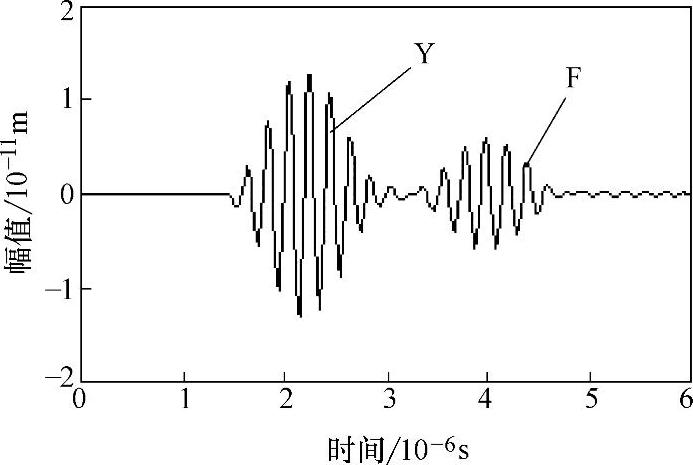
图2-31 y=8mm处的A扫描曲线图

表2-1 材料力学性能参数

纵波垂直入射时，模拟结果如图2-32～图2-35所示，图2-32中入射平面纵波由上向下传播。图2-33中，当平面纵波遇到夹杂表面时，由于基体材料和夹杂物材料的力学性能参数（弹性模量、泊松比以及密度）不同，就会发生反射和折射，入射平面纵波被分成两翼绕射矩形夹杂，在夹杂的表面不断发生反射和折射，由于入射波垂直于夹杂表面，反射波为纵波，折射波也为纵波。从图2-33可以看出，折射到夹杂物中的超声波波前为直线形，其传播速度略大于基体中入射平面纵波的传播速度。图2-34中，当夹杂物中的折射波传播到夹杂和基体材料的接触面时，再次发生反射和折射，折射波入射到基体材料中，波前仍然为直线形，与此同时，射矩形夹杂的两翼入射波也在沿着入射方向传播。图2-35中，入射平面纵波和折射波经过夹杂散射之后，原来的一束声波被散射成多束声波，背向入射声波方向的反射波能量较弱。

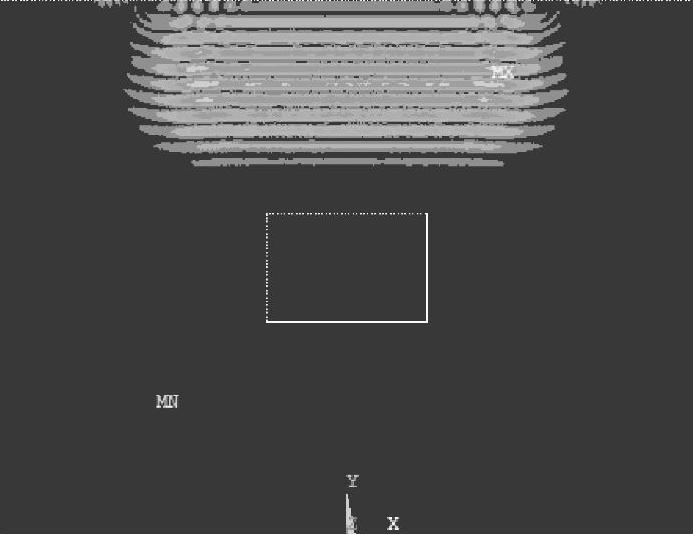
图2-32 t=1.3μs时刻的声场传播瞬态图

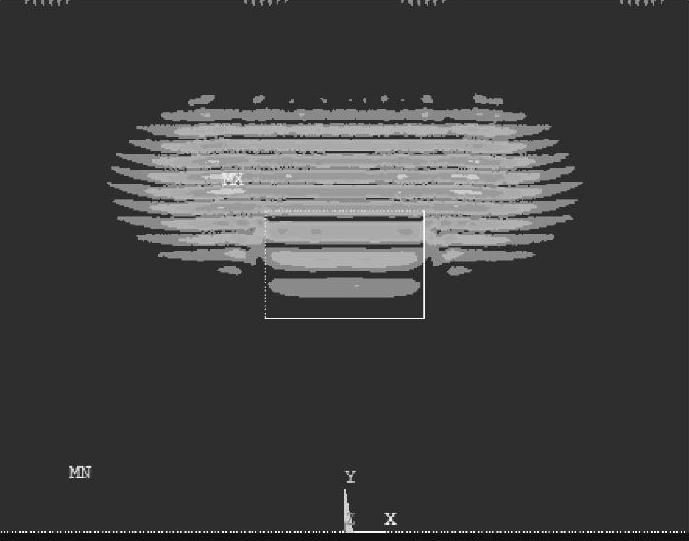
图2-33 t=2.1μs时刻的声场传播瞬态图

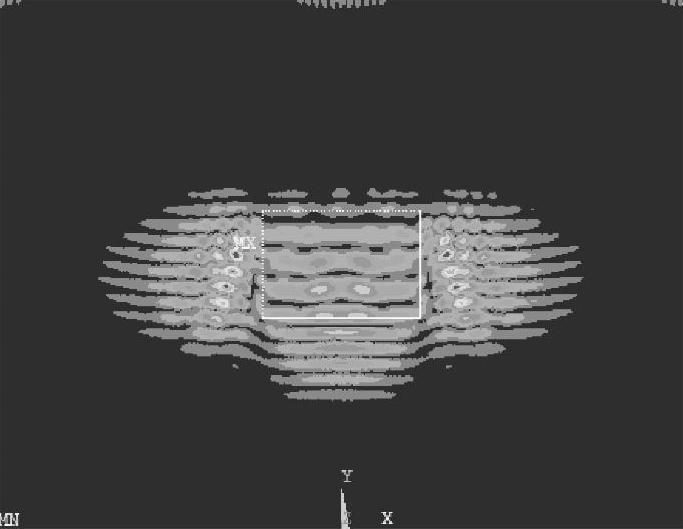
图2-34 t=2.7μs时刻的声场传播瞬态图

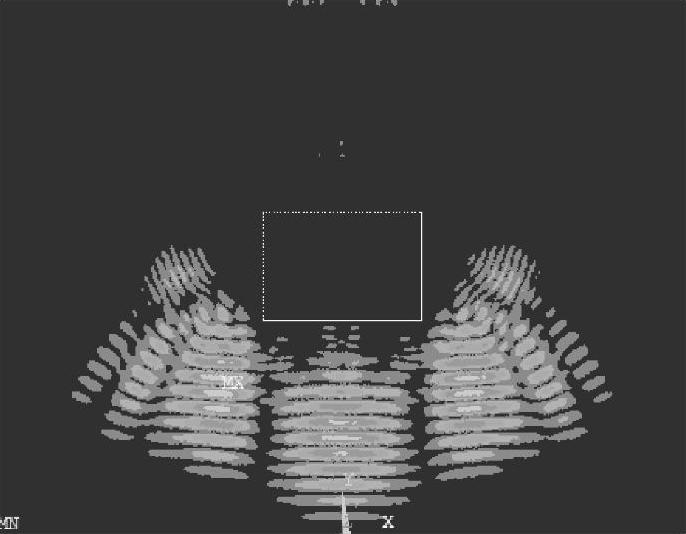
图2-35 t=3.5μs时刻的声场传播瞬态图

从半无限区域取长为26mm、宽为20mm的二维计算区域，MnS夹杂物形状为五边形（内接圆直径为2mm），夹杂物中心位于坐标（0，10）处。采用plane42单元进行剖分，上表面为自由表面，其余3个表面施加人工应力边界条件。激励载荷、时间步长及网格尺寸采用与前述相同的设置。

纵波垂直入射时，模拟结果如图2-36～图2-38所示，图2-36中，入射平面纵波由上向下传播，图2-37中，当平面纵波遇到夹杂表面时，由于基体材料和夹杂材料的力学性能参数（弹性模量、泊松比及密度）不同，就会发生反射和折射，由于入射波不垂直于夹杂物表面，反射波分为两种，即反射纵波、反射横波，折射波也分为两种，即折射纵波、折射横波。入射平面纵波绕射五边形夹杂物时，在夹杂物的表面不断发生反射和折射，从图2-37可以看出，折射到夹杂物中的超声波波前为圆柱形，其传播速度与基体中入射平面纵波的传播速度基本相等。图2-38中，当夹杂物中的折射波传播到夹杂物和基体材料的接触面时，再次发生反射和折射，折射波入射到基体材料中，波前仍然为圆柱形。图2-39中，入射平面纵波和折射波经过夹杂物散射之后，继续沿着原来的传播方向传播，背向入射声波方向的反射波能量较弱。

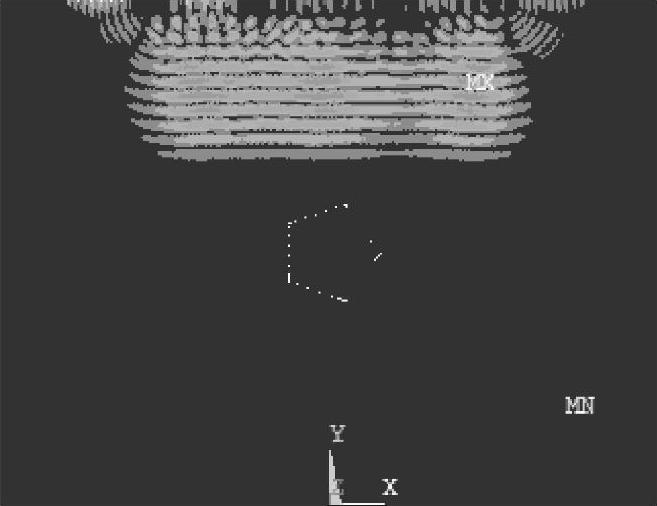
图2-36 t=1.5μs时刻的声场传播瞬态图

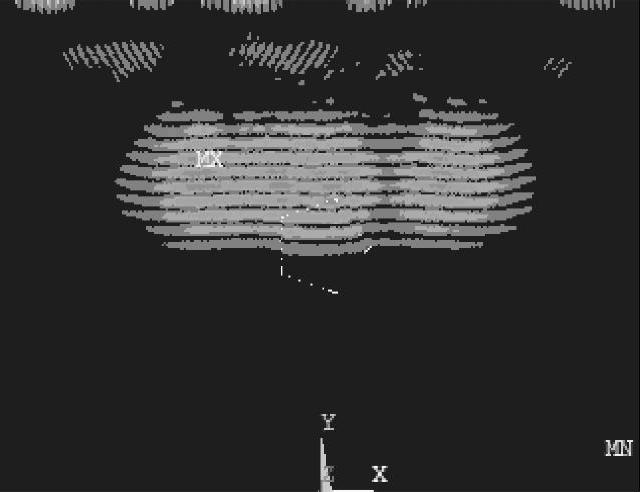
图2-37 t=2.1μs时刻的声场传播瞬态图

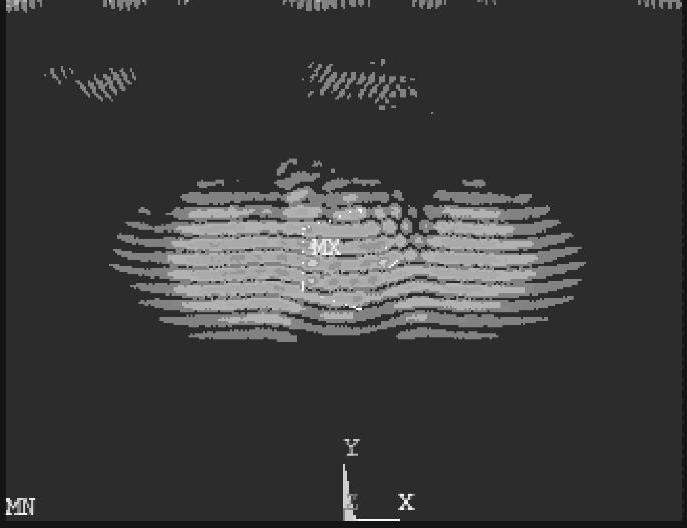
图2-38 t=2.6μs时刻的声场传播瞬态图

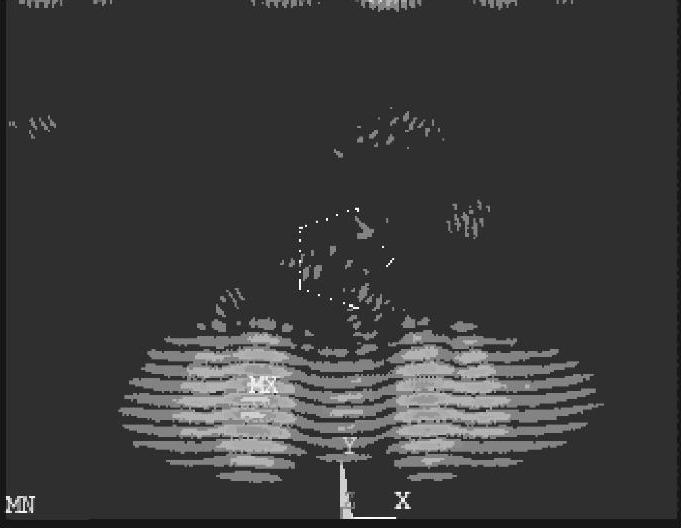
图2-39 t=3.6μs时刻的声场传播瞬态图

图2-40所示为MnS夹杂物计算模型中，坐标（0，15）处接收到的y方向A扫描信号。图2-41为Al₂O₃夹杂物计算模型中坐标（0，17）处接收到的y方向A扫描信号，图中Y为始波（激励波）信号，F为缺陷回波信号。结合上述声场快照分析可知，上述两种夹杂物属于体积型缺陷，界面反射率低，并且有相当一部分声波透过夹杂物进行传播，因此反射波能量较弱，所以相应的A扫描信号中，缺陷回波的幅值都比较小。图2-42所示为坐标（0，3）处接收到的经Al₂O₃夹杂物散射的超声波A扫描信号。图2-43所示为坐标（0，3）处接收到的经MnS夹杂物散射的超声波A扫描信号。相比于没有夹杂物情况下相同位置处接收到的超声波A扫描曲线（见图2-44），有夹杂时A扫描信号的幅值明显减小了（相差一个数量级）。因此，对于钢中这两类非金属夹杂物，由于夹杂物界面反射率比较低，特别是缺陷体积比较小时，采用折射法（双探头，一发一收分布在缺陷两侧）检测效果更好。

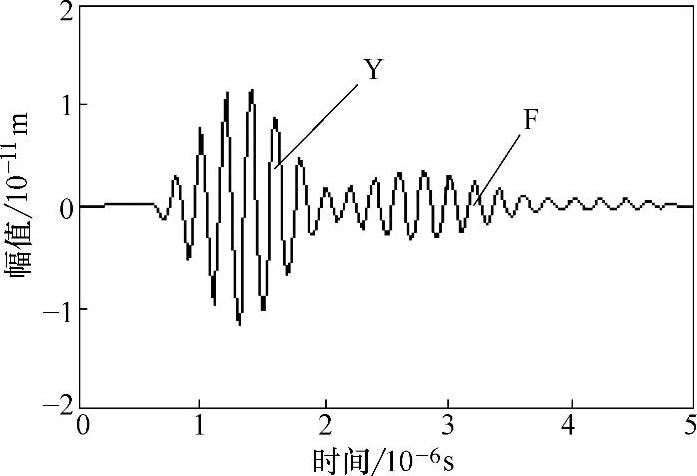
图2-40 y=15mm处的A扫描信号图

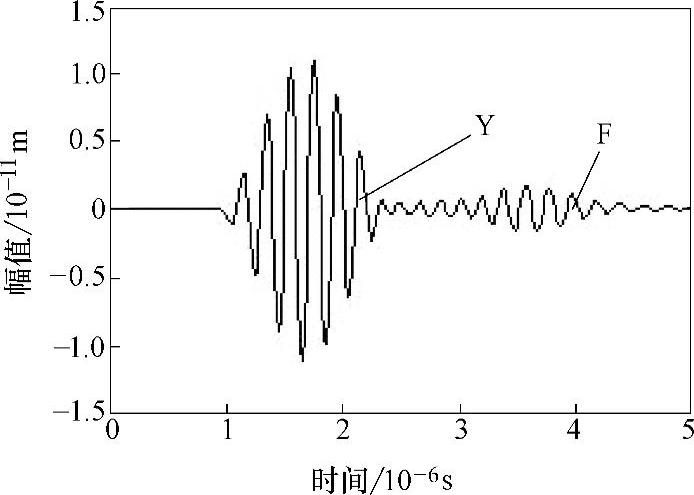
图2-41 y=17mm处的A扫描信号图

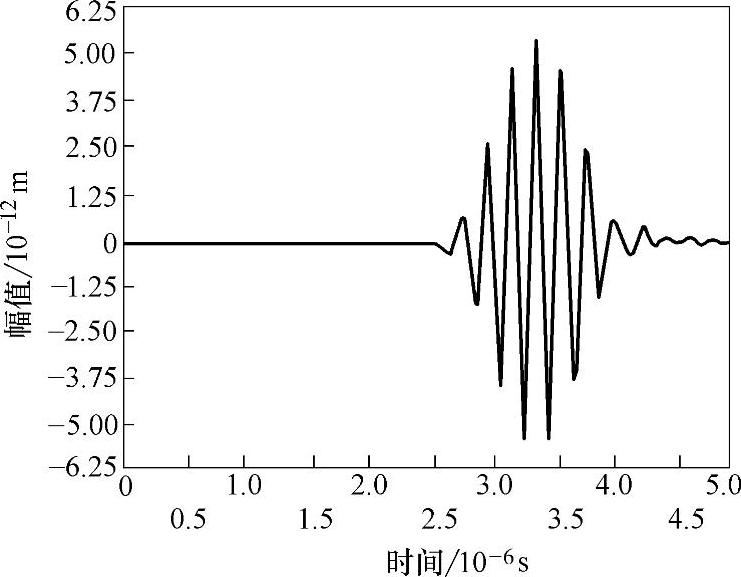
图2-42 y=3mm处经Al₂O₃夹杂物散射的A扫描信号图

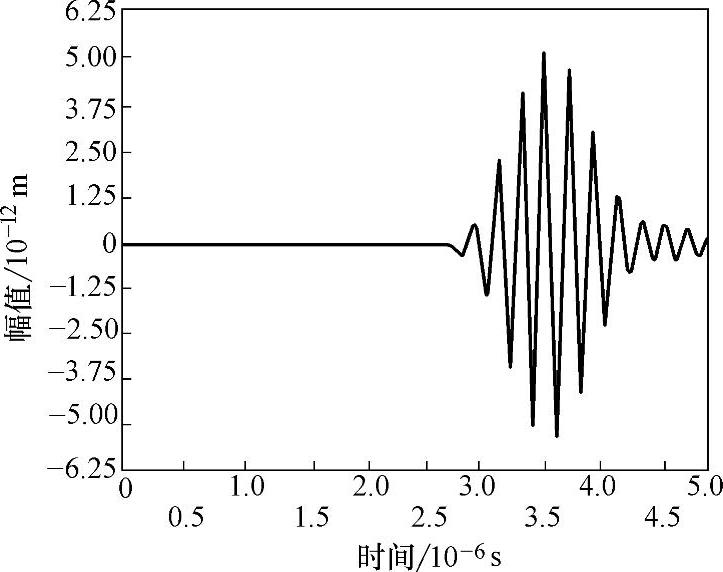
图2-43 y=3mm处经MnS夹杂物散射的A扫描信号图