以上推导得出式（2-49）、式（2-53）表示的是人工截断边界面上的应力分布，是一种连续分布的应力边界条件。采用有限元法模拟固体中超声波传播过程时，应力边界面将被离散化，式（2-49）、式（2-53）可以写成统一的离散形式

式中，s表示节点编号，j表示分量方向，k_sj、c_sj分别表示节点s、方向j的应力表达式中对应的常数。

由式（2-54）可以看出，人工边界面上某一节点某一方向的应力仅与该节点的位移和速度有关，应力边界条件在时域内是时空解耦的，形式简单，计算量小。该应力边界的实现可以采用有限元分析中的弹簧-阻尼单元来实现，该单元的一端与人工边界面节点相连，一端固定。具体的实施方法^[142]如图2-2所示，图中p、q沿人工边界面的切向，r沿人工边界面的法向。图中人工边界面上的弹簧、阻尼参数为

切向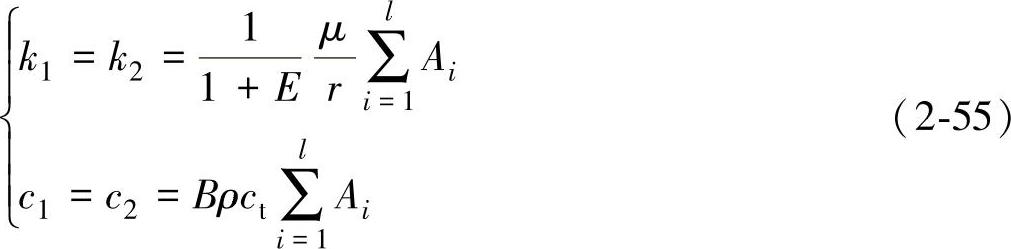

法向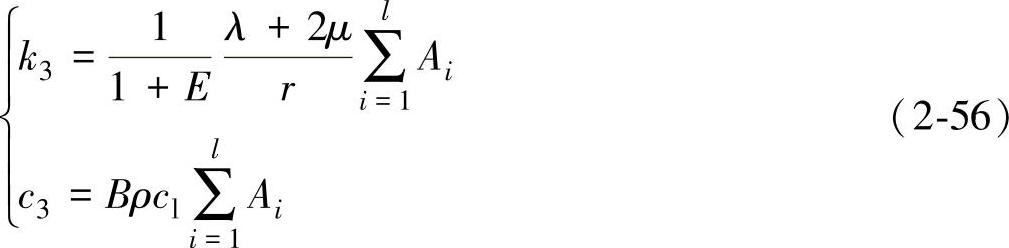

式中，E为无量纲参数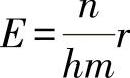，；r为散射源点到边界面的最短距离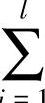；A_i为人工边界面上节点应力影响的范围，A_i=A/D，A为人工截断边界上网格单元的面积，D为网格单元包含的节点数，l为与节点相关的单元数量，图2-2中D=4，l=4；B表示物理波速与视波速的关系，反映多个不同角度折射平面子波的平均速度。参数E、B的取值可通过数值实验获得，E=0.78，B=1.07为实验获得的较优值。

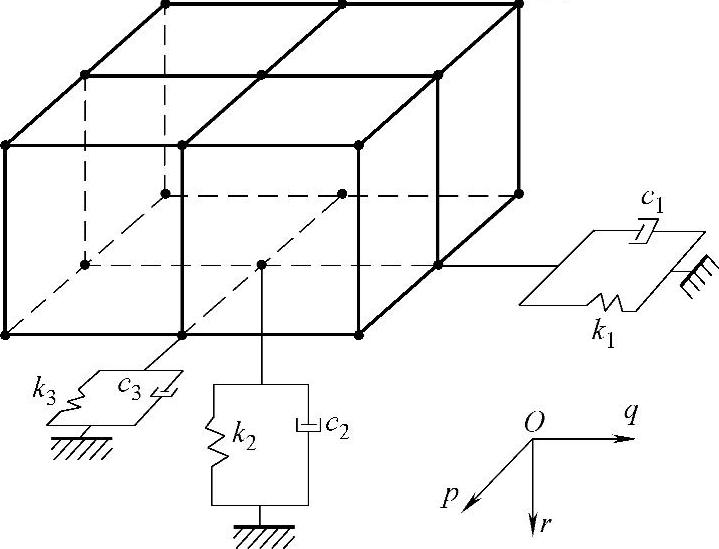
图2-2 三维应力人工边界示意图

算例：随时间变化的均布荷作用下弹性半空间平面问题瞬态动力学分析(www.daowen.com)

从半空间无限域取一4m×2m的矩形平面结构（见图2-3），顶部中间一定范围内受随时间变化的均布荷载，载荷作用跨度为2m，荷载如下

材料弹性模量E=2×10¹¹Pa，泊松比0.3，密度为7800kg/m³，网格尺寸0.1m×0.1m，时间步长为0.02s，上边界为自由边界，其余边界处施加应力人工边界条件，求载荷作用中心点P（0，0）在y方向的位移响应。

图2-4所示是P点位移的数值精确解与本书应力边界解、文献[141]的黏性边界解、文献[142]的黏弹性边界解进行比较的结果。从图中可以看出，黏性边界出现了飘移失稳显现，黏弹性边界条件和本书的应力边界条件是稳定的。原因在于黏性边界的力学模型为悬浮在空中的脱离体，在交变载荷作用下发生了飘移失稳；黏弹性边界条件以及本书采用的应力边界条件力学模型为两端固定的弹簧-阻尼单元，因此在交变载荷作用下，数值求解过程是稳定的。相比于黏弹性边界条件，本书采用的应力边界条件通过对弹簧-阻尼参数进行优化，计算精度进一步提高。

图2-3 弹性半空间平面问题力学模型

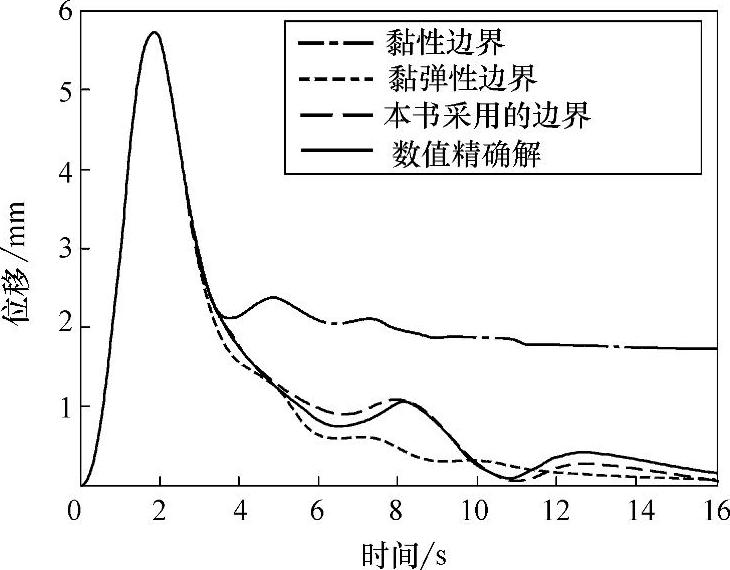
图2-4 不同边界条件下P点位移的计算结果