1.人工边界外行波的假定

在超声检测中，常常运用的是超声波的定向传播特性，因此采用多个考虑远场几何衰减的平面波与不同角度折射的平面波组成的人工边界外行折射波^[141]，沿着人工边界法向传播时，其位移可表示为

式中，第一项表示m个以速度c_i沿人工边界外法向（r方向）传播的远场散射平面波，R为远场几何数衰减函数，三维时R=1/r，二维时R=1/r，h为量纲协调因子，g_i（x）为第i个子波的波形函数；第二项表示n个以速度c_j沿人工边界外法向（r方向）传播的平面波，g_j（x）为第j个子波的波形函数。

假定各子波的波动形式相同（波形函数为g），各子波的传播速度统一用c近似代替，式（2-44）简化为

u（r，t）=（hmf+n）g（ct-r） （2-45）

2.三维法向边界应力条件

平面纵波垂直人工边界向无限域传播时，ϕ≠0，ψ_p=ψ_q=0，u_l表示纵波位移，由式（2-42）、式（2-43）可得法向边界面应力为

将式（2-45）带入式（2-46）整理可得

由式（2-45）、式（2-47）可以建立正应力和位移之间的关系为

由于纵波速度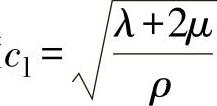，所以式（2-48）简化为(www.daowen.com)

由式（2-49）可知，人工边界面正应力是法向位移与法向速度的函数。

3.三维切向边界应力条件

平面横波垂直人工边界向无限域传播，计算τ_rq时，ϕ=0，ψ_p≠0，ψ_q=ψ_r=0，计算τ_rp时，ϕ=0，ψ_q≠0，ψ_p=ψ_r=0，u_t表示横波位移，由式（2-42）、式（2-43）可得人工边界面剪应力为

将式（2-45）带入式（2-50）整理可得

由式（2-45）、式（2-51）可以建立剪应力和位移之间的关系为

由于横波速度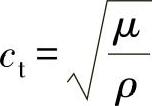，所以式（2-52）简化为

由式（2-53）可知，人工边界面剪应力也是切向位移与切向速度的函数。

二维应力边界的推导同上，不同之处在于二维时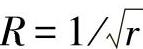，三维时R=1/r。由于势函数可以用统一的形式表示不同波形的波动方程，所以其他形式的人工边界外形波应力边界的推导过程完全相同。