由于超声波在弹性介质（固体）中的传播实质上是弹性介质中各质点在相互关联的弹性介质力作用下依次产生的振动。在检测中，作为声源的探头是首先激发固体中质点振动的外力，而质点一有振动就意味着质点的位移，有位移就会产生应力，因此，寻找固体中应力、位移与超声波波动方程的关系，就可以建立应力人工边界条件。

各向同性弹性固体介质内部（不包括边界），超声波可以有两种传播方式，即质点的振动方向与传播方向一致的纵波，质点的振动方向与传播方向垂直的横波。当固体介质的体积发生交替变化时产生纵波，由于固体介质除了能承受体积变形之外，还能承受切变变形，因此，当有剪切力交替作用于固体介质时产生横波。此时作用于固体介质内部的应力，其大小与分布同时满足弹性固体介质的本构关系和超声波传播的波动方程。

三维无限域弹性固体介质中，由介质本构关系得到应力-位移关系的张量表达式为

σ_ij=λu_k，kδ_ij+μ（u_i，j+u_j，i） （2-40）

式中，σ_ij为应力分量；λ、μ为介质拉梅常数；i、j、k为二维张量下标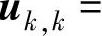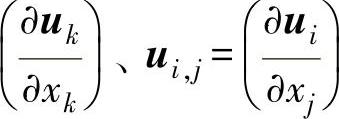；为应变分量；δ_ij为克罗内克符号，δ_ij=1（i=j），δ_ij=0（i≠j）。

固体弹性介质中超声波的波动方程式（2-1）可用势函数表示为

式中，Φ为势函数，表示相对于纵波的位移势ϕ或者相对于横波的位移势ψ_i（i=p，q，r）；c为波速。

势函数与位移之间的关系定义为(www.daowen.com)

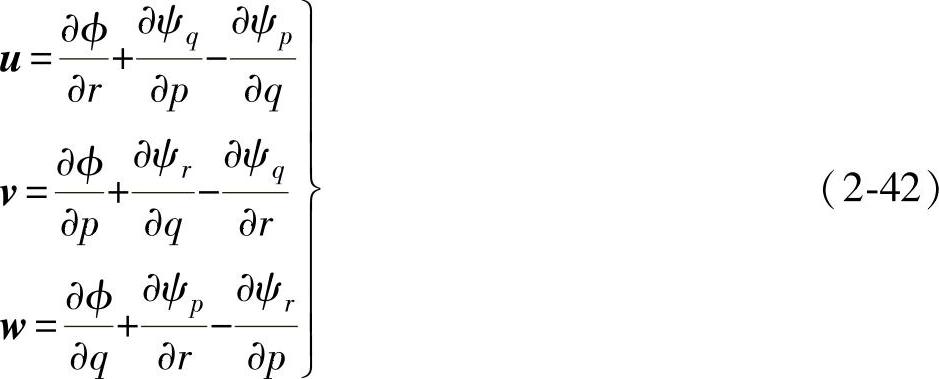
式中，u、v、w分别表示r、p、q方向的位移。

图2-1所示为从半无限区域截取的一个矩形区域，（p，q，r）为人工截断边界面上的坐标系，r为边界面的外法线方向，p，q平行于边界面。人工截断边界面为固体与空气的交界面，由于在空气中检测用的超声波传播极其微弱，所以垂直于界面的正应力和平行于界面的剪应力都等于0，当超声波传播到人工截断边界之后，必然会产生反射现象。反之，如果能够计算出满足式（2-40）、式（2-41）、式（2-42）的固体内任一点的正应力及剪应力，并将其添加在人工截断边界上，就可以使超声波在人工边界处的传播特性与原连续介质一致，不会发生反射现象。

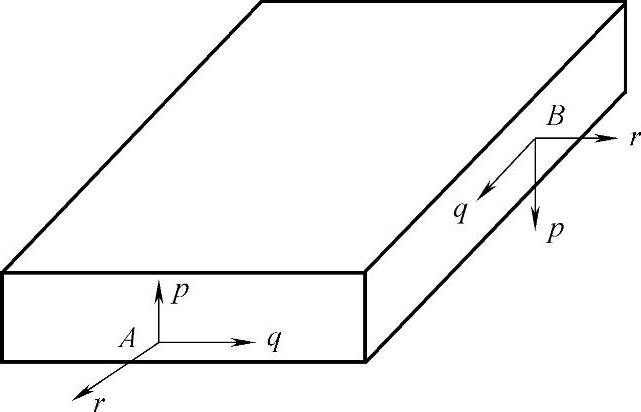
图2-1 人工截断边界面上的坐标系

由式（2-40）、式（2-41）、式（2-42）可以推导出超声波传播时，固体内任一点的应力为

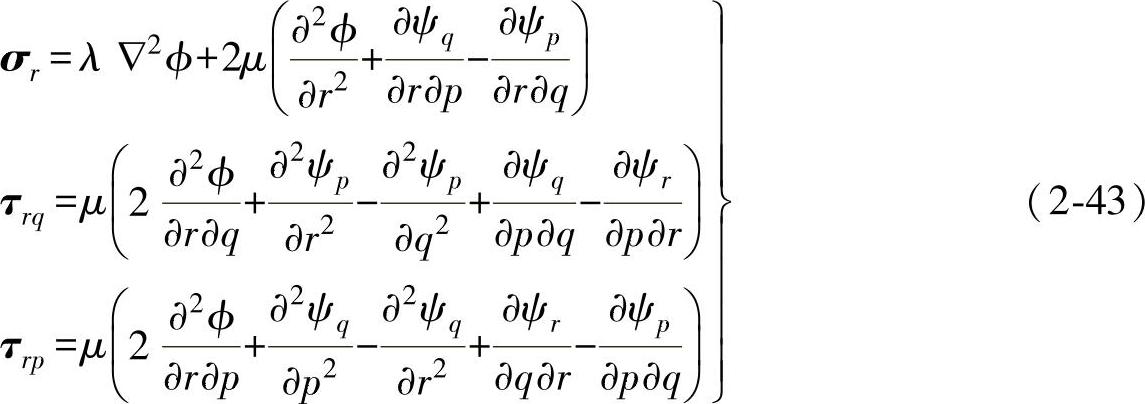
式中，σ_r为正应力；τ_rq、τ_rp为剪应力，ϕ、ψ_i（i=r，p，q）分别表示纵波位移势函数与横波位移势函数，因此当选定波形（如平面波、球面波、柱面波等）之后，就可以计算出具体的应力值。