1.波动方程有限元公式求解

目前求解式（2-18）的方法有直接法和振动叠加法两类，直接积分法又包括中心差分法和NewmarK积分法，其中NewmarK积分法是著名的有限元分析软件ANSYS求解动力学问题的方法，利用NewmarK积分法求解波动方程的算法如下。

（1）初始计算

1）通过对求解区域离散化、单元分析、整体分析，把变分问题近似表达成线性方程组，从而形成系统的刚度矩阵K、质量矩阵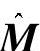和阻尼矩阵C（如果忽略阻尼的影响，则C=0）。

2）给定。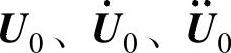

3）选择时间步长Δt、参数α和δ，并计算积分常数。

4）形成有效刚度矩阵元：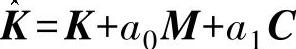

5）三角分解元：

（2）对于每一时间步长，计算t+Δt时刻作用在系统上的有效载荷

求解t+Δt时刻的位移

求解t+Δt时刻的加速度和速度

根据式（2-22）求得位移向量U（t），进而可求得相应的应变ε（t）和应力σ（t）。

2.波动方程有限元公式求解稳定性探讨

式（2-18）可用与其等价的n个形式相同、不相耦合的微分方程组表示，因此只需讨论该方程组中任意一个方程的稳定性即可，该方程可表示为

由于稳定性讨论的是初始条件或边界条件做微小变动时，方程解的变动情况，因此可令f_i=0，式（2-23）简化为

假设时间步长为Δt，采用NewmarK积分法求解式（2-18），得到如下表达式

将式（2-25）代入式（2-24），可以得到

利用NewmarK积分法，根据式（2-24），将式（2-26）改写为(www.daowen.com)

利用式（2-27）和式（2-24），可将式（2-26）改写为

（2-28）

式中

p_i=Δt²ω²_i （2-29）

假设方程（2-28）的解具有如下形式

（u_i）t+Δt=λ（u_i）t，（u_i）t=λ（u_i）t-Δ_t （2-30）

代入式（2-28），得到关于λ的特征方程

该方程（2-31）的特征值为

其中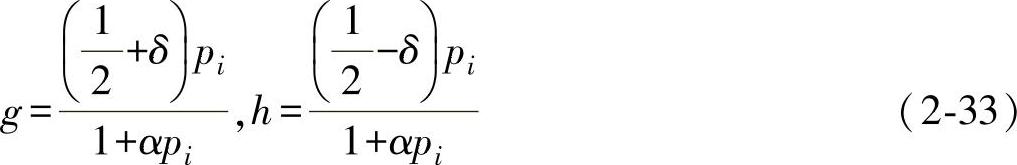

方程的解稳定必须满足两个条件：

1）小阻尼情况下具有振荡的特性，即特征根λ_1，2应当为复数，即

4（1+h）²>（2-g）² （2-34）

将式（2-33）代入式（2-34）得

要使式（2-35）在p_i很大时仍然能成立，则

2）绝对值应当是有限大小的，即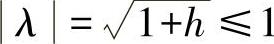，要使式（2-35）在p_i很大时仍然能成立，则

δ≥0.5

当式（2-36）成立时，式（2-37）恒成立，因此综合以上分析过程，NewmarK积分法无条件稳定的条件是