超声检测过程中，探头向介质发射超声波，从而使机械振动在介质内部质点间由近及远相继连续发生而形成应力波的传播。用有限元法分析超声波传播过程中固体介质内部的应力、变形及运动状态等，需要将固体介质离散成若干个单元，进行单元分析和整体分析，得到有限元计算公式。

因为质点位移是空间坐标的函数，所以位移分量u_i可以表示为

u_i（x₁，x₂，x₃）=N^TU_i=NU^T_i （2-13）

N_x1、N_x2、N_x3为x₁、x₂、x₃方向的节点数，N为形函数向量。

N=N（x₃）ⓍN（x₂）ⓍN（x₁）

N（x_i）=（N₁（x_i），N₂（x_i），…，N_Nxi（x_i））T （2-14）

式中，符号⊗表示矩阵的直积。当采用三线性插值函数时，形函数可表示为

将式（2-13）代入式（2-12）得(www.daowen.com)

以矩阵形式改写式（2-16）得

式中，

式中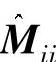，、Kgh分别为分块矩阵。

由于式（2-17）中的δU是任意的，因此可以推导出波动方程的有限元方程

式中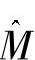，、K分别为系统的质量矩阵、刚度矩阵；F为节点载荷向量，超声检测中，F代表探头的激励载荷。

由以上推导过程可以看出式（2-18）与波动方程式（2-1）是等价的，很显然，通过离散得到的有限元方程式（2-18）要比波动方程式（2-1）容易求解，因此可以通过求解有限元方程得到波动方程的解。